山东省滕州市洪绪中学 北师大版七年级数学下册 5.5利用三角形全等测距离课件(共20张PPT)
文档属性
| 名称 | 山东省滕州市洪绪中学 北师大版七年级数学下册 5.5利用三角形全等测距离课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 14:41:14 | ||
图片预览








文档简介
(共20张PPT)
北师大版七年级数学(下)
山东省滕州市洪绪中学
利用三角形全等测距离
温故而知新
1、三角形全等的判别条件有哪些?
SSS;ASA;AAS;SAS
2、全等三角形的性质有哪些?
对应边相等,对应角相等
学习目标:
1、能利用三角形的全等解决实际问题,体会数学源于生活,服务于生活.
2、能在解决问题的过程中进行有条理的思考和表达.
王老师在游览龙泉广场时,看到了一个美丽的池塘
,我想知道最远两点A、B之间的距离,但是我没有船,不能直接去测量.
手里只有一根绳子和一把尺子,我怎样才能测出A、B之间的距离呢?
想一想
A、B间有多远呢?
A
B
·
·
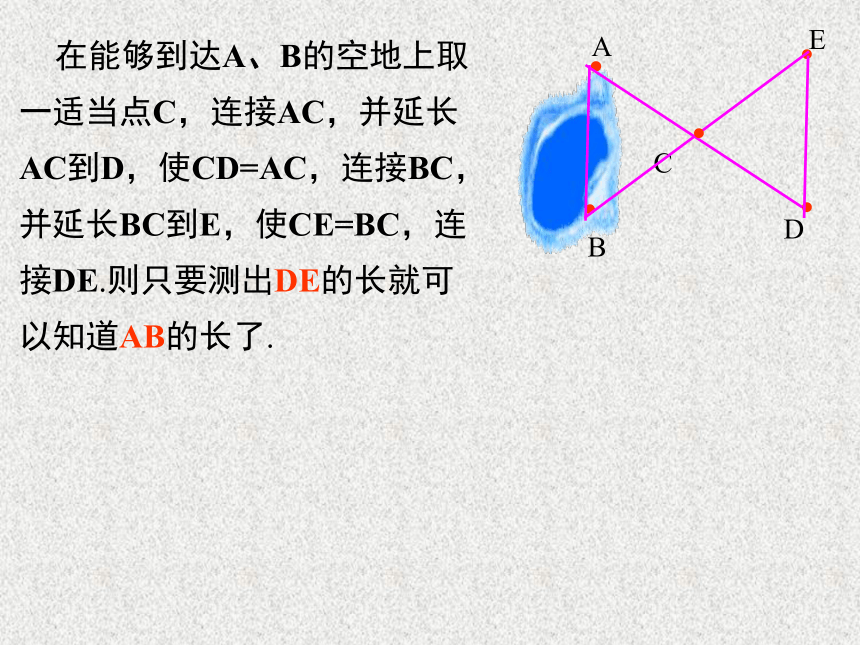
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接DE.则只要测出DE的长就可以知道AB的长了.
·
C
B
A
·
·
·
·
D
E
B
A
·
·
你还有其它的方案吗?独立思考,画出设计图;小组讨论,交流.展示方案.
议一议
∠ABE=∠
DCE=90°
BC=EC
∠AEB=∠DEC
在△ABE和△DCE中
在AB的垂线BF上取两点E,C,使BE=CE,过点C作出BF的垂线段DC,使A,E,D在一条直线上,这时测得DC的长是A,B间的距离.
∴△ABE≌△DCE(ASA)
∴AB=DC
·
D
C
B
A
E
方案
·
·
·
·
F
好高的龙泉塔呀!相当于几层楼高呢?
比一比
想到办法了,要站在塔与楼正中间.
我在干嘛呢?
O
我知道了,相当于14层楼高.
你能用所学的知识说说这样做的理由吗?
A
B
C
D
在抗日战争期间,
为了炸毁与我军阵地隔河
相望的日本鬼子的碉堡,需要
测出我军阵地到鬼子碉堡的距离.
由于没有任何测量工具,我八路军战士
为此绞尽脑汁,这时一位聪明的八路军战士
想出了一个办法,为成功炸毁碉堡立了一功.
议一议
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
A
C
B
D
?
你觉得他测得的距离准确吗?说明其中的理由。
∴BC=
DC(
)
A
C
B
D
?
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
∴△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
如图要测量河两岸相对的两点A、B的距离,先在AB
的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是(
)
A、SSS
B、ASA
C、AAS
D、SAS
B
A
●
●
D
C
E
F
B
做一做
2.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO
应满足下列的哪个条件?(
)
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
D
O
D
C
B
A
课堂小结
1、知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2、方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
一分耕耘,
一分收获.
方案2:作BC边的中线AO,
则
△AOB≌
△AOC(SSS)
方案1:作∠BAC角平分线AD,则△BAD≌
△CAD(SAS)
A
B
C
D
A
B
C
O
3.
1.
SAS
AB
2.
∠CDE
ASA
当堂达标
北师大版七年级数学(下)
山东省滕州市洪绪中学
利用三角形全等测距离
温故而知新
1、三角形全等的判别条件有哪些?
SSS;ASA;AAS;SAS
2、全等三角形的性质有哪些?
对应边相等,对应角相等
学习目标:
1、能利用三角形的全等解决实际问题,体会数学源于生活,服务于生活.
2、能在解决问题的过程中进行有条理的思考和表达.
王老师在游览龙泉广场时,看到了一个美丽的池塘
,我想知道最远两点A、B之间的距离,但是我没有船,不能直接去测量.
手里只有一根绳子和一把尺子,我怎样才能测出A、B之间的距离呢?
想一想
A、B间有多远呢?
A
B
·
·
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接DE.则只要测出DE的长就可以知道AB的长了.
·
C
B
A
·
·
·
·
D
E
B
A
·
·
你还有其它的方案吗?独立思考,画出设计图;小组讨论,交流.展示方案.
议一议
∠ABE=∠
DCE=90°
BC=EC
∠AEB=∠DEC
在△ABE和△DCE中
在AB的垂线BF上取两点E,C,使BE=CE,过点C作出BF的垂线段DC,使A,E,D在一条直线上,这时测得DC的长是A,B间的距离.
∴△ABE≌△DCE(ASA)
∴AB=DC
·
D
C
B
A
E
方案
·
·
·
·
F
好高的龙泉塔呀!相当于几层楼高呢?
比一比
想到办法了,要站在塔与楼正中间.
我在干嘛呢?
O
我知道了,相当于14层楼高.
你能用所学的知识说说这样做的理由吗?
A
B
C
D
在抗日战争期间,
为了炸毁与我军阵地隔河
相望的日本鬼子的碉堡,需要
测出我军阵地到鬼子碉堡的距离.
由于没有任何测量工具,我八路军战士
为此绞尽脑汁,这时一位聪明的八路军战士
想出了一个办法,为成功炸毁碉堡立了一功.
议一议
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
A
C
B
D
?
你觉得他测得的距离准确吗?说明其中的理由。
∴BC=
DC(
)
A
C
B
D
?
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
∴△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
碉堡距离
如图要测量河两岸相对的两点A、B的距离,先在AB
的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是(
)
A、SSS
B、ASA
C、AAS
D、SAS
B
A
●
●
D
C
E
F
B
做一做
2.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO
应满足下列的哪个条件?(
)
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
D
O
D
C
B
A
课堂小结
1、知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2、方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
一分耕耘,
一分收获.
方案2:作BC边的中线AO,
则
△AOB≌
△AOC(SSS)
方案1:作∠BAC角平分线AD,则△BAD≌
△CAD(SAS)
A
B
C
D
A
B
C
O
3.
1.
SAS
AB
2.
∠CDE
ASA
当堂达标
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
