人教版八年级下册数学19.2一次函数课件(共14张PPT)
文档属性
| 名称 | 人教版八年级下册数学19.2一次函数课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 265.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 15:27:35 | ||
图片预览



文档简介
(共14张PPT)
一次函数
导入新课
我们前面学习了有关一次函数的一些知识及如何确定解析式,如何利用一次函数知识解决相关实践问题呢?
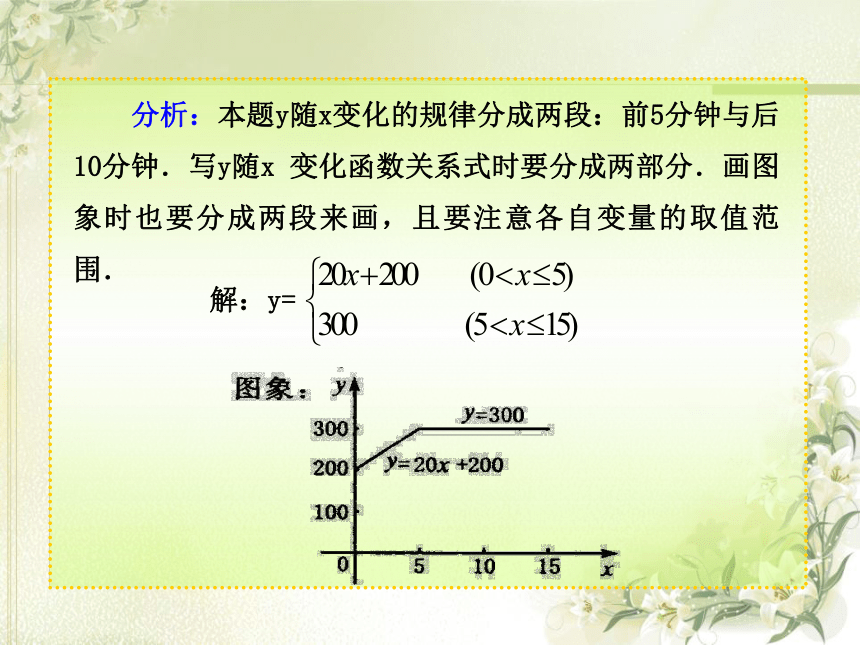
小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟.试写出这段时间里她跑步速度y(米/分)随跑步时间x(分)变化的函数关系式,并画出图象.
分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.
解:y=
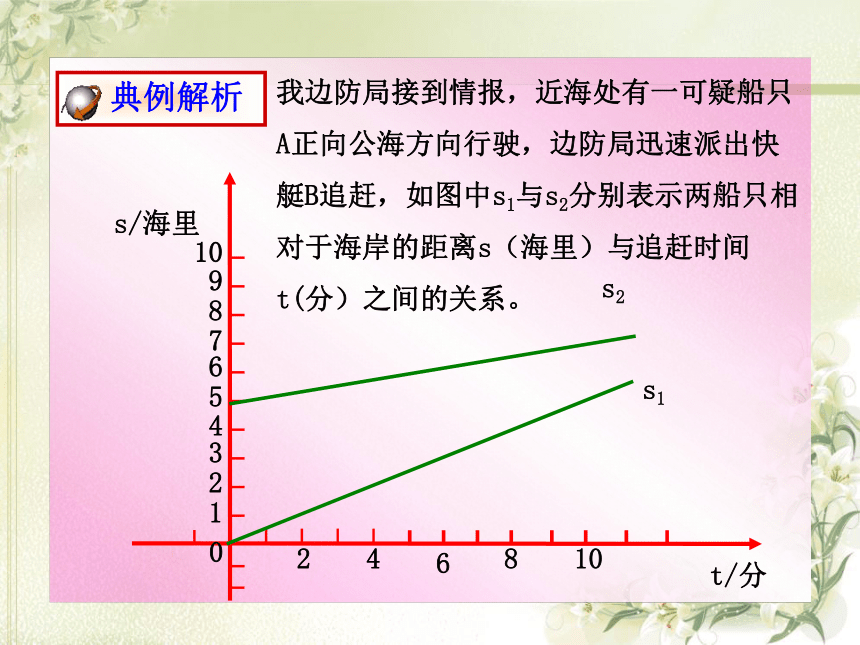
我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,如图中s1与s2分别表示两船只相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。
2
1
4
3
6
5
8
7
10
9
2
4
6
0
8
10
s1
s2
t/分
s/海里
典例解析
2
1
4
3
6
5
8
7
10
9
t/分
s/海里
2
4
6
0
8
10
s1
s2
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A,B哪个速度快?
当t=0时,s=0,所以s1表示B到海岸的距离与追赶时间之间的关系.
B
A
B的速度快
2
4
6
8
10
t/分
s/海里
2
4
6
0
8
10
s1
s2
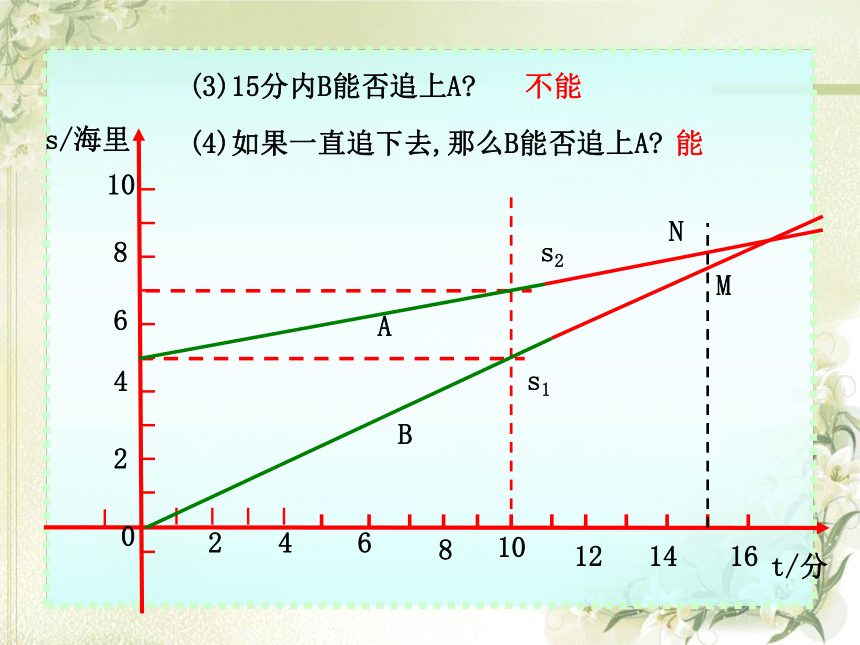
(3)15分内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
12
14
16
M
N
A
B
不能
能
2
4
6
8
10
t/分
s/海里
2
4
6
0
8
10
s1
s2
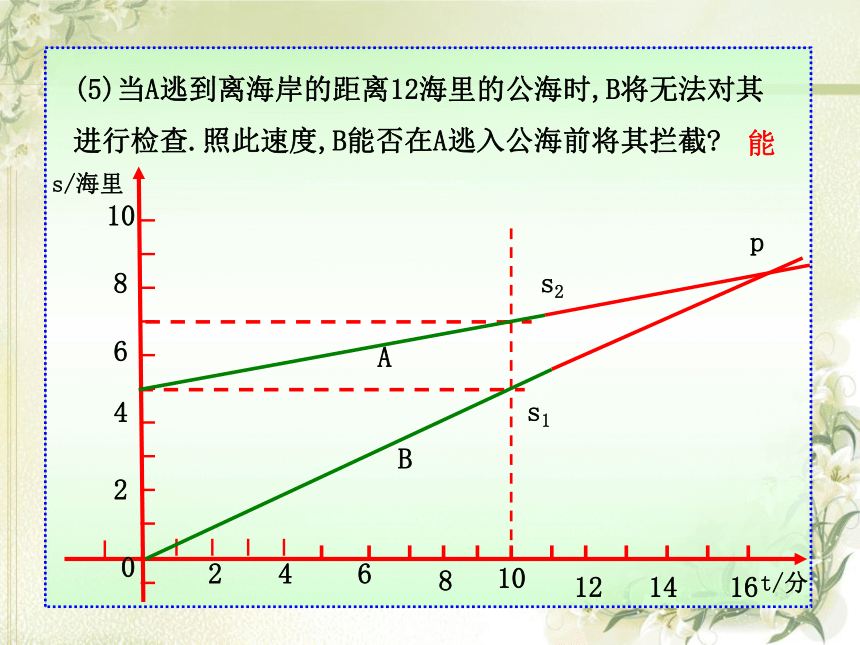
(5)当A逃到离海岸的距离12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
12
p
14
16
B
A
能
合作探究
A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡.从A城往C、D两乡运肥料费用分别为每吨20元和25元;从B城往C、D两乡运肥料费用分别为每吨15元和24元.现C乡需要肥料240吨,D乡需要肥料260吨.怎样调运总运费最少?
通过分析思考,可以发现:A──C,A──D,B──C,B──D运肥料共涉及4个变量.它们都是影响总运费的变量.然而它们之间又有一定的必然联系,只要确定其中一个量,其余三个量也就随之确定.
若设A──Cx吨,则:
由于A城有肥料200吨:A─D,200─x吨.
由于C乡需要240吨:B─C,240─x吨.
由于D乡需要260吨:B─D,260─200+x吨.
那么,各运输费用为:
A──C
20x
A──D
25(200-x)
B──C
15(240-x)
B──D
24(60+x)
解:设总运输费用为y的话,y与x关系为:
y=20x+25(200-x)+15(240-x)+24(60+x)
即:y=4x+10040
(0≤x≤200)
由解析式或图象都可看出,
当x=0时,y值最小为10040.
因此,从A城运往C乡0吨,运往D乡200吨;从B城运往C乡240吨,运往D乡60吨.此时总运费最少,为10040元.
巩固训练
如图,y1反映了某公司产品的销售收入与销售量之间的关系,y2反映了该公司产品的销售成本与销售量之间的关系,根据图意填空:
X吨
0
1
2
3
4
5
6
7
8
6000
1000
2000
3000
4000
5000
(1)当销售量为2吨时,
销售收入=______元,
销售成本=_____元;
(2)当销售量为5吨时,
销售收入=_________元,销售成本=________元;
y1
y2
Y元
2000
3000
5000
6000
X吨
0
1
2
3
4
5
6
7
8
6000
1000
2000
3000
4000
5000
(3)当销售量等于_______时,销售收入等于销售成本;
(4)当销售量_________时,该公司赢利(收入大于成本);当销售量_________时,该公司亏损(收入小于成本)
y1
y2
y1对应的函数表达式是____________
y2对应的函数表达式是____________
4吨
大于4吨
小于4吨
y1=1000x
y2=500x+2000
1.能通过函数图象获取信息,发展形象思维。
2.能利用函数图象解决简单的实际问题,发展数学的应用能力。
通过这节课的学习你能做到吗?
谈谈你的收获
一次函数
导入新课
我们前面学习了有关一次函数的一些知识及如何确定解析式,如何利用一次函数知识解决相关实践问题呢?
小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟.试写出这段时间里她跑步速度y(米/分)随跑步时间x(分)变化的函数关系式,并画出图象.
分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.
解:y=
我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,如图中s1与s2分别表示两船只相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。
2
1
4
3
6
5
8
7
10
9
2
4
6
0
8
10
s1
s2
t/分
s/海里
典例解析
2
1
4
3
6
5
8
7
10
9
t/分
s/海里
2
4
6
0
8
10
s1
s2
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A,B哪个速度快?
当t=0时,s=0,所以s1表示B到海岸的距离与追赶时间之间的关系.
B
A
B的速度快
2
4
6
8
10
t/分
s/海里
2
4
6
0
8
10
s1
s2
(3)15分内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
12
14
16
M
N
A
B
不能
能
2
4
6
8
10
t/分
s/海里
2
4
6
0
8
10
s1
s2
(5)当A逃到离海岸的距离12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
12
p
14
16
B
A
能
合作探究
A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡.从A城往C、D两乡运肥料费用分别为每吨20元和25元;从B城往C、D两乡运肥料费用分别为每吨15元和24元.现C乡需要肥料240吨,D乡需要肥料260吨.怎样调运总运费最少?
通过分析思考,可以发现:A──C,A──D,B──C,B──D运肥料共涉及4个变量.它们都是影响总运费的变量.然而它们之间又有一定的必然联系,只要确定其中一个量,其余三个量也就随之确定.
若设A──Cx吨,则:
由于A城有肥料200吨:A─D,200─x吨.
由于C乡需要240吨:B─C,240─x吨.
由于D乡需要260吨:B─D,260─200+x吨.
那么,各运输费用为:
A──C
20x
A──D
25(200-x)
B──C
15(240-x)
B──D
24(60+x)
解:设总运输费用为y的话,y与x关系为:
y=20x+25(200-x)+15(240-x)+24(60+x)
即:y=4x+10040
(0≤x≤200)
由解析式或图象都可看出,
当x=0时,y值最小为10040.
因此,从A城运往C乡0吨,运往D乡200吨;从B城运往C乡240吨,运往D乡60吨.此时总运费最少,为10040元.
巩固训练
如图,y1反映了某公司产品的销售收入与销售量之间的关系,y2反映了该公司产品的销售成本与销售量之间的关系,根据图意填空:
X吨
0
1
2
3
4
5
6
7
8
6000
1000
2000
3000
4000
5000
(1)当销售量为2吨时,
销售收入=______元,
销售成本=_____元;
(2)当销售量为5吨时,
销售收入=_________元,销售成本=________元;
y1
y2
Y元
2000
3000
5000
6000
X吨
0
1
2
3
4
5
6
7
8
6000
1000
2000
3000
4000
5000
(3)当销售量等于_______时,销售收入等于销售成本;
(4)当销售量_________时,该公司赢利(收入大于成本);当销售量_________时,该公司亏损(收入小于成本)
y1
y2
y1对应的函数表达式是____________
y2对应的函数表达式是____________
4吨
大于4吨
小于4吨
y1=1000x
y2=500x+2000
1.能通过函数图象获取信息,发展形象思维。
2.能利用函数图象解决简单的实际问题,发展数学的应用能力。
通过这节课的学习你能做到吗?
谈谈你的收获
