9.2 实际问题与一元一次不等式(1)
文档属性
| 名称 | 9.2 实际问题与一元一次不等式(1) |  | |
| 格式 | rar | ||
| 文件大小 | 328.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-25 12:35:40 | ||
图片预览





文档简介
(共22张PPT)
福渡初级中学
2、某产品进价120元,共有15件,为了使利润不低于1000元,那么这件产品的定价至少在多少元?
(x-120)×15≥1000
1、某商品的单价为a元,买50件这样的商品的总费用不高于342元,则商品的单价至多为多少元?
解: 50a≤342
解:设定价至少为x元
门票70元/人,团体优惠
欢迎
光临
两名老师全额付款,其余的人五五折(按报价的55%)
所有的人六折收费
(按报价的60%)
甲经理
乙经理
选择哪个提议更实惠?
东湖
两名老师全额付款,其余的人五五折(按报价的55%)
甲经理
乙经理
所有的人六折收费
(按报价的60%)
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = (140+38.5x)元;
选乙经理的建议,则费用为:
(2+x)×70 ×60%=(84+42x)元
1)当甲乙经理的建议的费用一样多
140+38.5x =84+42x时,x=16,
即当学生人数是16时,选择甲乙经理的建议的费用一样多;
门票70元/人,
团体优惠
门票70元,团体优惠
两名老师全额付款,其余的五五折(按报价的55%)
甲经理
乙经理
所有的人八折收费
(按报价的60%)
3)当乙经理的建议更实惠时
140+38.5x >84+42x时,x < 16,
即学生人数小于16时,选择乙经理的建议更实惠.
2)当甲经理的建议更实惠时
140+38.5x <84+42x时,x>16,
即当学生人数大于16时,选择甲经理的建议更实惠;
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = (140+38.5x)(元);
选乙经理的建议,则费用为:
(2+x)×70 ×60%=(84+42x)(元)
甲店
乙店
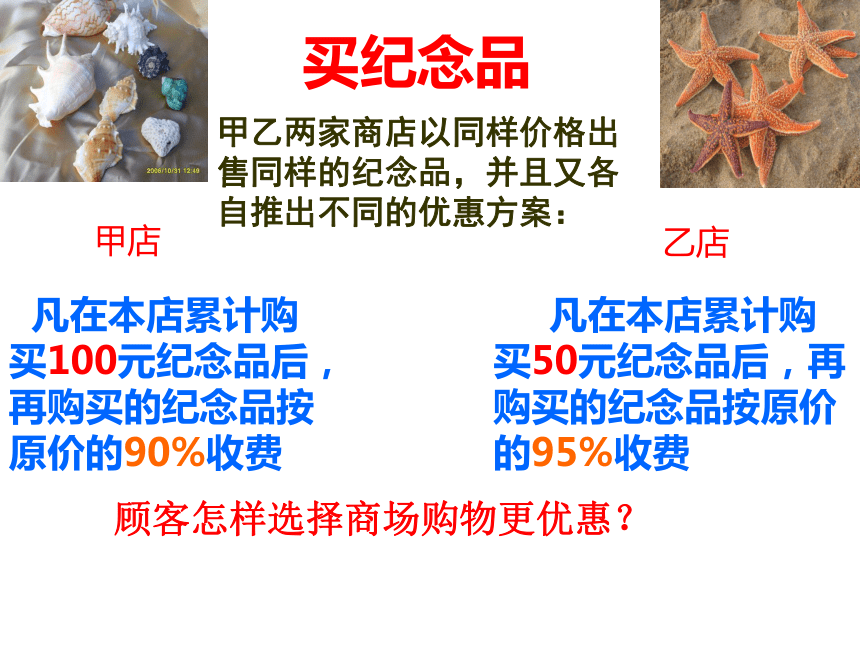
凡在本店累计购买100元纪念品后,再购买的纪念品按原价的90%收费
凡在本店累计购买50元纪念品后,再购买的纪念品按原价的95%收费
甲乙两家商店以同样价格出售同样的纪念品,并且又各自推出不同的优惠方案:
买纪念品
顾客怎样选择商场购物更优惠?
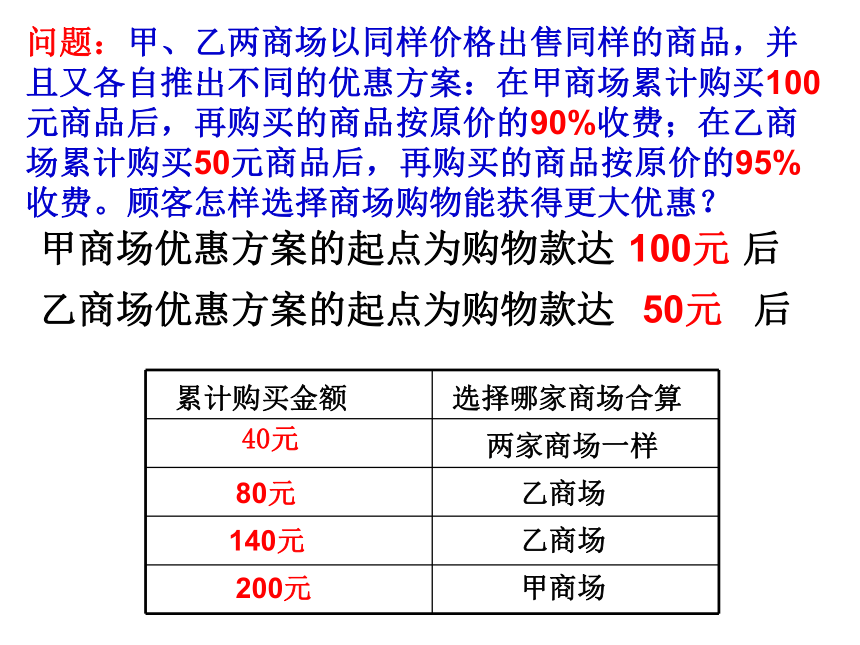
问题:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
甲商场优惠方案的起点为购物款达 后
乙商场优惠方案的起点为购物款达 后
40元
累计购买金额
选择哪家商场合算
两家商场一样
乙商场
140元
200元
80元
甲商场
乙商场
100元
50元
3、如果累计购物超过100元;
(1)什么情况下,在甲商场花费小?
(2)什么情况下,在乙商场花费小?
(3)什么情况下,在两家商场购物花费一样?
在乙商场花费小。
又有三种情况:
甲、乙两商场以同样价格出售同样的商品。并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
分三种情况分析:
设累计购物x元(x>100元)。
则在甲商场的花费为
在乙商场的花费为
1、如果累计购物不超过50元;
在两家商场购物花费时一样的。
2、如果累计购物超过50元但不超过100元时;
设累计购物x元(x>100元)。
则在甲商场的花费为
在甲商场的花费为
(1)如果在甲商场花费小,则
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,累计购物超过150元时在甲商场购物花费小。
(2)累计购物超过100元但小于150元时,
(3)累计购物刚好是150元时,
在乙商场购物花费小.
在两家商场购物花费一样多.
购物金额0< x ≤50元时,在两个店都一样;
购物金额50< x < 150元时,在乙店花费小;
购物金额x= 150元时,在两个店都一样;
购物金额x>150元时,在甲店花费小;
综上所述:
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的不等关系
(2)设:设适当的未知数
(3)列:列不等式
(4)解:求出不等式的解集
(5)答:写出符合题意的答案
运用不等式解决实际问题的基本步骤
娃哈哈矿泉水的
原价都是1元/瓶
抢购
抢购
娃哈哈矿泉水20瓶以上时,超过部分打8折!
某班学生要买矿泉水,该选哪家商店呢?
娃哈哈矿泉水
全部九折!
甲公司
乙公司
(1)当0.9x>20+ (x-20)×0.8时,
设该班要购买x瓶矿泉水,则
(3)当0.9x<20+ (x-20)×0.8时,
即:当x >40时,选择乙公司比较合算。
即:当x < 40时,选择甲公司比较合算。
解:
(2)当0.9x=20+ (x-20)×0.8时,
即:当x =40时,选择甲公司、乙公司一样。
甲公司的费用为: 0.9x元;
乙公司的费用为: [ 20+ (x-20)×0.8 ]元;
问题2:甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元。两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款。某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
问题2:
甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元。两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款。某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
解:设这个顾客购买了x只茶杯,
(1)在甲商店花费小,则有:
分三种情况分析:
则在甲商店需花费
在乙商店需花费
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,当购买34只茶杯以上在乙商店优惠更多.
(2)当购买34只茶杯以下但超过4只时,在甲商店优惠更多.
(3)当购买34只茶杯时,在两家商店获得的优惠一样多.
问题3: 某单位要制作一批宣传材料,甲广告公司提出:每份材料收费50元,另收设计费2000元,乙广告公司提出:每份材料收费70元,不收设计费。
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
作业:
P140 1(2)、(3)、(6);2;3(2)、(4);11;
4.学校为了解决部分学生午餐,联系了两家快餐公司,两家公司的报价、质量和服务承诺都相同,且都表示对学生优惠:甲公司表示每份按报价的九折收费,乙公司表示购买100份以上的部分按报价的八折优惠。问选择哪家公司较好?
作差: y甲 - y乙 = 0.9x – [100+0.8(x-100)] = 0.1x – 20
当0.1x – 20>0时,解得:x>200
当0.1x – 20=0时,解得:x=200
当0.1x – 20<0时,解得:x<200
∴购买盒饭大于200份时,选乙公司;购买200份时,两家一样;购买盒饭小于200份时选甲公司.
解:设购买x份盒饭,每盒饭单价为”1”,则:
y甲= 0.9x; y乙=100 + 0.8(x -100);
应用一元一次不等式解实际问题步骤:
实际问题
建立数学模型
(一元一次不等式)
审题、设未知数
根据不等关系列出不等式
数学问题的解
实际问题的解
检验
解一元一次不等式
去括号
移项
合并
系数化为1
收 获
③我感受最深的是 ………
④我发现了生活中………
②我感到最困难的是………
①我学会了………
我想说:
福渡初级中学
2、某产品进价120元,共有15件,为了使利润不低于1000元,那么这件产品的定价至少在多少元?
(x-120)×15≥1000
1、某商品的单价为a元,买50件这样的商品的总费用不高于342元,则商品的单价至多为多少元?
解: 50a≤342
解:设定价至少为x元
门票70元/人,团体优惠
欢迎
光临
两名老师全额付款,其余的人五五折(按报价的55%)
所有的人六折收费
(按报价的60%)
甲经理
乙经理
选择哪个提议更实惠?
东湖
两名老师全额付款,其余的人五五折(按报价的55%)
甲经理
乙经理
所有的人六折收费
(按报价的60%)
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = (140+38.5x)元;
选乙经理的建议,则费用为:
(2+x)×70 ×60%=(84+42x)元
1)当甲乙经理的建议的费用一样多
140+38.5x =84+42x时,x=16,
即当学生人数是16时,选择甲乙经理的建议的费用一样多;
门票70元/人,
团体优惠
门票70元,团体优惠
两名老师全额付款,其余的五五折(按报价的55%)
甲经理
乙经理
所有的人八折收费
(按报价的60%)
3)当乙经理的建议更实惠时
140+38.5x >84+42x时,x < 16,
即学生人数小于16时,选择乙经理的建议更实惠.
2)当甲经理的建议更实惠时
140+38.5x <84+42x时,x>16,
即当学生人数大于16时,选择甲经理的建议更实惠;
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = (140+38.5x)(元);
选乙经理的建议,则费用为:
(2+x)×70 ×60%=(84+42x)(元)
甲店
乙店
凡在本店累计购买100元纪念品后,再购买的纪念品按原价的90%收费
凡在本店累计购买50元纪念品后,再购买的纪念品按原价的95%收费
甲乙两家商店以同样价格出售同样的纪念品,并且又各自推出不同的优惠方案:
买纪念品
顾客怎样选择商场购物更优惠?
问题:甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
甲商场优惠方案的起点为购物款达 后
乙商场优惠方案的起点为购物款达 后
40元
累计购买金额
选择哪家商场合算
两家商场一样
乙商场
140元
200元
80元
甲商场
乙商场
100元
50元
3、如果累计购物超过100元;
(1)什么情况下,在甲商场花费小?
(2)什么情况下,在乙商场花费小?
(3)什么情况下,在两家商场购物花费一样?
在乙商场花费小。
又有三种情况:
甲、乙两商场以同样价格出售同样的商品。并且又各自推出不同的优惠方案:在甲商场累计购买100元商品后,再购买的商品按原价的90%收费;在乙商场累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商场购物能获得更大优惠?
分三种情况分析:
设累计购物x元(x>100元)。
则在甲商场的花费为
在乙商场的花费为
1、如果累计购物不超过50元;
在两家商场购物花费时一样的。
2、如果累计购物超过50元但不超过100元时;
设累计购物x元(x>100元)。
则在甲商场的花费为
在甲商场的花费为
(1)如果在甲商场花费小,则
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,累计购物超过150元时在甲商场购物花费小。
(2)累计购物超过100元但小于150元时,
(3)累计购物刚好是150元时,
在乙商场购物花费小.
在两家商场购物花费一样多.
购物金额0< x ≤50元时,在两个店都一样;
购物金额50< x < 150元时,在乙店花费小;
购物金额x= 150元时,在两个店都一样;
购物金额x>150元时,在甲店花费小;
综上所述:
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的不等关系
(2)设:设适当的未知数
(3)列:列不等式
(4)解:求出不等式的解集
(5)答:写出符合题意的答案
运用不等式解决实际问题的基本步骤
娃哈哈矿泉水的
原价都是1元/瓶
抢购
抢购
娃哈哈矿泉水20瓶以上时,超过部分打8折!
某班学生要买矿泉水,该选哪家商店呢?
娃哈哈矿泉水
全部九折!
甲公司
乙公司
(1)当0.9x>20+ (x-20)×0.8时,
设该班要购买x瓶矿泉水,则
(3)当0.9x<20+ (x-20)×0.8时,
即:当x >40时,选择乙公司比较合算。
即:当x < 40时,选择甲公司比较合算。
解:
(2)当0.9x=20+ (x-20)×0.8时,
即:当x =40时,选择甲公司、乙公司一样。
甲公司的费用为: 0.9x元;
乙公司的费用为: [ 20+ (x-20)×0.8 ]元;
问题2:甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元。两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款。某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
问题2:
甲、乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元。两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的92%收款。某顾客需购买4只茶壶、若干只(超过4只)茶杯,去哪家商店购买优惠更多?
解:设这个顾客购买了x只茶杯,
(1)在甲商店花费小,则有:
分三种情况分析:
则在甲商店需花费
在乙商店需花费
去括号,得:
移项,得:
合并,得:
系数化为1,得:
这就是说,当购买34只茶杯以上在乙商店优惠更多.
(2)当购买34只茶杯以下但超过4只时,在甲商店优惠更多.
(3)当购买34只茶杯时,在两家商店获得的优惠一样多.
问题3: 某单位要制作一批宣传材料,甲广告公司提出:每份材料收费50元,另收设计费2000元,乙广告公司提出:每份材料收费70元,不收设计费。
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
作业:
P140 1(2)、(3)、(6);2;3(2)、(4);11;
4.学校为了解决部分学生午餐,联系了两家快餐公司,两家公司的报价、质量和服务承诺都相同,且都表示对学生优惠:甲公司表示每份按报价的九折收费,乙公司表示购买100份以上的部分按报价的八折优惠。问选择哪家公司较好?
作差: y甲 - y乙 = 0.9x – [100+0.8(x-100)] = 0.1x – 20
当0.1x – 20>0时,解得:x>200
当0.1x – 20=0时,解得:x=200
当0.1x – 20<0时,解得:x<200
∴购买盒饭大于200份时,选乙公司;购买200份时,两家一样;购买盒饭小于200份时选甲公司.
解:设购买x份盒饭,每盒饭单价为”1”,则:
y甲= 0.9x; y乙=100 + 0.8(x -100);
应用一元一次不等式解实际问题步骤:
实际问题
建立数学模型
(一元一次不等式)
审题、设未知数
根据不等关系列出不等式
数学问题的解
实际问题的解
检验
解一元一次不等式
去括号
移项
合并
系数化为1
收 获
③我感受最深的是 ………
④我发现了生活中………
②我感到最困难的是………
①我学会了………
我想说:
