北师大版九年级下册数学 3.4 圆周角课件 (共21张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 3.4 圆周角课件 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 542.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 14:50:28 | ||
图片预览




文档简介
(共21张PPT)
圆周角(1)
观察思考:
在这个海洋馆里,人们可以通过其中的圆弧形玻璃窗观看窗内的海洋动物.
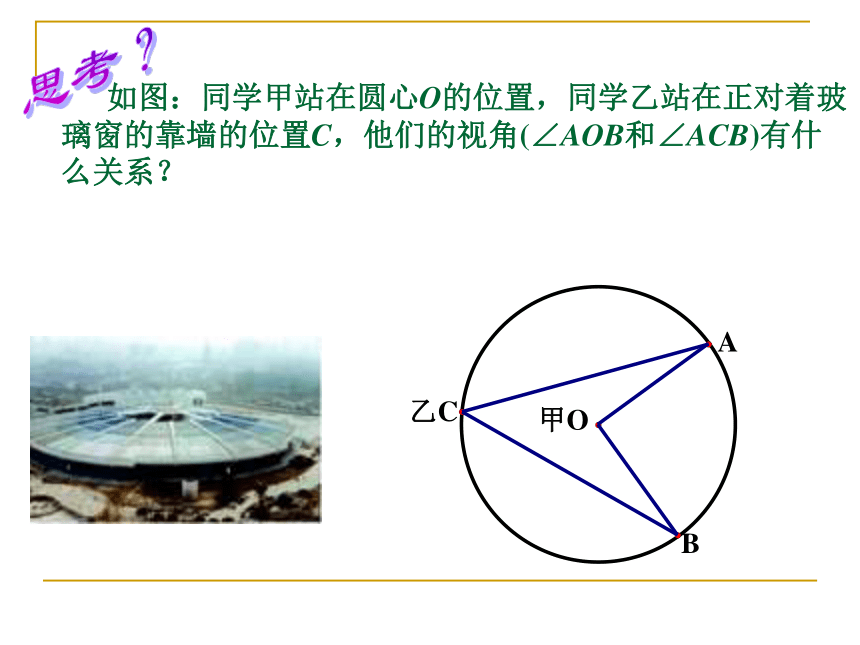
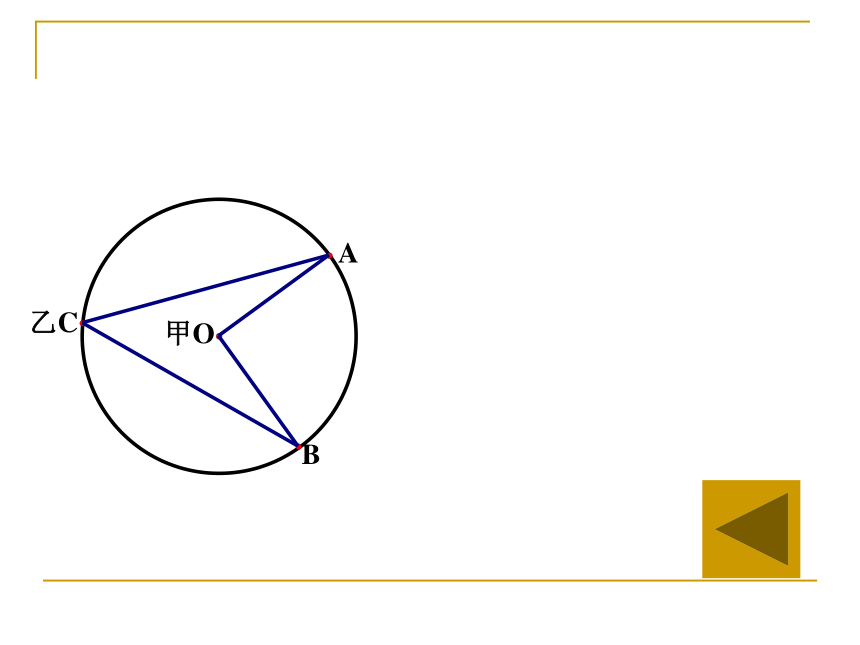
如图:同学甲站在圆心O的位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
思考?
如果同学丙、丁分别站在其他靠墙的位置D和E,
他们的视角(∠ADE和∠AEB)和同学乙的视
角相同吗?
观察:∠C
、∠D、∠E有什么共同的特征?
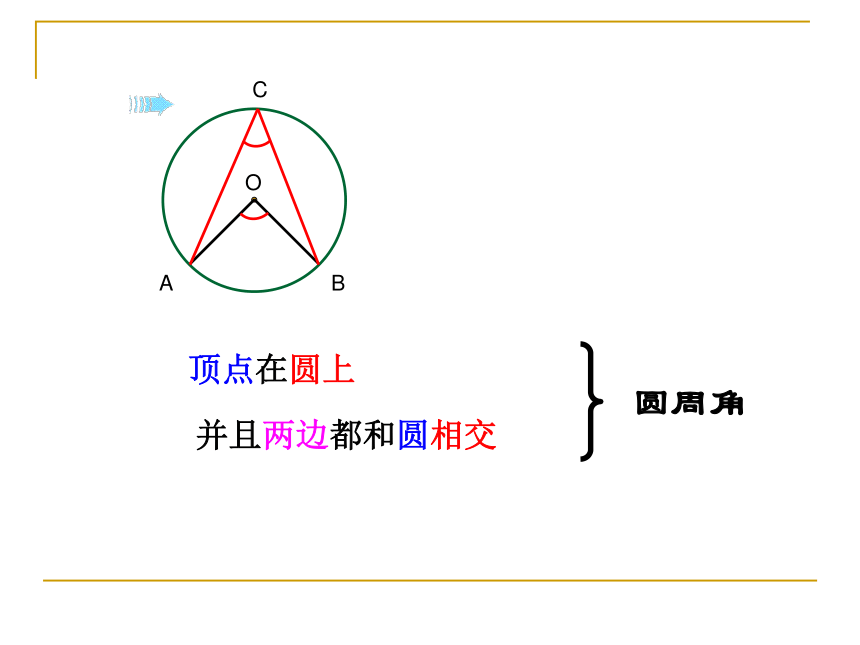
顶点在圆上
并且两边都和圆相交
圆周角
探索:判断下列各图中,哪些是圆周角,为什么?
B
A
甲O
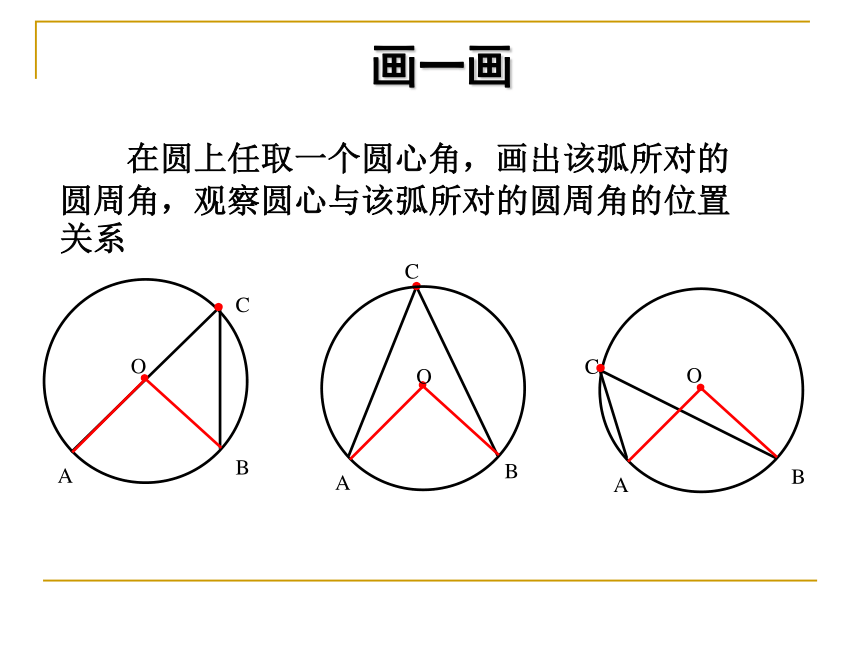
画一画
在圆上任取一个圆心角,画出该弧所对的圆周角,观察圆心与该弧所对的圆周角的位置关系
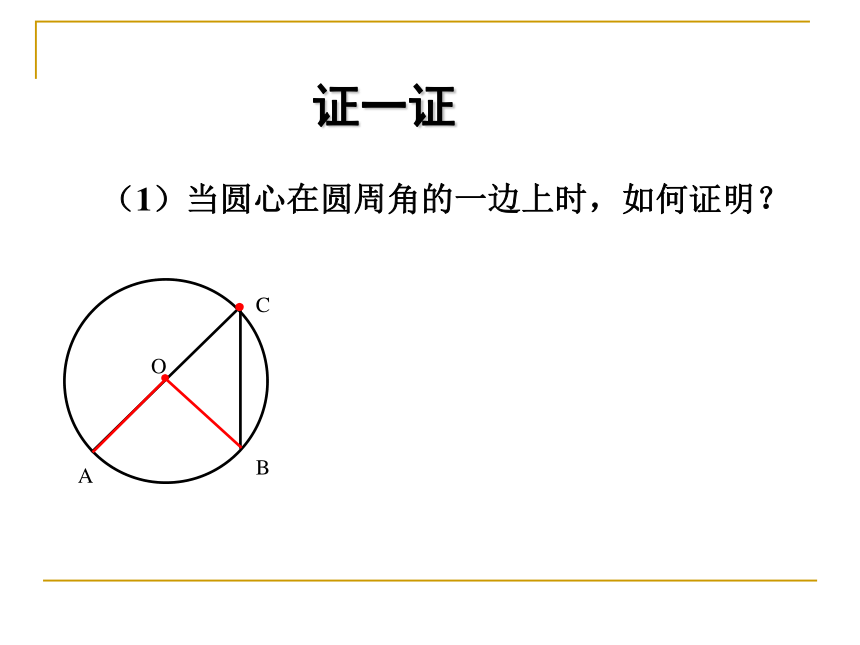
(1)当圆心在圆周角的一边上时,如何证明?
证一证
(2)当圆心在圆周角的内部时,如何证明?
证一证
D
(3)当圆心在圆周角的外部时,如何证明?
证一证
D
1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
练
习
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
辨析
1、圆周角的度数等于圆心角度数的一半
2、圆周角相等,则它们所对的弧也相等
4、同圆或等圆中,同弦或等弦所对的圆周角相等
3、等弧所对的圆周角相等
√
×
×
×
变式:弦AB分圆周为1:5两部分,则弦AB所对的圆周角的度数为?
?
例2:如图,OA⊥BC,
∠AOB=50°,试确定∠ADC的大小
例2、如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,判断△ABC的形状并证明你的结论。
(五)思考题
1、如图,矩形OABC内接于扇形MON,当CN=CO时,
∠NMB的度数是 _________ .
(五)思考题
如图,
MN是⊙O的直径,
MN=2,点
A在⊙O上,
∠AMN=30°
,B
为弧AN的中点,P
是直径
上
一动点,求
PA+PB的最小值
,
谈谈你这节课的收获?
感悟与收获
感谢指导!
圆周角(1)
观察思考:
在这个海洋馆里,人们可以通过其中的圆弧形玻璃窗观看窗内的海洋动物.
如图:同学甲站在圆心O的位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
思考?
如果同学丙、丁分别站在其他靠墙的位置D和E,
他们的视角(∠ADE和∠AEB)和同学乙的视
角相同吗?
观察:∠C
、∠D、∠E有什么共同的特征?
顶点在圆上
并且两边都和圆相交
圆周角
探索:判断下列各图中,哪些是圆周角,为什么?
B
A
甲O
画一画
在圆上任取一个圆心角,画出该弧所对的圆周角,观察圆心与该弧所对的圆周角的位置关系
(1)当圆心在圆周角的一边上时,如何证明?
证一证
(2)当圆心在圆周角的内部时,如何证明?
证一证
D
(3)当圆心在圆周角的外部时,如何证明?
证一证
D
1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
练
习
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
辨析
1、圆周角的度数等于圆心角度数的一半
2、圆周角相等,则它们所对的弧也相等
4、同圆或等圆中,同弦或等弦所对的圆周角相等
3、等弧所对的圆周角相等
√
×
×
×
变式:弦AB分圆周为1:5两部分,则弦AB所对的圆周角的度数为?
?
例2:如图,OA⊥BC,
∠AOB=50°,试确定∠ADC的大小
例2、如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,判断△ABC的形状并证明你的结论。
(五)思考题
1、如图,矩形OABC内接于扇形MON,当CN=CO时,
∠NMB的度数是 _________ .
(五)思考题
如图,
MN是⊙O的直径,
MN=2,点
A在⊙O上,
∠AMN=30°
,B
为弧AN的中点,P
是直径
上
一动点,求
PA+PB的最小值
,
谈谈你这节课的收获?
感悟与收获
感谢指导!
