北师大版九年级下册数学 2.4 二次函数的应用 课件(共14张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 2.4 二次函数的应用 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 14:42:48 | ||
图片预览




文档简介
(共14张PPT)
二次函数的应用
北师大版九年级数学下册
1.已知二次函数
,求其图像的顶点坐标。
2.已知二次函数图象的顶点坐标是(6
,2.6),且经过点(0,2),求其表达式
3.已知抛物线
过点(3,
)、(0,
4),求抛物线的表达式。
前置练习
1.顶点坐标的求法:配方法、公式法
、代入法。
2、抛物线与y轴交点:令x=0;
与x轴交点:令y=0。
(1)已知顶点坐标,设顶点式
3.二次函数关系式的求法:
(2)其他情况设一般式。
小结:
例1:这是王强在训练掷铅球时的高度y(m)与水平距离x(m)之间的函数图像,其关系式为
,则铅球达到的最大高度是_____米,此时离投掷点的水平距离是____米。铅球出手时的高度是_____米,此次掷铅球的成绩是____米。
4
3
10
M
N
如图,排球运动员站在点O处练习发球,将球从O点正上
方2
m的A处发出,把球看成点,球在水平距离运行6米达
到最大高度2.6米,球运行的高度记为y(m),水平距离
记为x(m),建立平面平面直角坐标系如图。
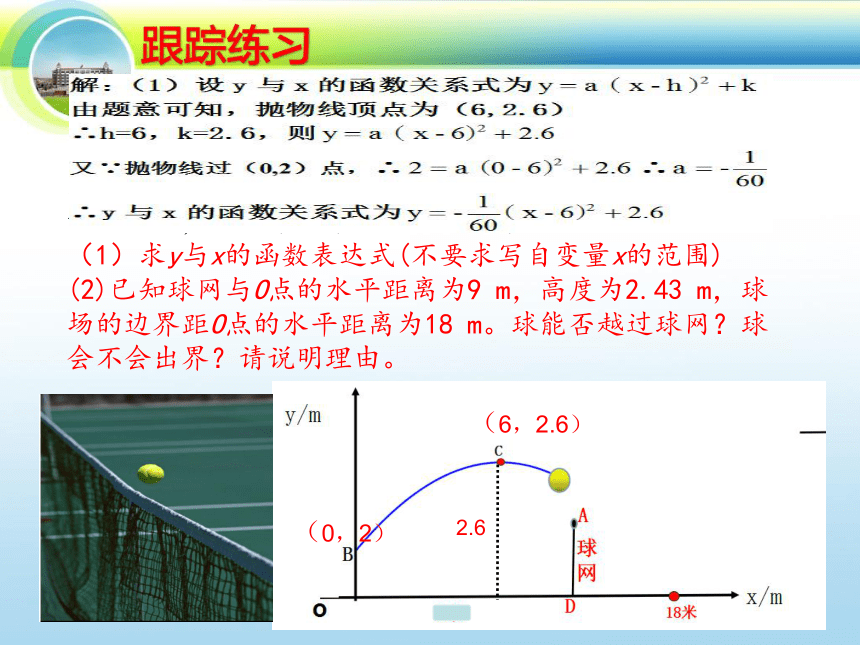
(1)求y与x的函数表达式(不要求写自变量x的范围)
(2)已知球网与O点的水平距离为9
m,高度为2.43
m,球
场的边界距O点的水平距离为18
m。球能否越过球网?球
会不会出界?请说明理由。
2.6
(6,2.6)
(0,2)
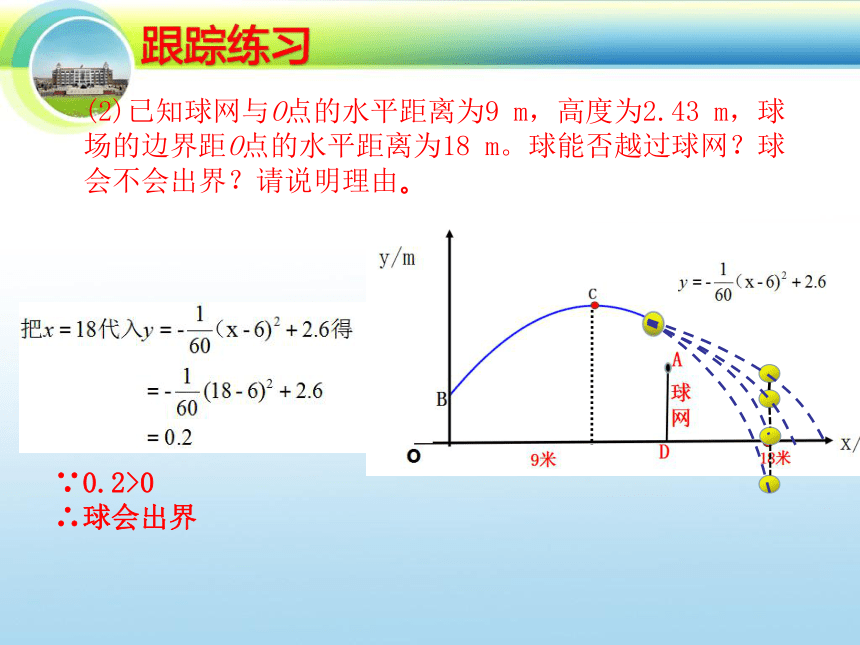
(2)已知球网与O点的水平距离为9
m,高度为2.43
m,球
场的边界距O点的水平距离为18
m。球能否越过球网?球
会不会出界?请说明理由。
∵0.2>0
∴球会出界
归纳提升
1、线段的长
点的坐标,求出表达式;
2、将点的一个坐标
表达式求另一个坐标;
3、将求出的坐标
实际问题的答案。
转化
转化
代入
关键:
线段的长与坐标的互相转化
抛物线型问题的解题思路:
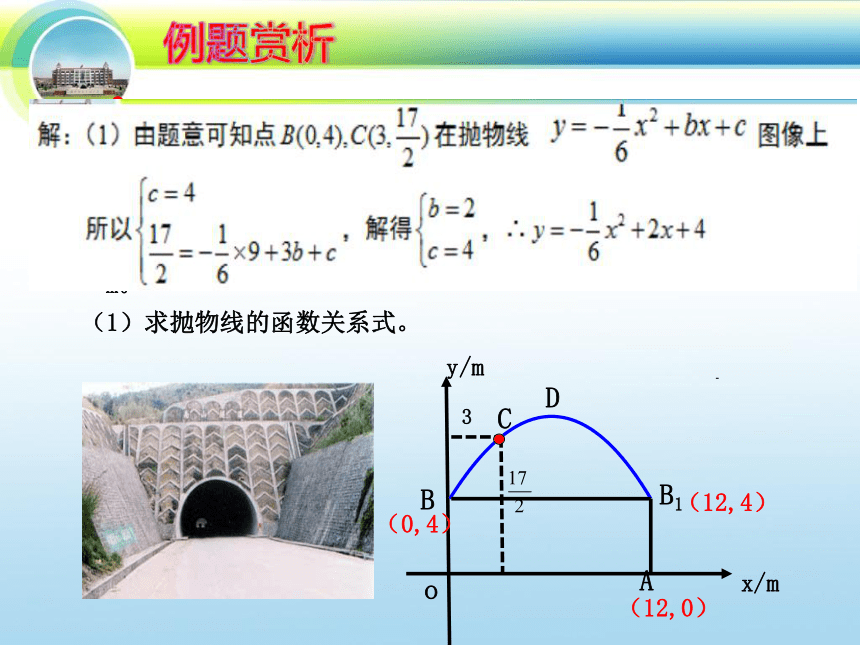
例2:青岛胶州湾隧道,是国内长度第一、世界排名第三的海底隧道。隧道的截面由抛物线和长方形构成,如图,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
m。?
o
D
A
C
B
B1
(0,4)
(12,4)
(12,0)
(1)求抛物线的函数关系式。?
y/m
x/m
3
2,
2
4
8
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设单向车道,那么这辆货车能否安全通过??
o
A
B
B1
y/m
x/m
?
6
C
D
一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过??
6
4m
2
10
4m
o
D
A
B
B1
y/m
x/m
o
D
A
B
B1
一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,且中间有2米的隔离带,那么这辆货车能否安全通过??
6
4m
1
4m
y/m
x/m
2
谈我所获
通过本节课的学习,你都有哪些感悟与收获?
我的收获是……
我的感悟是……
(1)建立二次函数模型。(求表达式)
(2)代入点的其中一个的坐标,求另一坐标。
(3)将坐标转化为问题答案
。
一、解决抛物线型问题的思路
三、数学思想:
数形结合
谈我所获
二、关键:
线段的长与坐标之间的互相转化
1、复习案剩余题目
作业
2、搜集、整理二次函数营销方面的典型例题。
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切。--克莱因.
谢谢
二次函数的应用
北师大版九年级数学下册
1.已知二次函数
,求其图像的顶点坐标。
2.已知二次函数图象的顶点坐标是(6
,2.6),且经过点(0,2),求其表达式
3.已知抛物线
过点(3,
)、(0,
4),求抛物线的表达式。
前置练习
1.顶点坐标的求法:配方法、公式法
、代入法。
2、抛物线与y轴交点:令x=0;
与x轴交点:令y=0。
(1)已知顶点坐标,设顶点式
3.二次函数关系式的求法:
(2)其他情况设一般式。
小结:
例1:这是王强在训练掷铅球时的高度y(m)与水平距离x(m)之间的函数图像,其关系式为
,则铅球达到的最大高度是_____米,此时离投掷点的水平距离是____米。铅球出手时的高度是_____米,此次掷铅球的成绩是____米。
4
3
10
M
N
如图,排球运动员站在点O处练习发球,将球从O点正上
方2
m的A处发出,把球看成点,球在水平距离运行6米达
到最大高度2.6米,球运行的高度记为y(m),水平距离
记为x(m),建立平面平面直角坐标系如图。
(1)求y与x的函数表达式(不要求写自变量x的范围)
(2)已知球网与O点的水平距离为9
m,高度为2.43
m,球
场的边界距O点的水平距离为18
m。球能否越过球网?球
会不会出界?请说明理由。
2.6
(6,2.6)
(0,2)
(2)已知球网与O点的水平距离为9
m,高度为2.43
m,球
场的边界距O点的水平距离为18
m。球能否越过球网?球
会不会出界?请说明理由。
∵0.2>0
∴球会出界
归纳提升
1、线段的长
点的坐标,求出表达式;
2、将点的一个坐标
表达式求另一个坐标;
3、将求出的坐标
实际问题的答案。
转化
转化
代入
关键:
线段的长与坐标的互相转化
抛物线型问题的解题思路:
例2:青岛胶州湾隧道,是国内长度第一、世界排名第三的海底隧道。隧道的截面由抛物线和长方形构成,如图,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
m。?
o
D
A
C
B
B1
(0,4)
(12,4)
(12,0)
(1)求抛物线的函数关系式。?
y/m
x/m
3
2,
2
4
8
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设单向车道,那么这辆货车能否安全通过??
o
A
B
B1
y/m
x/m
?
6
C
D
一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过??
6
4m
2
10
4m
o
D
A
B
B1
y/m
x/m
o
D
A
B
B1
一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,且中间有2米的隔离带,那么这辆货车能否安全通过??
6
4m
1
4m
y/m
x/m
2
谈我所获
通过本节课的学习,你都有哪些感悟与收获?
我的收获是……
我的感悟是……
(1)建立二次函数模型。(求表达式)
(2)代入点的其中一个的坐标,求另一坐标。
(3)将坐标转化为问题答案
。
一、解决抛物线型问题的思路
三、数学思想:
数形结合
谈我所获
二、关键:
线段的长与坐标之间的互相转化
1、复习案剩余题目
作业
2、搜集、整理二次函数营销方面的典型例题。
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切。--克莱因.
谢谢
