苏科版七年级下册数学课件: 7.5 三角形内角和定理的再思考(共17张PPT)
文档属性
| 名称 | 苏科版七年级下册数学课件: 7.5 三角形内角和定理的再思考(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
初中数学七年级下册(苏科版)
三角形内角和定理的再思考
三角形三个内角的和是多少度?
请你回顾三角形内角和定理是如何得出的?
复习回顾
三角形内角和定理:
三角形三个内角的和等于180
°
复习回顾
三角形内角和定理的推论:
1.三角形的一个外角等于与它不相邻的
两个内角的和;
2.三角形的一个外角大于任何一个和它
不相邻的内角.
动手操作
在直角△ABC中,∠A=
90o
折叠△ABC,使BA边与BC边重合,CA边与CB边重合,这两条折痕是△ABC的什么线?
动手操作
假设两条折痕的交点为O,你能否求出∠BOC的度数?
探索活动
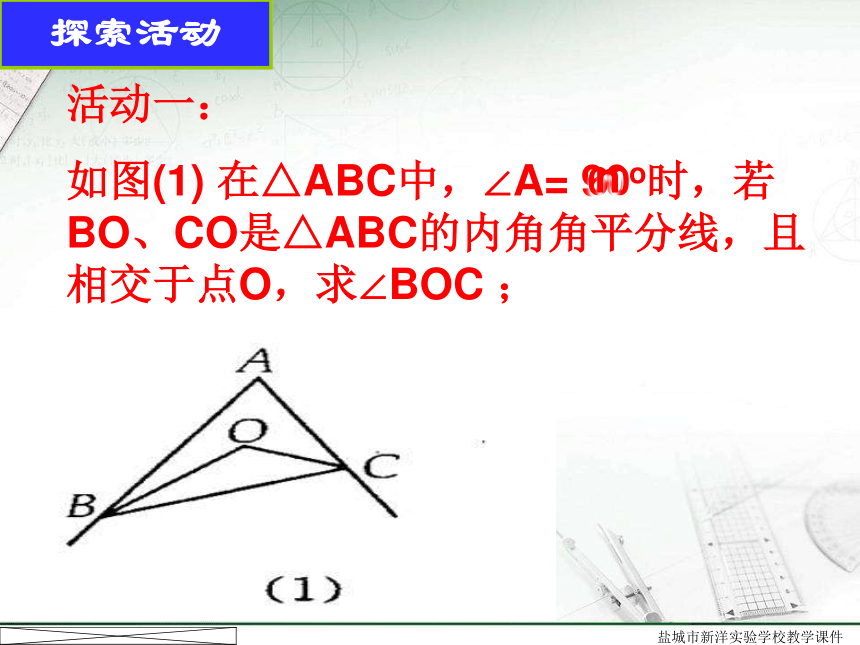
活动一:
如图(1)
在△ABC中,∠A=
90o时,若BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC
;
60
n
探索活动
活动二:
如图(2)
在△ABC中,∠A=
no时,若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
探索活动
活动三:
如图(3)
在△ABC中,∠A=
no时,若BO、CO是△ABC的一内角与一外角角平分线,且相交于点O,求∠BOC。
如图,在△ABC中,∠A=60o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平分∠EBC、
∠ECQ,则∠F=
。
知识应用
困难像弹簧,你强它就弱
如图,在⊿ABC中,∠A=60
o,BD、CD分别平分∠
ABC、
∠ACB,则∠D=
。
M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平分∠EBC、
∠ECQ,则∠F=
。
知识应用
牛刀小试
直线MN与直线PQ垂直相交于O,点A在直线PQ
上运动,点B在直线MN上运动。
如图,已AE、BE分别是∠
BAO和∠
ABO的角平分线,点A、B在运动的过程中,
∠
AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠
AEB的大小。
如图,在⊿ABC中,∠A=60o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,则∠E=
。
知识应用
如图,在⊿ABC中,∠A=
60
o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平∠EBC、
∠ECQ,则∠F=
。
知识应用
牛刀小试
直线MN与直线PQ垂直相交于O,点A在直线PQ
上运动,点B在直线MN上运动。
如图,已AE、BE分别是∠
BAO和∠
ABO的角平分线,点A、B在运动的过程中,
∠
AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠
AEB的大小。
不积跬步,无以至千里;
不积小流,无以成江海。
课后思考
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A'的位置时.聪明的同学,你能猜想出∠
A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A‘的位置时.聪明的同学,你能猜
想出∠
A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.
课后思考
小结
我感悟了:
1.三角形的两内角平分线(两个外角平分线或内外角平分线)所形成的角与第三个角之间特定关系
2.只要我们用心去观察,耐心地去发现,定会发现数学之美,生活之美。
初中数学七年级下册(苏科版)
三角形内角和定理的再思考
三角形三个内角的和是多少度?
请你回顾三角形内角和定理是如何得出的?
复习回顾
三角形内角和定理:
三角形三个内角的和等于180
°
复习回顾
三角形内角和定理的推论:
1.三角形的一个外角等于与它不相邻的
两个内角的和;
2.三角形的一个外角大于任何一个和它
不相邻的内角.
动手操作
在直角△ABC中,∠A=
90o
折叠△ABC,使BA边与BC边重合,CA边与CB边重合,这两条折痕是△ABC的什么线?
动手操作
假设两条折痕的交点为O,你能否求出∠BOC的度数?
探索活动
活动一:
如图(1)
在△ABC中,∠A=
90o时,若BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC
;
60
n
探索活动
活动二:
如图(2)
在△ABC中,∠A=
no时,若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
探索活动
活动三:
如图(3)
在△ABC中,∠A=
no时,若BO、CO是△ABC的一内角与一外角角平分线,且相交于点O,求∠BOC。
如图,在△ABC中,∠A=60o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平分∠EBC、
∠ECQ,则∠F=
。
知识应用
困难像弹簧,你强它就弱
如图,在⊿ABC中,∠A=60
o,BD、CD分别平分∠
ABC、
∠ACB,则∠D=
。
M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平分∠EBC、
∠ECQ,则∠F=
。
知识应用
牛刀小试
直线MN与直线PQ垂直相交于O,点A在直线PQ
上运动,点B在直线MN上运动。
如图,已AE、BE分别是∠
BAO和∠
ABO的角平分线,点A、B在运动的过程中,
∠
AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠
AEB的大小。
如图,在⊿ABC中,∠A=60o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,则∠E=
。
知识应用
如图,在⊿ABC中,∠A=
60
o,BD、CD分别平分∠
ABC、
∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、
∠BCN,BF、CF分别平∠EBC、
∠ECQ,则∠F=
。
知识应用
牛刀小试
直线MN与直线PQ垂直相交于O,点A在直线PQ
上运动,点B在直线MN上运动。
如图,已AE、BE分别是∠
BAO和∠
ABO的角平分线,点A、B在运动的过程中,
∠
AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠
AEB的大小。
不积跬步,无以至千里;
不积小流,无以成江海。
课后思考
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A'的位置时.聪明的同学,你能猜想出∠
A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A‘的位置时.聪明的同学,你能猜
想出∠
A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.
课后思考
小结
我感悟了:
1.三角形的两内角平分线(两个外角平分线或内外角平分线)所形成的角与第三个角之间特定关系
2.只要我们用心去观察,耐心地去发现,定会发现数学之美,生活之美。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
