苏科版八年级数学下册第9章 中心对称图形—— 平行四边形测试题含答案
文档属性
| 名称 | 苏科版八年级数学下册第9章 中心对称图形—— 平行四边形测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-30 13:59:42 | ||
图片预览

文档简介
第9章
中心对称图形——平行四边形测试题
一、选择题(每小题3分,共30分)
1.
已知□ABCD的周长为32,AB=4,则BC的长是(
)
A.
4
B.
12
C.
24
D.
28
2.如图1,在菱形ABCD中,∠BAD=120°,若△ABC的周长是15,则菱形ABCD的周长是(
)
A.25
B.
20
C.15
D.10
图1
图2
图3
3.
下列条件中,不能判定四边形ABCD是平行四边形的是(
)
A.
∠A=∠C,∠B=∠D
B.
AB∥CD,AB=CD
C.
AB∥CD,AD∥BC
D.
AB=CD,AD∥BC
4.
如图2,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.
若∠EFG=58°,则∠FEG的度数是(
)
A.
58°
B.
60°
C.
45°
D.
30°
5.
下列命题:①对角线相等的四边形是矩形;②三个角是直角的四边形是矩形;③有一个角是直角
的平行四边形是矩形.其中是真命题的有(
)
A.
3个
B.
2个
C.
1个
D.
0个
6.
如图3,将△ABC绕点C顺时针方向旋转40°得到△A′B′C,若AC⊥A′B′于点D,连接AA′,则∠AA′B′的度数为(
)
A.60°
B.50°
C.40°
D.20°
7.如图4,在正方形ABCD的外侧作等边三角形ADE,连接BE交AD于点F,则∠DFE的度数为(
)
A.
45°
B.
55°
C.
60°
D.
75°
图4
图5
图6
8.
如图5,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
则四边形ABCD的面积为(
)
A.
6
B.
12
C.
20
D.
24
9.
学习了正方形之后,小文给同桌小虎出了道题.下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.从中任选两个条件,使□ABCD成为正方形,其中错误的选法是(
)
A.
①②
B.
②③
C.
①③
D.
②④
10.
如图6,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第2018个三角形的周长为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共18分)
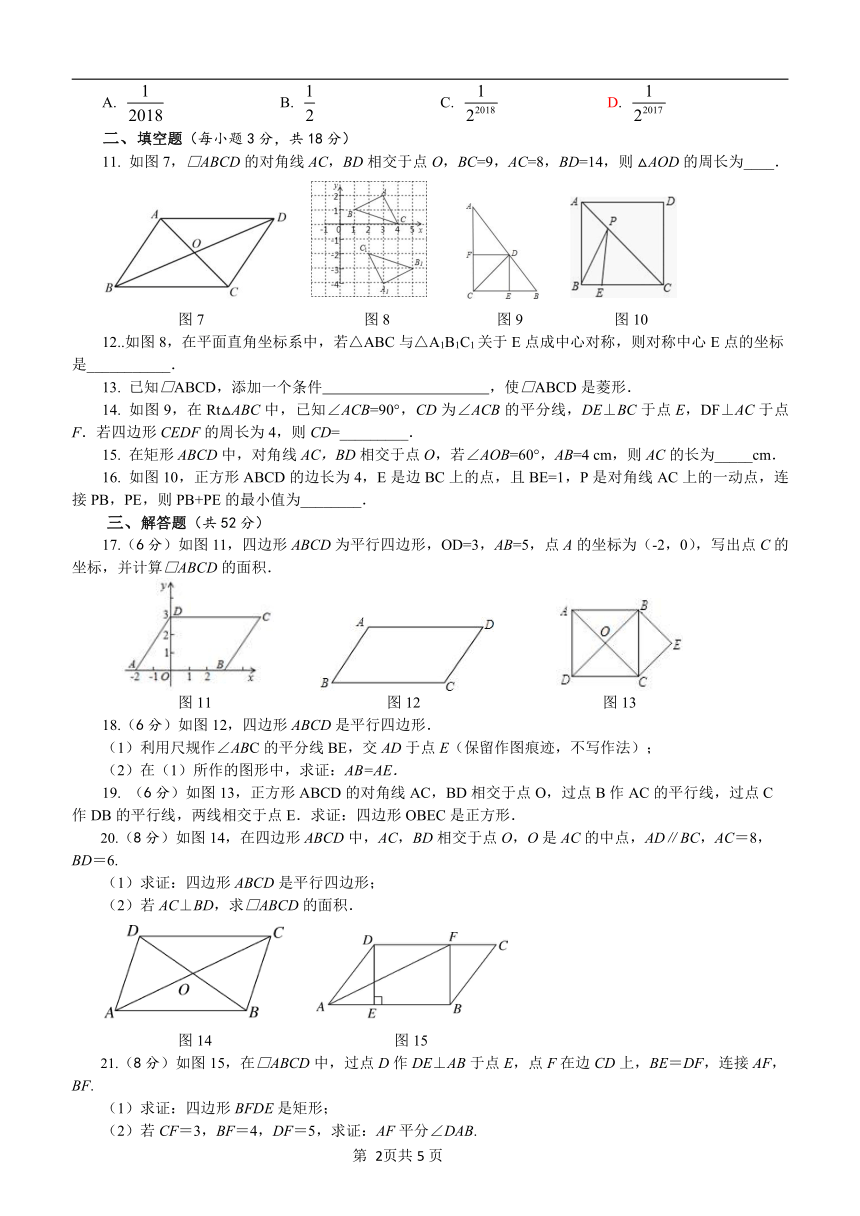
11.
如图7,□ABCD?的对角线?AC,BD?相交于点?O,BC=9,AC=8,BD=14,则?△AOD?的周长为____.
图7
图8
图9
图10
12..如图8,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是___________.
13.
已知□ABCD,添加一个条件
,使□ABCD是菱形.
14.
如图9,在Rt△ABC中,已知∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.若四边形CEDF的周长为4,则CD=_________.
15.
在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4
cm,则AC的长为_____cm.
16.
如图10,正方形ABCD的边长为4,E是边BC上的点,且BE=1,P是对角线AC上的一动点,连接PB,PE,则PB+PE的最小值为________.
三、解答题(共52分)
17.(6分)如图11,四边形ABCD为平行四边形,OD=3,AB=5,点A的坐标为(-2,0),写出点C的坐标,并计算□ABCD的面积.
图11
图12
图13
18.(6分)如图12,四边形ABCD是平行四边形.
(1)利用尺规作∠ABC的平分线BE,交AD于点E(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求证:AB=AE.
19.
(6分)如图13,正方形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线,过点C作DB的平行线,两线相交于点E.求证:四边形OBEC是正方形.
20.(8分)如图14,在四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
图14
图15
21.(8分)如图15,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,BE=DF,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
22.(9分)在课外活动中,我们要研究一种四边形——筝形的性质.
定义:两组邻边分别相等的四边形是筝形(如图16-①).
小聪根据学习平行四边形、菱形、矩形、正方形的经验,对筝形的性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)根据筝形的定义,写出一种你学过的满足筝形定义的四边形是________;
(2)通过观察、测量、折叠等操作活动,写出两条对筝形性质的猜想,并选取其中的一条猜想进行证明;
(3)如图16-②,在筝形ABCD中,AB=4,BC=2,∠ABC=120°,求筝形ABCD的面积.
图16
图17
23.(9分)如图17,在△ABC中,O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠ACD的平分线于点F,D为BC延长线上的点.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
附加题(20分,不计入总分)
24.
如图18-①,在矩形纸片ABCD中,AB=3
cm,AD=5
cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时(如图18-②),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
图18
参考答案
第9章
中心对称图形——平行四边形测试题
一、1.
B
2.
B
3.
D
4.
A
5.
B
6.D
7.
D
8.
D
9.
B
10.
D
二、11.
20
12.
(3,-1)
13.
答案不唯一,如AB=BC或AC⊥BD
14.
15.
8
16.
6
三、17.
解:由图知点B(3,0),D(0,3).因为CD=AB=5,所以点C的坐标为C(5,3).
□ABCD的面积=AB?OD=5×3=15.
18.(1)解:如图所示.
(2)证明:由(1),得∠ABE=∠CBE.
因为四边形ABCD是平行四边形,所以AD∥BC.
所以∠AEB=∠CBE.所以∠ABE=∠AEB.所以AB=AE.
19.
证明:因为BE∥OC,CE∥OB,所以四边形OBEC是平行四边形.
因为四边形ABCD是正方形,所以OC=OB,AC⊥BD.所以∠BOC=90°.所以四边形OBEC是矩形.
又因为OC=OB,所以四边形OBEC是正方形.
20.(1)证明:因为O是AC的中点,所以OA=OC.因为AD∥BC,所以∠ADO=∠CBO.
在△AOD和△COB中,∠ADO=∠CBO,∠AOD=∠COB,OA=OC,所以△AOD≌△COB.
所以OD=OB.所以四边形ABCD是平行四边形.
(2)解:因为四边形ABCD是平行四边形,AC⊥BD,所以四边形ABCD是菱形.
所以S菱形ABCD=AC·BD=×8×6=24.
21.
证明:(1)因为四边形ABCD是平行四边形,所以BE∥DF.又因为BE=DF,所以四边形BFDE是平行四边形.因为DE⊥AB,所以∠DEB=90°.所以四边形BFDE是矩形.
(2)因为四边形ABCD是平行四边形,所以AD=BC,AB∥DC.所以∠DFA=∠FAB.
由(1)可知四边形BFDE是矩形,所以∠BFD=90°.所以∠BFC=90°.
在Rt△BCF中,由勾股定理,得BC=5,所以AD=BC=5.因为DF=5,所以AD=DF.
所以∠DAF=∠DFA.所以∠DAF=∠FAB,即AF平分∠DAB.
22.
解:(1)菱形(或正方形)
(2)它是一个轴对称图形;一组对角相等;一条对角线所在的直线垂直平分另一条对角线(写出其中的两条即可).选取“一组对角相等”进行证明.证明如下:
已知:四边形ABCD是筝形.求证:∠B=∠D.
证明:连接AC.因为四边形ABCD是筝形,所以AB=AD,CB=CD.
又因为AC=AC,所以△ABC≌△ADC.所以∠B=∠D.
(3)连接AC,易知S筝形ABCD=2S△ABC.过点C作CE⊥AB交AB的延长线于点E,则∠E=90°.
因为∠ABC=120°,所以∠EBC=60°.所以∠ECB=30°.
又因为BC=2,所以BE=1.所以CE==.
所以S筝形ABCD=2S△ABC=2×AB·CE=2××4×=4.
23.
证明:(1)因为MN交∠BCA的平分线于点E,交∠ACD的平分线于点F,所以∠ECO=∠BCE,∠DCF=∠OCF.
又因为直线MN∥BC,所以∠BCE=∠CEO,∠DCF=∠CFO.
所以∠ECO=∠CEO,∠CFO=∠OCF.所以EO=CO,CO=FO.所以
EO=FO.
(2)当点O运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=OC.又因为EO=FO,所以四边形AECF是平行四边形.
由(1)知CO
=EF,又CO
=AC,所以EF=AC.所以四边形AECF是矩形.
24.(1)证明:由折叠可得BP=EP,∠BPF=∠EPF.
又因为PF=PF,所以△PBF≌△PEF.所以BF=EF.
因为EF∥AB,所以∠BPF=∠EFP.所以∠EPF=∠EFP.所以EP=EF.
所以BP=BF=EF=EP.所以四边形BFEP为菱形.
(2)解:①因为四边形ABCD是矩形,所以BC=AD=5
cm,CD=AB=3
cm,∠A=∠D=90°.
由折叠可得BP=EP,CE=BC=5
cm.
在Rt△CDE中,由勾股定理,得DE=4
cm.所以AE=AD-DE=5-4=1(cm).
设BP=EP=x
cm,则AP=(3-x)cm.
在Rt△APE中,由勾股定理,得EP2=AE2+AP2,即x2=12+(3-x)2,解得x=.
所以菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1
cm.
当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3
cm.
3-1=2(cm),所以点E在边AD上移动的最大距离为2
cm.
第
1页共5页
中心对称图形——平行四边形测试题
一、选择题(每小题3分,共30分)
1.
已知□ABCD的周长为32,AB=4,则BC的长是(
)
A.
4
B.
12
C.
24
D.
28
2.如图1,在菱形ABCD中,∠BAD=120°,若△ABC的周长是15,则菱形ABCD的周长是(
)
A.25
B.
20
C.15
D.10
图1
图2
图3
3.
下列条件中,不能判定四边形ABCD是平行四边形的是(
)
A.
∠A=∠C,∠B=∠D
B.
AB∥CD,AB=CD
C.
AB∥CD,AD∥BC
D.
AB=CD,AD∥BC
4.
如图2,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.
若∠EFG=58°,则∠FEG的度数是(
)
A.
58°
B.
60°
C.
45°
D.
30°
5.
下列命题:①对角线相等的四边形是矩形;②三个角是直角的四边形是矩形;③有一个角是直角
的平行四边形是矩形.其中是真命题的有(
)
A.
3个
B.
2个
C.
1个
D.
0个
6.
如图3,将△ABC绕点C顺时针方向旋转40°得到△A′B′C,若AC⊥A′B′于点D,连接AA′,则∠AA′B′的度数为(
)
A.60°
B.50°
C.40°
D.20°
7.如图4,在正方形ABCD的外侧作等边三角形ADE,连接BE交AD于点F,则∠DFE的度数为(
)
A.
45°
B.
55°
C.
60°
D.
75°
图4
图5
图6
8.
如图5,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
则四边形ABCD的面积为(
)
A.
6
B.
12
C.
20
D.
24
9.
学习了正方形之后,小文给同桌小虎出了道题.下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.从中任选两个条件,使□ABCD成为正方形,其中错误的选法是(
)
A.
①②
B.
②③
C.
①③
D.
②④
10.
如图6,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,则第2018个三角形的周长为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共18分)
11.
如图7,□ABCD?的对角线?AC,BD?相交于点?O,BC=9,AC=8,BD=14,则?△AOD?的周长为____.
图7
图8
图9
图10
12..如图8,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是___________.
13.
已知□ABCD,添加一个条件
,使□ABCD是菱形.
14.
如图9,在Rt△ABC中,已知∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.若四边形CEDF的周长为4,则CD=_________.
15.
在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4
cm,则AC的长为_____cm.
16.
如图10,正方形ABCD的边长为4,E是边BC上的点,且BE=1,P是对角线AC上的一动点,连接PB,PE,则PB+PE的最小值为________.
三、解答题(共52分)
17.(6分)如图11,四边形ABCD为平行四边形,OD=3,AB=5,点A的坐标为(-2,0),写出点C的坐标,并计算□ABCD的面积.
图11
图12
图13
18.(6分)如图12,四边形ABCD是平行四边形.
(1)利用尺规作∠ABC的平分线BE,交AD于点E(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求证:AB=AE.
19.
(6分)如图13,正方形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线,过点C作DB的平行线,两线相交于点E.求证:四边形OBEC是正方形.
20.(8分)如图14,在四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
图14
图15
21.(8分)如图15,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,BE=DF,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
22.(9分)在课外活动中,我们要研究一种四边形——筝形的性质.
定义:两组邻边分别相等的四边形是筝形(如图16-①).
小聪根据学习平行四边形、菱形、矩形、正方形的经验,对筝形的性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)根据筝形的定义,写出一种你学过的满足筝形定义的四边形是________;
(2)通过观察、测量、折叠等操作活动,写出两条对筝形性质的猜想,并选取其中的一条猜想进行证明;
(3)如图16-②,在筝形ABCD中,AB=4,BC=2,∠ABC=120°,求筝形ABCD的面积.
图16
图17
23.(9分)如图17,在△ABC中,O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠ACD的平分线于点F,D为BC延长线上的点.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
附加题(20分,不计入总分)
24.
如图18-①,在矩形纸片ABCD中,AB=3
cm,AD=5
cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时(如图18-②),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
图18
参考答案
第9章
中心对称图形——平行四边形测试题
一、1.
B
2.
B
3.
D
4.
A
5.
B
6.D
7.
D
8.
D
9.
B
10.
D
二、11.
20
12.
(3,-1)
13.
答案不唯一,如AB=BC或AC⊥BD
14.
15.
8
16.
6
三、17.
解:由图知点B(3,0),D(0,3).因为CD=AB=5,所以点C的坐标为C(5,3).
□ABCD的面积=AB?OD=5×3=15.
18.(1)解:如图所示.
(2)证明:由(1),得∠ABE=∠CBE.
因为四边形ABCD是平行四边形,所以AD∥BC.
所以∠AEB=∠CBE.所以∠ABE=∠AEB.所以AB=AE.
19.
证明:因为BE∥OC,CE∥OB,所以四边形OBEC是平行四边形.
因为四边形ABCD是正方形,所以OC=OB,AC⊥BD.所以∠BOC=90°.所以四边形OBEC是矩形.
又因为OC=OB,所以四边形OBEC是正方形.
20.(1)证明:因为O是AC的中点,所以OA=OC.因为AD∥BC,所以∠ADO=∠CBO.
在△AOD和△COB中,∠ADO=∠CBO,∠AOD=∠COB,OA=OC,所以△AOD≌△COB.
所以OD=OB.所以四边形ABCD是平行四边形.
(2)解:因为四边形ABCD是平行四边形,AC⊥BD,所以四边形ABCD是菱形.
所以S菱形ABCD=AC·BD=×8×6=24.
21.
证明:(1)因为四边形ABCD是平行四边形,所以BE∥DF.又因为BE=DF,所以四边形BFDE是平行四边形.因为DE⊥AB,所以∠DEB=90°.所以四边形BFDE是矩形.
(2)因为四边形ABCD是平行四边形,所以AD=BC,AB∥DC.所以∠DFA=∠FAB.
由(1)可知四边形BFDE是矩形,所以∠BFD=90°.所以∠BFC=90°.
在Rt△BCF中,由勾股定理,得BC=5,所以AD=BC=5.因为DF=5,所以AD=DF.
所以∠DAF=∠DFA.所以∠DAF=∠FAB,即AF平分∠DAB.
22.
解:(1)菱形(或正方形)
(2)它是一个轴对称图形;一组对角相等;一条对角线所在的直线垂直平分另一条对角线(写出其中的两条即可).选取“一组对角相等”进行证明.证明如下:
已知:四边形ABCD是筝形.求证:∠B=∠D.
证明:连接AC.因为四边形ABCD是筝形,所以AB=AD,CB=CD.
又因为AC=AC,所以△ABC≌△ADC.所以∠B=∠D.
(3)连接AC,易知S筝形ABCD=2S△ABC.过点C作CE⊥AB交AB的延长线于点E,则∠E=90°.
因为∠ABC=120°,所以∠EBC=60°.所以∠ECB=30°.
又因为BC=2,所以BE=1.所以CE==.
所以S筝形ABCD=2S△ABC=2×AB·CE=2××4×=4.
23.
证明:(1)因为MN交∠BCA的平分线于点E,交∠ACD的平分线于点F,所以∠ECO=∠BCE,∠DCF=∠OCF.
又因为直线MN∥BC,所以∠BCE=∠CEO,∠DCF=∠CFO.
所以∠ECO=∠CEO,∠CFO=∠OCF.所以EO=CO,CO=FO.所以
EO=FO.
(2)当点O运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=OC.又因为EO=FO,所以四边形AECF是平行四边形.
由(1)知CO
=EF,又CO
=AC,所以EF=AC.所以四边形AECF是矩形.
24.(1)证明:由折叠可得BP=EP,∠BPF=∠EPF.
又因为PF=PF,所以△PBF≌△PEF.所以BF=EF.
因为EF∥AB,所以∠BPF=∠EFP.所以∠EPF=∠EFP.所以EP=EF.
所以BP=BF=EF=EP.所以四边形BFEP为菱形.
(2)解:①因为四边形ABCD是矩形,所以BC=AD=5
cm,CD=AB=3
cm,∠A=∠D=90°.
由折叠可得BP=EP,CE=BC=5
cm.
在Rt△CDE中,由勾股定理,得DE=4
cm.所以AE=AD-DE=5-4=1(cm).
设BP=EP=x
cm,则AP=(3-x)cm.
在Rt△APE中,由勾股定理,得EP2=AE2+AP2,即x2=12+(3-x)2,解得x=.
所以菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1
cm.
当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3
cm.
3-1=2(cm),所以点E在边AD上移动的最大距离为2
cm.
第
1页共5页
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
