沪科版九年级数学上册 21.5 反比例函数( 第2课时共19张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 21.5 反比例函数( 第2课时共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 495.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-01 13:57:57 | ||
图片预览



文档简介
(共19张PPT)
21.5.2
反比例函数(二)
x
k
y
=
1、反比例函数
(k是常数,k≠0)的自变量x
的取值范围有什么限制?
自变量x的取值范围是不等于0的一切实数,函
数y的值也不等于0。
k叫做比例系数,k≠0。
2、有时反比例函数也可写成xy=k(k≠0)或y=kx-1(k≠0)
x
k
y
=
(k≠0)
xy=k(k≠0)
y=kx-1(k≠0)
知识回顾
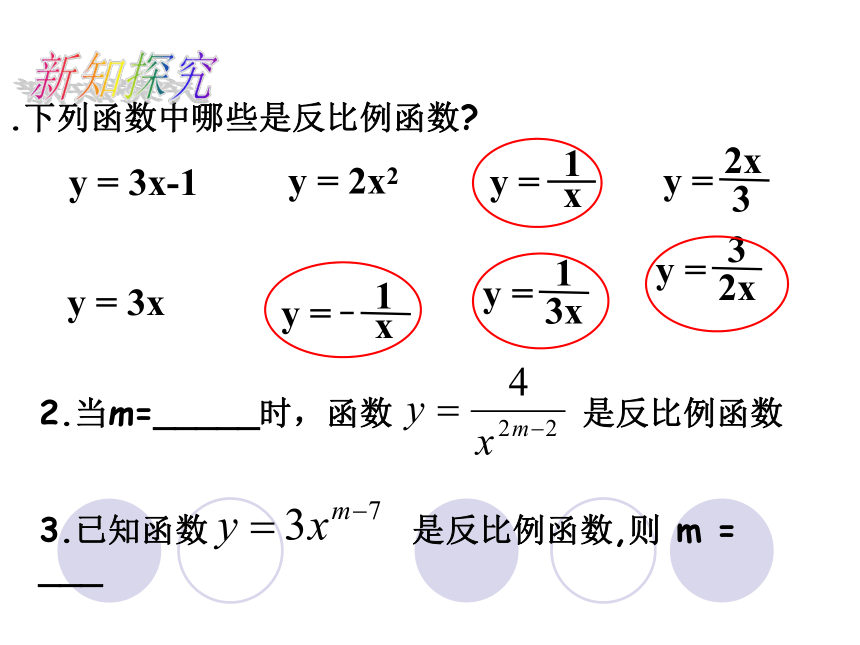
.下列函数中哪些是反比例函数?
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
x
1
2.当m=_____时,函数
是反比例函数
3.已知函数
是反比例函数,则
m
=
___
新知探究
变:若y与 x-2成反比例,又怎么设?
解:设
∵当
x=3时y=4,
∴
=4,所以k=
36
,
当x=
时,
y=
36÷(
)2=1296
x2
y
k
=
9
k
6
1
6
1
2、已知y
与
x2
成反比例,
并且当
x
=
3时y
=
4,求
x
=
时
y的值
6
1
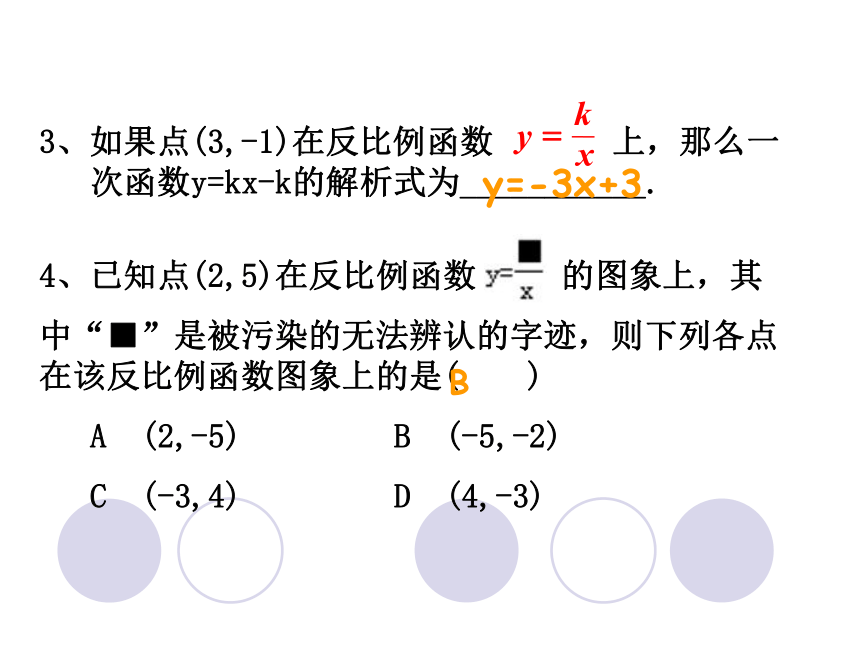
3、如果点(3,-1)在反比例函数
上,那么一
次函数y=kx-k的解析式为___________.
x
k
y
=
4、已知点(2,5)在反比例函数
的图象上,其
中“■”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是(
)
A
(2,-5)
B
(-5,-2)
C
(-3,4)
D
(4,-3)
y=-3x+3
B
x
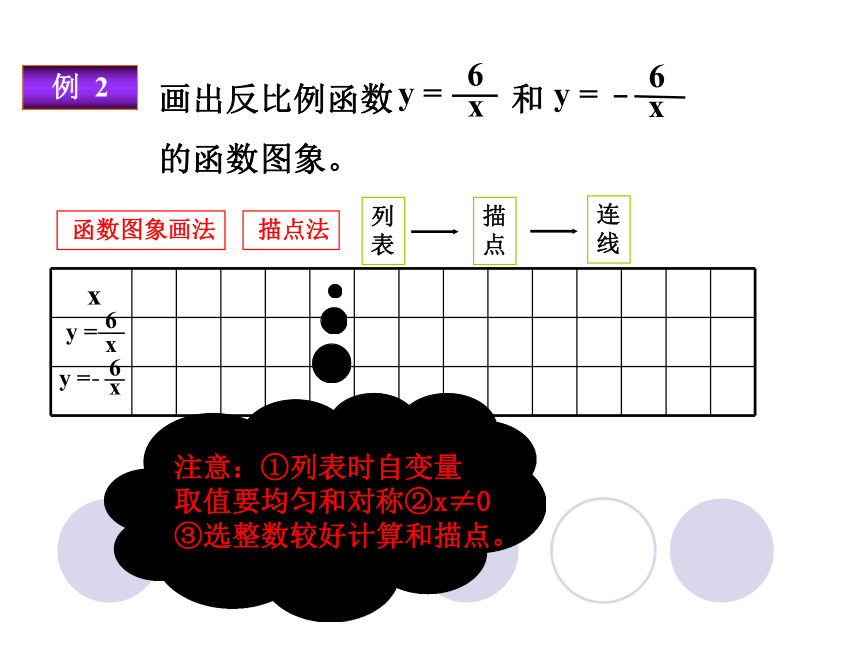
画出反比例函数
和
的函数图象。
y
=
x
6
y
=
x
6
函数图象画法
列
表
描
点
连
线
y
=
x
6
y
=
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
例
2
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y
=
x
6
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y
=
x
6
y
=
x
6
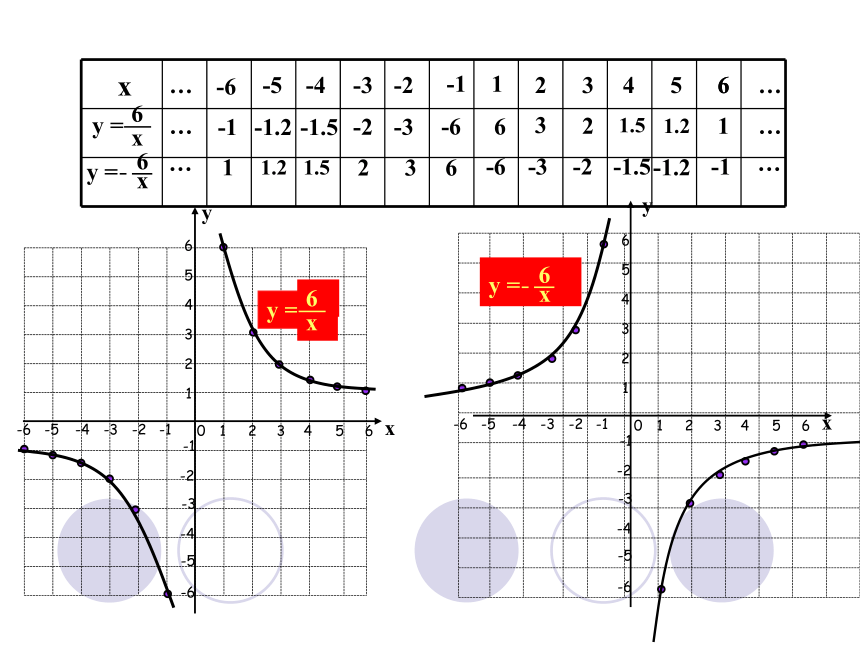
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大。
y
=
x
6
x
y
0
y
x
y
x
6
y
=
0
知识梳理
函数
正比例函数
反比例函数
解析式
图象
自变量取值范围
图象的位置
性质
当k>0时,y随x的增大而减小
当k<0时,y随x的增大而增大
正比例函数与反比例函数的对比
y=kx(k≠0)
全体实数
x≠0的一切实数
当k>0时,在一、三象限;
当k<0时,在二、四象限。
当k>0时,在一、三象限;
当k<0时,在二、四象限
当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
D
先假设某个函数图象已经画好,再确定另外的是否符合条件.
6、如图,函数
和y=-kx+1(k≠0)在同一坐标系
内的图象大致是(
)
A
B
C
D
y3<
y1<
y2
2、函数
的图象上有三点
(-3,y1),
(-1,y2),
(2,y3),则函数值y1、y2、y3的
大小关系是_______________;
3.已知y
与
x
成反比例,
并且当
x
=
2
时y
=
5,求
x
与
y
的函数关系式。
x
10
y
=
4.根据图形写出函数的解析式。
y
x
y
0
(-3,1)
y
=
x
3
如图:A、B是双曲线y=
上的
任意两点
。
过A、B两点分别作
x轴和y轴的垂线,试确定图中两
个三角形的面积各是多少?
5
x
x
y
o
A
y=
5
x
B
答:面积都是
。
5
2
想一想
练习:
1.下列函数中,其图象位于第一、三象限的有
__________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数
的图象上,比较y1、
y2
、y3的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x1,
x3=3>0,
∴点A(-2,y1),点B(-1,y2)在第三象限点C(3,y3)在第一象限。
∴y3>0,
y2
即y2
<
y1
<
0<
y3
(1)(2)(3)
(4)
你能解答第(2)小题了吗?
例:表示下面四个关系式的图像有
图像与性质
从函数的解析式、图象中获取信息
的能力是学好数学必需具有的
基本素质.
1.反比例函数y=k/x(k≠0)的图象是一个怎样的图象?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线
2.反比例函数的图象的位置与k有怎样关系?
知识梳理
3
反比例函数的图象可能与x轴相交吗?
可能与y轴相交吗?为什么?
不能与x轴、y轴相交。
因为x≠0,所以不与y轴相交;因为y
≠0,所以不与x轴相交。
结论:图像的两个分支无限接近x轴和y轴,但永远不会与X轴、y轴相交。
4、
将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?
能重合,双曲线是中心对称图形,
对称中心是原点。
能重合,双曲线是轴对称图形,有两条对称轴,是直线y=x和直线y=-x
5、
将反比例函数的图象沿着直线y=x或直线y=-x折叠后,两部分图象能重合吗?
2.你能再回顾一下反比例
函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时,
双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与
坐标轴相交
双曲线既是轴对称图形又是中心对称图形.
任意一组变量的乘积是一个定值,即xy=k
形
状
位
置
增减性
变化趋势
对称性
由定义求面积
共有6个
反比例函数的图象是轴对称图形.直线y=x和y=-x都是它的对称轴;
反比例函数
与
的图象关于x轴对称,也关于y轴对称。
惜时专心苦读是做学问的一个好方法。
21.5.2
反比例函数(二)
x
k
y
=
1、反比例函数
(k是常数,k≠0)的自变量x
的取值范围有什么限制?
自变量x的取值范围是不等于0的一切实数,函
数y的值也不等于0。
k叫做比例系数,k≠0。
2、有时反比例函数也可写成xy=k(k≠0)或y=kx-1(k≠0)
x
k
y
=
(k≠0)
xy=k(k≠0)
y=kx-1(k≠0)
知识回顾
.下列函数中哪些是反比例函数?
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
3
2x
y
=
1
3x
y
=
x
1
2.当m=_____时,函数
是反比例函数
3.已知函数
是反比例函数,则
m
=
___
新知探究
变:若y与 x-2成反比例,又怎么设?
解:设
∵当
x=3时y=4,
∴
=4,所以k=
36
,
当x=
时,
y=
36÷(
)2=1296
x2
y
k
=
9
k
6
1
6
1
2、已知y
与
x2
成反比例,
并且当
x
=
3时y
=
4,求
x
=
时
y的值
6
1
3、如果点(3,-1)在反比例函数
上,那么一
次函数y=kx-k的解析式为___________.
x
k
y
=
4、已知点(2,5)在反比例函数
的图象上,其
中“■”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是(
)
A
(2,-5)
B
(-5,-2)
C
(-3,4)
D
(4,-3)
y=-3x+3
B
x
画出反比例函数
和
的函数图象。
y
=
x
6
y
=
x
6
函数图象画法
列
表
描
点
连
线
y
=
x
6
y
=
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
例
2
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y
=
x
6
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y
=
x
6
y
=
x
6
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大。
y
=
x
6
x
y
0
y
x
y
x
6
y
=
0
知识梳理
函数
正比例函数
反比例函数
解析式
图象
自变量取值范围
图象的位置
性质
当k>0时,y随x的增大而减小
当k<0时,y随x的增大而增大
正比例函数与反比例函数的对比
y=kx(k≠0)
全体实数
x≠0的一切实数
当k>0时,在一、三象限;
当k<0时,在二、四象限。
当k>0时,在一、三象限;
当k<0时,在二、四象限
当k>0时,y随x的增大而增大
当k<0时,y随x的增大而减小
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
D
先假设某个函数图象已经画好,再确定另外的是否符合条件.
6、如图,函数
和y=-kx+1(k≠0)在同一坐标系
内的图象大致是(
)
A
B
C
D
y3<
y1<
y2
2、函数
的图象上有三点
(-3,y1),
(-1,y2),
(2,y3),则函数值y1、y2、y3的
大小关系是_______________;
3.已知y
与
x
成反比例,
并且当
x
=
2
时y
=
5,求
x
与
y
的函数关系式。
x
10
y
=
4.根据图形写出函数的解析式。
y
x
y
0
(-3,1)
y
=
x
3
如图:A、B是双曲线y=
上的
任意两点
。
过A、B两点分别作
x轴和y轴的垂线,试确定图中两
个三角形的面积各是多少?
5
x
x
y
o
A
y=
5
x
B
答:面积都是
。
5
2
想一想
练习:
1.下列函数中,其图象位于第一、三象限的有
__________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数
的图象上,比较y1、
y2
、y3的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x1
x3=3>0,
∴点A(-2,y1),点B(-1,y2)在第三象限点C(3,y3)在第一象限。
∴y3>0,
y2
<
y1
<
0<
y3
(1)(2)(3)
(4)
你能解答第(2)小题了吗?
例:表示下面四个关系式的图像有
图像与性质
从函数的解析式、图象中获取信息
的能力是学好数学必需具有的
基本素质.
1.反比例函数y=k/x(k≠0)的图象是一个怎样的图象?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线
2.反比例函数的图象的位置与k有怎样关系?
知识梳理
3
反比例函数的图象可能与x轴相交吗?
可能与y轴相交吗?为什么?
不能与x轴、y轴相交。
因为x≠0,所以不与y轴相交;因为y
≠0,所以不与x轴相交。
结论:图像的两个分支无限接近x轴和y轴,但永远不会与X轴、y轴相交。
4、
将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?
能重合,双曲线是中心对称图形,
对称中心是原点。
能重合,双曲线是轴对称图形,有两条对称轴,是直线y=x和直线y=-x
5、
将反比例函数的图象沿着直线y=x或直线y=-x折叠后,两部分图象能重合吗?
2.你能再回顾一下反比例
函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时,
双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与
坐标轴相交
双曲线既是轴对称图形又是中心对称图形.
任意一组变量的乘积是一个定值,即xy=k
形
状
位
置
增减性
变化趋势
对称性
由定义求面积
共有6个
反比例函数的图象是轴对称图形.直线y=x和y=-x都是它的对称轴;
反比例函数
与
的图象关于x轴对称,也关于y轴对称。
惜时专心苦读是做学问的一个好方法。
