3.1.3《频率与概率》课件(新人教B版必修三)
文档属性
| 名称 | 3.1.3《频率与概率》课件(新人教B版必修三) |  | |
| 格式 | rar | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-25 17:15:45 | ||
图片预览






文档简介
(共17张PPT)
3.1.3 频率与概率
事件(1)、(4)、(6)是必然事件;
事件(2)、(9)、(10)是不可能事件;
事件(3)、(5)、(7)、(8)是随机事件.
指出下列事件是必然事件,不可能事件,还是随机事件:
(1)“抛一石块,下落”.
(2)“在标准大气压下且温度低于0℃时,冰融化”;
(3)“某人射击一次,中靶”;
(4)“如果a,b都是实数,则a+b=a+b;”;
(5)“将一枚硬币抛掷4次出现两次正面和两次反面”;
(6)“导体通电后,发热”;
(7)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(8)“某电话机在1分钟内收到2次呼叫”;
(9)“没有水份,种子能发芽”;
(10)“在常温下,焊锡熔化”.
问:
随机事件发生或者不发生是
不是没有任何规律呢?
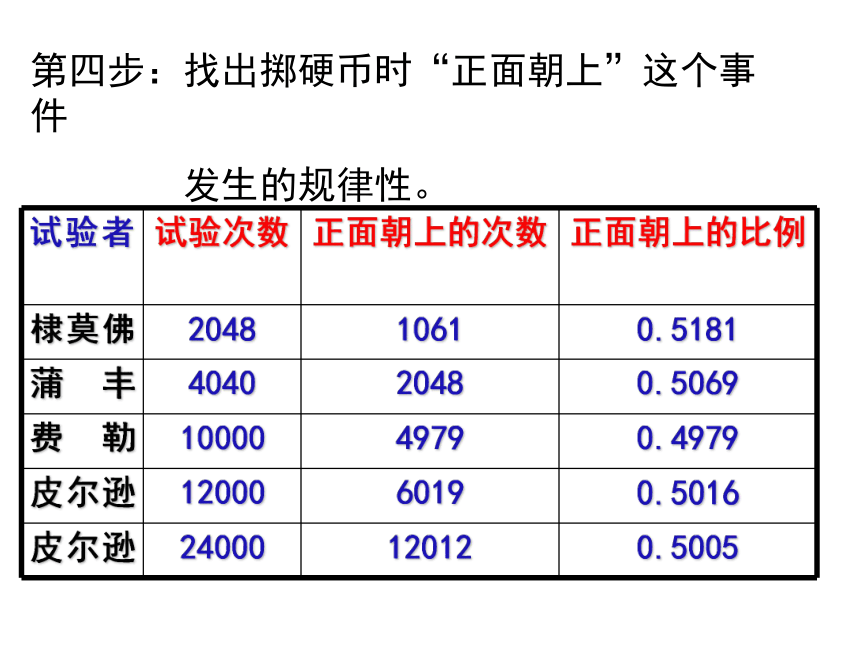
第四步:找出掷硬币时“正面朝上”这个事件
发生的规律性。
试验者 试验次数
正面朝上的次数
正面朝上的比例
棣莫佛 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
频数:在相同的条件S下重复n次试验,观察
某一事件A是否出现,称n次试验中事 件A出现的次数 nA 为事件A出现的频数。
频率:事件A出现的比例 为事
件A出现的频率。
(三)频数与频率
试验者 试验次数
正面朝上的频数
正面朝上的频率
棣莫佛 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
(四)随机事件A的概率
对于给定的随机事件A,如 果随着试验次数的增加,事件A发生的频率fn(A) 稳定在某个常数附近,把这个常数记作P(A),称为事件A的概率,简称为A 的概率。
例如:P(正面朝上)=
0.5
P(反面朝上)=
0.5
不可能事件的概率为
必然事件的概率为
0
1
研究随机现象,不仅关心试验中会出现哪些事件,更重要的是想知道事件出现的可能性大小,也就是事件的概率.
概率是随机事件
发生可能性大小
的度量
事件发生的可能性
越大,概率就
越大!
思考:随机事件A在重复试验中出现的
频率 是不是不变的?随机事件A的概
率是不是不变的?它们之间有什么区别与
联系?
(1)大量重复进行同一试验时,随机事件发生与否呈现出规律性:频率总在P(A)附近摆动,当试验次数越多时,摆动幅度越小。
(2)0≤P(A)≤1,不可能事件的概率为0,必然事件的概率为1,随机事件的概率大于0而小于1。
(3)在实际问题中,通常随机事件的概率未知,常用频率作为它的估计值。
例2 某射手在同一条件下进行射击,结果如下表所示:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是什么?
分析:事件A出现的频数nA与试验次数n的比值即为事件A的频率,当事件A发生的频率fn(A)稳定在某个常数上时,这个常数即为事件A的概率。
解:(1)表中依次填入的数据为:0.80,0.95,0.88,0.92,0.89,0.91.
(2)由于频率稳定在常数0.89,所以这个射手击一次,击中靶心的概率约是0.89。
概率实际上是频率的科学抽象,
求某事件的概率可以通过求该事件
的频率而得之
2.某人进行打靶练习,共射击10次,其中有2次中10环,有3次环中9环,有4次中8环,有1次未中靶,试计算此人中靶的频率,假设此人射击1次,试问中靶的频率约为多大?中10环的概率约为多大?
1.一个地区从某年起几年之内的新生儿数及其中男婴数如下:
时间范围 1年内 2年内 3年内 4年内
新生婴儿数 5544 9607 13520 17190
男婴数 2883 4970 6994 8892
男婴出生的频率
(1)填写表中男婴出生的频率(结果保留到小数点后第3位);
(2)这一地区男婴出生的概率约是多少?
练习:
自我评价与课堂练习:
1.将一枚硬币向上抛掷10次,其中正面向上恰有5次是( )
A.必然事件 B.随机事件
C.不可能事件 D.无法确定
2.下列说法正确的是( )
A.任一事件的概率总在(0.1)内
B.不可能事件的概率不一定为0
C.必然事件的概率一定为1
D.以上均不对
每批粒数 2 5 10 70 130 700 1500 2000 3000
发芽的粒数 2 4 9 60 116 282 639 1339 2715
发芽的频率
(1)完成上面表格:
(2)该油菜子发芽的概率约是多少?
4.生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了。”学了概率后,你能给出解释吗?
3.下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。
课堂小结:
①理解随机事件的发生在大量重复试验下,呈现规律性;
②理解事件A出现的频率的意义,概率的概念
3.1.3 频率与概率
事件(1)、(4)、(6)是必然事件;
事件(2)、(9)、(10)是不可能事件;
事件(3)、(5)、(7)、(8)是随机事件.
指出下列事件是必然事件,不可能事件,还是随机事件:
(1)“抛一石块,下落”.
(2)“在标准大气压下且温度低于0℃时,冰融化”;
(3)“某人射击一次,中靶”;
(4)“如果a,b都是实数,则a+b=a+b;”;
(5)“将一枚硬币抛掷4次出现两次正面和两次反面”;
(6)“导体通电后,发热”;
(7)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(8)“某电话机在1分钟内收到2次呼叫”;
(9)“没有水份,种子能发芽”;
(10)“在常温下,焊锡熔化”.
问:
随机事件发生或者不发生是
不是没有任何规律呢?
第四步:找出掷硬币时“正面朝上”这个事件
发生的规律性。
试验者 试验次数
正面朝上的次数
正面朝上的比例
棣莫佛 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
频数:在相同的条件S下重复n次试验,观察
某一事件A是否出现,称n次试验中事 件A出现的次数 nA 为事件A出现的频数。
频率:事件A出现的比例 为事
件A出现的频率。
(三)频数与频率
试验者 试验次数
正面朝上的频数
正面朝上的频率
棣莫佛 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
(四)随机事件A的概率
对于给定的随机事件A,如 果随着试验次数的增加,事件A发生的频率fn(A) 稳定在某个常数附近,把这个常数记作P(A),称为事件A的概率,简称为A 的概率。
例如:P(正面朝上)=
0.5
P(反面朝上)=
0.5
不可能事件的概率为
必然事件的概率为
0
1
研究随机现象,不仅关心试验中会出现哪些事件,更重要的是想知道事件出现的可能性大小,也就是事件的概率.
概率是随机事件
发生可能性大小
的度量
事件发生的可能性
越大,概率就
越大!
思考:随机事件A在重复试验中出现的
频率 是不是不变的?随机事件A的概
率是不是不变的?它们之间有什么区别与
联系?
(1)大量重复进行同一试验时,随机事件发生与否呈现出规律性:频率总在P(A)附近摆动,当试验次数越多时,摆动幅度越小。
(2)0≤P(A)≤1,不可能事件的概率为0,必然事件的概率为1,随机事件的概率大于0而小于1。
(3)在实际问题中,通常随机事件的概率未知,常用频率作为它的估计值。
例2 某射手在同一条件下进行射击,结果如下表所示:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是什么?
分析:事件A出现的频数nA与试验次数n的比值即为事件A的频率,当事件A发生的频率fn(A)稳定在某个常数上时,这个常数即为事件A的概率。
解:(1)表中依次填入的数据为:0.80,0.95,0.88,0.92,0.89,0.91.
(2)由于频率稳定在常数0.89,所以这个射手击一次,击中靶心的概率约是0.89。
概率实际上是频率的科学抽象,
求某事件的概率可以通过求该事件
的频率而得之
2.某人进行打靶练习,共射击10次,其中有2次中10环,有3次环中9环,有4次中8环,有1次未中靶,试计算此人中靶的频率,假设此人射击1次,试问中靶的频率约为多大?中10环的概率约为多大?
1.一个地区从某年起几年之内的新生儿数及其中男婴数如下:
时间范围 1年内 2年内 3年内 4年内
新生婴儿数 5544 9607 13520 17190
男婴数 2883 4970 6994 8892
男婴出生的频率
(1)填写表中男婴出生的频率(结果保留到小数点后第3位);
(2)这一地区男婴出生的概率约是多少?
练习:
自我评价与课堂练习:
1.将一枚硬币向上抛掷10次,其中正面向上恰有5次是( )
A.必然事件 B.随机事件
C.不可能事件 D.无法确定
2.下列说法正确的是( )
A.任一事件的概率总在(0.1)内
B.不可能事件的概率不一定为0
C.必然事件的概率一定为1
D.以上均不对
每批粒数 2 5 10 70 130 700 1500 2000 3000
发芽的粒数 2 4 9 60 116 282 639 1339 2715
发芽的频率
(1)完成上面表格:
(2)该油菜子发芽的概率约是多少?
4.生活中,我们经常听到这样的议论:“天气预报说昨天降水概率为90%,结果根本一点雨都没下,天气预报也太不准确了。”学了概率后,你能给出解释吗?
3.下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。
课堂小结:
①理解随机事件的发生在大量重复试验下,呈现规律性;
②理解事件A出现的频率的意义,概率的概念
