1.2.2《集合的运算》课件(1)(新人教B版必修1)
文档属性
| 名称 | 1.2.2《集合的运算》课件(1)(新人教B版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 411.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-25 17:17:53 | ||
图片预览








文档简介
(共68张PPT)
1.2.2 集合的运算
知识整合
1.交集
对于两个给定的集合A、B,由属于A又属于B的所有元素所构成的集合,叫做A和B的________,记作________.
2.并集
一般地,对于两个给定的集合A、B,由两个集合的所有元素构成的集合,叫做A与B的________,记作A∪B.
3.全集
在研究集合与集合之间的关系时,如果________,那么称这个给定的集合为全集,通常用U表示.
特别警示:(1)全集决定了我们所研究的其他集合都是它的子集;(2)全集选择的不同,则运算的结果就有可能不同.
4.补集
如果给定集合A是全集U的一个子集,由________,叫做A在全集U中的补集,记作 UA.
5.交集的运算性质
对于任何集合A、B,有
(1)A∩B=B∩A;
(2)A∩A=________;
(3)A∩ =________;
(4)A∩B________A,A∩B________B;
(5)A∩B=A ________.
6.并集的运算性质
(1)A∪B=B∪A;
(2)A∪A=________;
(3)A∪ =________;
(4)A∪B________A,A∪B________B;
(5)A∪B=B ________.
7.交集、并集、补集的关系
A∩( UA)= ;A∪( UA)=U.
8.常见结论
(1)A∩B=A A B;A∪B=A A B;
(2)A∪( UA)=U;A∩( UA)= .
9.经验公式
(1) U(A∪B)=( UA)∩( UB); U(A∩B)=
( UA)∪( UB);
(2)card(A∪B)=card(A)+card(B)-card(A∩B)(其中card(A)表示集合A中的元素的个数).
对于(1)可理解:“并之补”等于“补之交”,“交之补”等于“补之并”.可通过Venn图加以记忆.
答案:1.交集 A∩B 2.并集
3.所要研究的集合都是某一给定集合的子集
4.U中不属于A的所有元素构成的集合
5.A A B
6.A A A B
名师解答
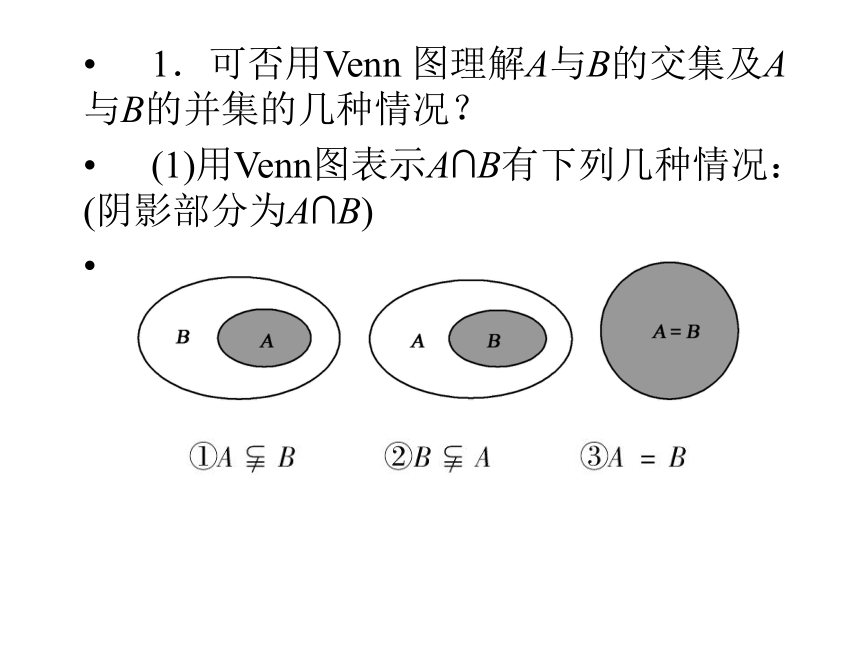
1.可否用Venn 图理解A与B的交集及A与B的并集的几种情况?
(1)用Venn图表示A∩B有下列几种情况:(阴影部分为A∩B)
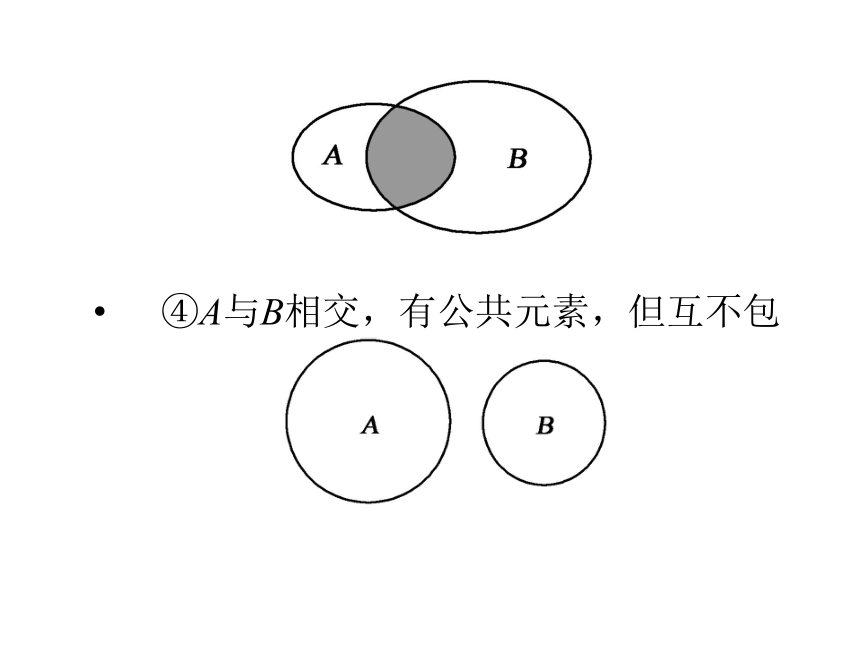
④A与B相交,有公共元素,但互不包含
⑤A与B分离,无公共元素
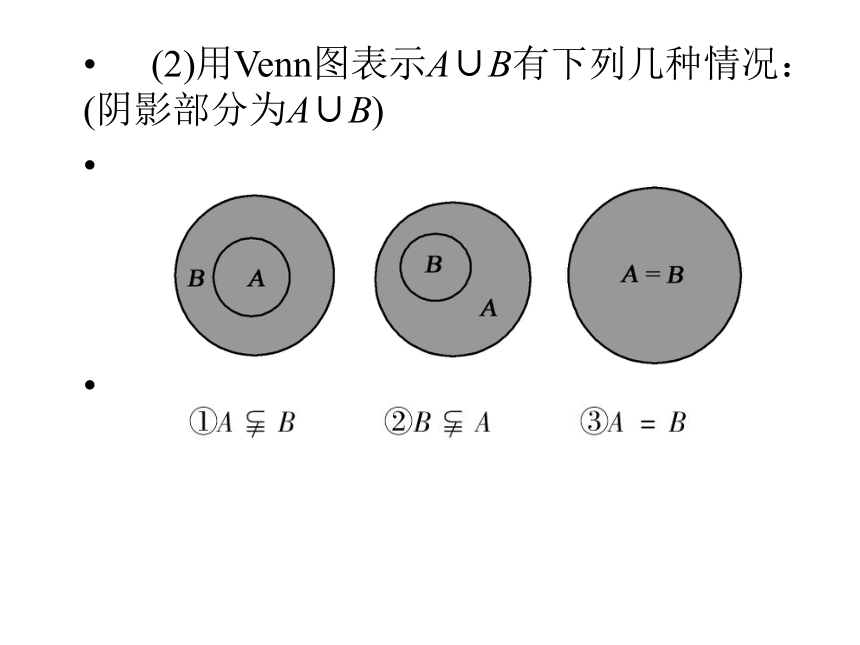
(2)用Venn图表示A∪B有下列几种情况:(阴影部分为A∪B)
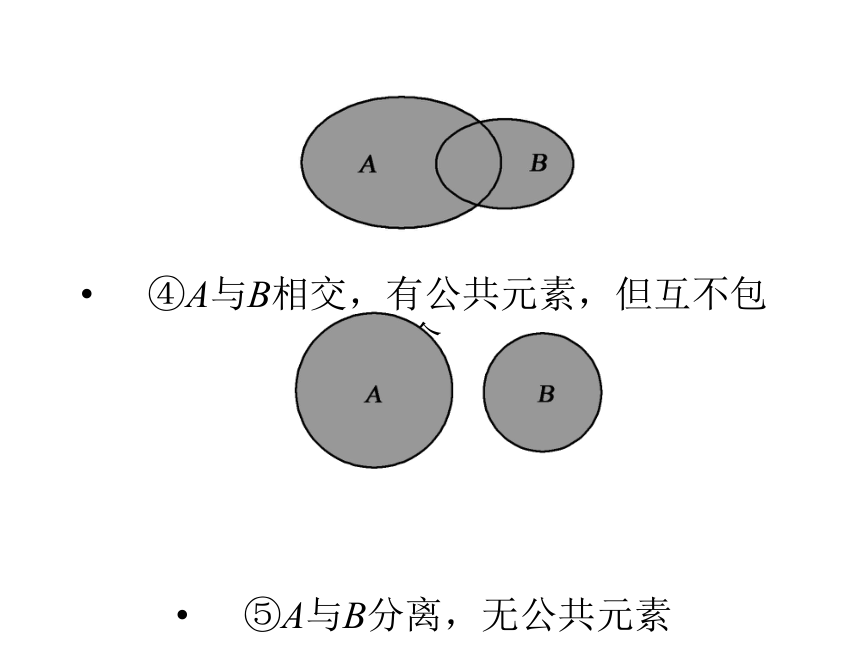
④A与B相交,有公共元素,但互不包含
⑤A与B分离,无公共元素
2.设集合U为全集,集合A,B是全集U的子集,则有以下两个重要结论:
U(A∩B)= UA∪ UB
U(A∪B)= UA∩ UB.
这两个结论,可否通过Venn图清楚明了地表示出来呢?
(1)用Venn图表示: U(A∩B)= UA∪ UB.
(2)用Venn图表示: U(A∪B)= UA∩ UB.
深入学习
答案:(1)C (2)A
分析:注意集合M、P中的元素,确定出M、P,再求M∩P.
(1)解法一:M中x+1≥0,
∴x≥-1,即M={x|x≥-1}.
P中x-3≤0,
∴x≤3,即P={x|x≤3}.
∴M∩P={x|-1≤x≤3},故选C.
解法二:∵M∩P的元素不是(x,y),∴排除A.
比较B与C,取x=-1,∵-1∈M,-1∈P.
∴-1∈(M∩P),∴排除B.
比较C与D,取x=-2,
∵-2 M,∴排除D.故选C.
评析:解法一是直接法,求交集、并集时一般需先具体确定集合再求;解法二是排除法,即抓住选择项之间的差异,采用取特殊值或举反例等办法排除错选择项,达到去伪存真的目的,此法对求解选择题很有效.
评析:本节重点是交集、并集的概念,正确理解概念是进行集合间的交、并运算的关键.
关于定义需注意:
①A∪B中“或”的意义与日常用语中的“或”的意义不尽相同,用它连接的并列成分之间不一定是互相排斥的,“x∈A,或x∈B”包括下列三种情况:①x∈A,但x B;②x∈B,但x A;③x∈A,且x∈B.
②因为并不是任何两个集合总有公共元素,当A与B没有公共元素时,不能说A与B的交集不存在,而应说A∩B= .
变式训练 1 集合A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-mx+2=0},已知A∪B=A,A∩C=C,求实数a、m的值.
解:∵A∪B=A,∴B A.又A∩C=C,∴C A.
∵A={x|x2-3x+2=0}={1,2},
B={x|x2-ax+(a-1)=0}
={x|(x-a+1)(x-1)=0},
又∵B A,
∴a-1=2或a-1=1.即a=3或a=2.
当a=3时,B={1,2};当a=2时,B={1}.
题型二 集合的运算
【例2】 设U=R,已知集合A={x|-5(3)A∪( UB);(4)B∩( UA);(5)( UA)∩
( UB).
分析:本题是不等式问题,凡不等式中的交、并、补问题,可以画数轴解决.
解:如下图.
(1)A∩B={x|0≤x<5}.
(2)A∪B={x|-5(3)如下图.
UB={x|x<0,或x≥7},
∴A∪( UB)={x|x<5,或x≥7}.
(4)如下图.
UA={x|x≤-5,或x≥5},
B∩( UA)={x|5≤x<7}.
(5)解法一:∵ UB={x|x<0,或x≥7},
UA={x|x≤-5,或x≥5}.∴如下图.
( UA)∩( UB)={x|x≤-5,或x≥7}.
解法二:( UA)∩( UB)= U(A∪B)
={x|x≤-5,或x≥7}.
评析:(1)数轴法的特点是简单直观,因此,要注意将数轴画出来,只有对数轴的运用达到熟练掌握了,就可以不必画数轴了,但也应在草稿上或自己的头脑中画出数轴,避免出错.
(2)要注意各个端点的画法:能取到端点的值时,用实心的点在数轴上表示;取不到端点的值时,用空心的圈在数轴上表示.
(3)一定要注意A∪ UA=U,A∩ UA= ,从而决定端点的去留.
题型三 利用韦恩图解题
【例3】 已知全集U={不大于20的质数},M、N是U的子集,且满足M∩( UN)={3,5},( UM)∩N={7,19},( UM)∩( UN)={2,17},求M,N.
解:∵M∩( UN)={3,5},
∴3∈M,5∈M,3 N,5 N.
又∵( UM)∩N={7,19},
∴7 M,19 M,7∈N,19∈N.
又∵( UM)∩( UN)= U(M∪N)={2,17},
∴2 M,2 N,17 M,17 N.
由以上分析,画出图.
又∵11 U(M∪N),
∴11∈M∪N.
∵11 M∩( UN),
∴11∈N,或11∈M∩N.
又∵11 ( UM)∩N,
∴11∈M,或11∈M∩N.
11既不在M∩( UN)中,同时又不在( UM)∩N中,所以即11∈M∩N.
同理,13∈M∩N.
∴M={3,5,11,13},N={7,11,13,19}.
评析:对于一些与数集有关的问题,直接凭空去想,很容易陷入误区,理不清头绪.如果采用韦恩图来分析问题,则题目会变得很直观,很容易理清思路,使问题获解.
变式训练 3 某班举行数理化竞赛,每人至少参加一科,已知参加数学竞赛的有27人,参加物理竞赛的有25人,参加化学竞赛的有27人,其中参加数学、物理两科的有10人,参加物理、化学两科的有7人,参加数学、化学两科的有11人,而参加数、理、化三科的有4人,求出全班人数.
分析:本题考查集合的运算,解题的关键是把文字语言转化成集合语言,借助于韦恩图的直观性把它表示出来,再根据集合中元素的互异性求出问题的解.
解:设参加数学、物理、化学三科竞赛的同学组成的集合分别为A、B、C,由题意可知A、B、C 三集合中元素个数分别为27、25、27,A∩B、B∩C、A∩C、A∩B∩C 的元素个数分别为10、7、11、4.
画出韦恩图,如图
可知全班人数为
10+13+12+6+4+7+3=55(人).
评析:(1)能正确使用一些集合符号把文字语言转化成集合语言、图形语言是我们把实际问题转化成数学问题的重要一步,它实现了实际问题向数学问题的转化.
(2)一般地,用card(A)、card(B)、card(C)分别表示集合A、B、C 中元素的个数,则有card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(A∩C)+card(A∩B∩C).
题型四 利用集合运算性质求参数的取值范围
【例4】 已知集合A={x|x2-4x+3=0},B={x|x2-ax-1+a=0},C={x|x2-mx+1=0},且A∪B=A,A∩C=C,求a、m的取值或取值范围.
分析:可知求集合A,再由A∪B=A B A,A∩C=C C A,然后根据方程根的情况进行讨论.
解:A={1,3},B={x|(x-1)(x+1-a)=0}.
∵A∪B=A,∴B A.∴a-1=3,或a-1=1.
∴a=4,或a=2.又A∩C=C,∴C A.
若C= ,则Δ=m2-4<0,∴-2若1∈C,则12-m+1=0,
∴m=2.此时C={1},A∩C=C.
评析:分类讨论在中学数学中有着极其重要的地位,在本章应用广泛,本题中易犯的错误是忽略对C≠ 的讨论.
变式训练 4 已知集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求实数a的值;
(2) ?A∩B,A∩C= ,求实数a的值.
分析:集合A,B,C的关系比较明确,从代数角度看,它们分别是方程x2-ax+a2-19=0,x2-5x+6=0和x2+2x-8=0的解集.由于集合A所对应的方程含有字母,因此本题宜先考虑的B,C再由(1)中A∩B=B∪A,(2)中 ?
A∩B,A∩C= 等条件出发,确定a的值.
评析:对于(1),必须理解A∩B=A∪B的意义(由A A∩B)=A∪B B A B,B A∩B=A∪B A B A,所以A=B);对于(2)关键在于抓住空集这个特殊集合的含义和性质,即由 ?A∩B A∩B≠ .
整体探究解读
题型一 集合的运算问题
集合的基本运算广泛地用于函数、方程、不等式、三角函数、解析几何等知识中,在高考中占有相当重要的地位,要熟练掌握交、并、补的含义及运算性质,学会用Venn图、数轴工具来解决问题.
【例1】 已知集合P={x|x=a2+4a+1,a∈R},Q={y|y=-b2+2b+3,b∈R},求P∩Q和P∪ RQ.
分析:集合P,Q分别是指对应的自变量a,b在实数范围内变化时,函数值的变化范围.
解:因为x=a2+4a+1=(a+2)2-3≥-3,所以P={x|x≥-3};
又因为y=-b2+2b+3=-(b-1)2+4≤4,所以Q={y|y≤4}.
利用数轴表示可知,P∩Q={x|-3≤x≤4}(如下图(1));
又因为 RQ={y|y>4},所以P∪ RQ=P={x|x≥-3}(如下图(2)).
评析:(1)在求集合的交集、并集、补集时,应首先求出各集合.本题中,虽然表示集合元素的字母不同,但它们都是数集.
(2)在求集合的补集时要注意边界.
(3)求数集的交集、并集、补集往往借助于数轴.
【例2】 设A={x|a≤x≤a+3},B={x|x<-1,或x>5},当a为何值时(1)A∩B= ;(2)A∩B≠ ;(3)A∩B=A;(4)A∪ RB= RB.
(2)由补集的定义可知,
A∩B≠ 的反面就是A∩B= .
∴当a<-1,或a>2时,A∩B≠ .
(3)∵A∩B=A,∴A B.
由下图得,a+3<-1,或a>5.
即a<-4,或a>5时,A∩B=A.
题型二 解探索性问题
【例3】 已知A={(x,y)|x=n,y=an+b,n∈Z},B={(x,y)|x=m,y=3m2+15,m∈Z};C={(x,y)|x2+y2≤144},问是否存在实数a,b使得(1)A∩B≠ ,(2)(a,b)∈C同时成立?
分析:假设存在a,b,使得(1)成立,得到a与b的关系后与a2+b2≤144联立,然后讨论联立的不等式组.
评析:①此解法中“Δ≥0”仅是一个方程有解的必要条件,也就是说Δ≥0只能保证直线与抛物线有公共点,但这个公共点不一定是整数点,进而再利用另一个条件,由于求得的a,b不能使两曲线的交点为整数点,所以符合题意的a,b就不存在了.
②解答探索性数学问题,凡是涉及“是否存在”,“是否具有某种性质”等这一类的未定结论的讨论式探索性问题,我们总是先假定结论成立,进而进行演绎推理,在推导过程中,若出现矛盾,即可否定我们的假设,则问题的另一面成立;如果推导过程流畅,没有受阻,没有矛盾成立,一直能推导到符合已知的真理(公理、定理等)或已知条件,这时我们说假设存在.
题型三 用“正难则反”的策略解题
“正难则反”策略是指某一类问题从正面解决比较困难时,我们可以反面入手解决.这种“正难则反”的解题方法,运用的就是补集思想,设全集为U,求子集A,若直接求A困难,可先求 UA,再由 U( UA)=A求A.
【例4】 若三个方程x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实数解,求实数a的取值范围.
分析:此题若从正面入手,需对各种可能情况一一讨论,非常繁琐,若考虑反面,则只有一种情况:三个方程都没有实数解,利用判别式去求解,然后取补集即可.
评析:一般地,如果一个数学问题从正面入手困难可作逆向思考则常可奏效.如含有“至多”、“至少”等条件的题目,不要忘记取其补集.
1.进行集合的运算时应当注意:(1)勿忘对空集情形的讨论;(2)勿忘集合中元素的互异性;(3)对于集合A的补集进行运算,勿忘A必须是全集的子集;(4)对于含参数(或特定系数)的集合问题,勿忘对所求数值进行合理取舍.
2.在集合运算过程中应力求做到“三化”:
(1)意义化:即首先分清集合的类型,是表示数集、点集,还是某类图形?是表示函数的自变量的取值范围,或因变量的取值范围,还是表示方程或不等式的解集?
(2)具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
(3)直观化:借助数轴、直角坐标平面、韦恩图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.
【例5】 已知集合A={x|x2-4ax+2a+6=0},B={x|x<0},若A∩B≠ ,求a的取值范围.
解:由B={x|x<0},A∩B≠ 可知,方程x2-4ax+2a+6=0至少有一个负根,因此本题要分:有两个负根、一负根一零根、一负根一正根这三种情况求解,比较麻烦,这时,我们不妨考虑问题的反面:方程x2-4ax+2a+6=0没有负根的情形.
评析:(1)对于一些解题过程繁琐,难以从正面解决的问题,不妨从问题的反面入手,探求已知和未知的联系,用间接的方法将问题解决,我们称这种解决问题的策略为“正难则反”的策略,其实质是运用了“补集思想”.
(2)由于 UA是A的补集,因此在解题时,遇到比较困难的问题,可以转化为求问题的反面,采用间接的方法将问题解决.
题型四 数学在日常生活中的应用
【例6】 某地对农户抽样调查,结果如下:电冰箱拥有率为49%,电视机拥有率为85%,洗衣机拥有率为44%,至少拥有上述三种电器中两种以上的占63%,三种电器齐全的为25%,那么一种电器也没有的相对贫困户所占比例为 ( )
A.10% B.12%
C.15% D.27%
答案:A
分析:这是一个小型应用题,把各种人群看做集合,本题就是已知全集元素个数,求其某个子集的元素个数,可借助Venn图解决.
解:不妨设调查了100户农户,U={被调查的100户农户},A={100户中拥有电冰箱的农户},B={100户中拥有电视机的农户},C={100户中拥有洗衣机的农户},由图知,A∪B∪C的元素个数为49+85+44-63-25=90.
∴ U(A∪B∪C)的元素个数为100-90=10.
故选A.
评析:善于用数学中的集合知识解决日常生活中的实际问题,有时可以借助韦恩图.
分析:首先假设这样的a存在,则A∪B= 成立,由此推出A=B= ,则一元二次方程的判别式Δ<0,照此计算下去,结果就会显露出来.
评析:本题有两个关键点:其一,由A∪B= 得A= 且B= ,因此,得到由判别式构成的不等式组.其二,不等式组的解法,虽然在后面我们还将专门学习“一元二次不等式解法”,但根据实数的“同号相乘得正,异号相乘得负”的性质,我们现在也能解部分一元二次不等式,但要特别注意何时取交集,何时取并集.
【例8】 我们知道,如果集合A S,那么S的子集A的补集为 SA={x|x∈S,且x A}.类似地,对于集合A、B,我们把集合{x|x∈A,且x B}叫做集合A与B的差集,记作A-B.例如,A={1,2,3,4,5},B={4,5,6,7,8},则有A-B={1,2,3},B-A={6,7,8},据此,试回答下列问题:
(1)S是高一(1)班全体同学的集合,A是高一(1)班全体女同学的集合,求S—A及 SA;
(2)在下图中用阴影表示集合A-B;
(3)如果A-B= ,那么集合A与B之间具有怎样的关系?
分析:本题是一道信息题,要求阅读理解题目中给出的信息,并给出解答.考查同学们认知新知识的能力.
解:(1)S-A= SA={x|x是高一(1)班的全体男同学}.
(2)如下图中阴影部分所示.
(3)A B.
1.2.2 集合的运算
知识整合
1.交集
对于两个给定的集合A、B,由属于A又属于B的所有元素所构成的集合,叫做A和B的________,记作________.
2.并集
一般地,对于两个给定的集合A、B,由两个集合的所有元素构成的集合,叫做A与B的________,记作A∪B.
3.全集
在研究集合与集合之间的关系时,如果________,那么称这个给定的集合为全集,通常用U表示.
特别警示:(1)全集决定了我们所研究的其他集合都是它的子集;(2)全集选择的不同,则运算的结果就有可能不同.
4.补集
如果给定集合A是全集U的一个子集,由________,叫做A在全集U中的补集,记作 UA.
5.交集的运算性质
对于任何集合A、B,有
(1)A∩B=B∩A;
(2)A∩A=________;
(3)A∩ =________;
(4)A∩B________A,A∩B________B;
(5)A∩B=A ________.
6.并集的运算性质
(1)A∪B=B∪A;
(2)A∪A=________;
(3)A∪ =________;
(4)A∪B________A,A∪B________B;
(5)A∪B=B ________.
7.交集、并集、补集的关系
A∩( UA)= ;A∪( UA)=U.
8.常见结论
(1)A∩B=A A B;A∪B=A A B;
(2)A∪( UA)=U;A∩( UA)= .
9.经验公式
(1) U(A∪B)=( UA)∩( UB); U(A∩B)=
( UA)∪( UB);
(2)card(A∪B)=card(A)+card(B)-card(A∩B)(其中card(A)表示集合A中的元素的个数).
对于(1)可理解:“并之补”等于“补之交”,“交之补”等于“补之并”.可通过Venn图加以记忆.
答案:1.交集 A∩B 2.并集
3.所要研究的集合都是某一给定集合的子集
4.U中不属于A的所有元素构成的集合
5.A A B
6.A A A B
名师解答
1.可否用Venn 图理解A与B的交集及A与B的并集的几种情况?
(1)用Venn图表示A∩B有下列几种情况:(阴影部分为A∩B)
④A与B相交,有公共元素,但互不包含
⑤A与B分离,无公共元素
(2)用Venn图表示A∪B有下列几种情况:(阴影部分为A∪B)
④A与B相交,有公共元素,但互不包含
⑤A与B分离,无公共元素
2.设集合U为全集,集合A,B是全集U的子集,则有以下两个重要结论:
U(A∩B)= UA∪ UB
U(A∪B)= UA∩ UB.
这两个结论,可否通过Venn图清楚明了地表示出来呢?
(1)用Venn图表示: U(A∩B)= UA∪ UB.
(2)用Venn图表示: U(A∪B)= UA∩ UB.
深入学习
答案:(1)C (2)A
分析:注意集合M、P中的元素,确定出M、P,再求M∩P.
(1)解法一:M中x+1≥0,
∴x≥-1,即M={x|x≥-1}.
P中x-3≤0,
∴x≤3,即P={x|x≤3}.
∴M∩P={x|-1≤x≤3},故选C.
解法二:∵M∩P的元素不是(x,y),∴排除A.
比较B与C,取x=-1,∵-1∈M,-1∈P.
∴-1∈(M∩P),∴排除B.
比较C与D,取x=-2,
∵-2 M,∴排除D.故选C.
评析:解法一是直接法,求交集、并集时一般需先具体确定集合再求;解法二是排除法,即抓住选择项之间的差异,采用取特殊值或举反例等办法排除错选择项,达到去伪存真的目的,此法对求解选择题很有效.
评析:本节重点是交集、并集的概念,正确理解概念是进行集合间的交、并运算的关键.
关于定义需注意:
①A∪B中“或”的意义与日常用语中的“或”的意义不尽相同,用它连接的并列成分之间不一定是互相排斥的,“x∈A,或x∈B”包括下列三种情况:①x∈A,但x B;②x∈B,但x A;③x∈A,且x∈B.
②因为并不是任何两个集合总有公共元素,当A与B没有公共元素时,不能说A与B的交集不存在,而应说A∩B= .
变式训练 1 集合A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-mx+2=0},已知A∪B=A,A∩C=C,求实数a、m的值.
解:∵A∪B=A,∴B A.又A∩C=C,∴C A.
∵A={x|x2-3x+2=0}={1,2},
B={x|x2-ax+(a-1)=0}
={x|(x-a+1)(x-1)=0},
又∵B A,
∴a-1=2或a-1=1.即a=3或a=2.
当a=3时,B={1,2};当a=2时,B={1}.
题型二 集合的运算
【例2】 设U=R,已知集合A={x|-5
( UB).
分析:本题是不等式问题,凡不等式中的交、并、补问题,可以画数轴解决.
解:如下图.
(1)A∩B={x|0≤x<5}.
(2)A∪B={x|-5
UB={x|x<0,或x≥7},
∴A∪( UB)={x|x<5,或x≥7}.
(4)如下图.
UA={x|x≤-5,或x≥5},
B∩( UA)={x|5≤x<7}.
(5)解法一:∵ UB={x|x<0,或x≥7},
UA={x|x≤-5,或x≥5}.∴如下图.
( UA)∩( UB)={x|x≤-5,或x≥7}.
解法二:( UA)∩( UB)= U(A∪B)
={x|x≤-5,或x≥7}.
评析:(1)数轴法的特点是简单直观,因此,要注意将数轴画出来,只有对数轴的运用达到熟练掌握了,就可以不必画数轴了,但也应在草稿上或自己的头脑中画出数轴,避免出错.
(2)要注意各个端点的画法:能取到端点的值时,用实心的点在数轴上表示;取不到端点的值时,用空心的圈在数轴上表示.
(3)一定要注意A∪ UA=U,A∩ UA= ,从而决定端点的去留.
题型三 利用韦恩图解题
【例3】 已知全集U={不大于20的质数},M、N是U的子集,且满足M∩( UN)={3,5},( UM)∩N={7,19},( UM)∩( UN)={2,17},求M,N.
解:∵M∩( UN)={3,5},
∴3∈M,5∈M,3 N,5 N.
又∵( UM)∩N={7,19},
∴7 M,19 M,7∈N,19∈N.
又∵( UM)∩( UN)= U(M∪N)={2,17},
∴2 M,2 N,17 M,17 N.
由以上分析,画出图.
又∵11 U(M∪N),
∴11∈M∪N.
∵11 M∩( UN),
∴11∈N,或11∈M∩N.
又∵11 ( UM)∩N,
∴11∈M,或11∈M∩N.
11既不在M∩( UN)中,同时又不在( UM)∩N中,所以即11∈M∩N.
同理,13∈M∩N.
∴M={3,5,11,13},N={7,11,13,19}.
评析:对于一些与数集有关的问题,直接凭空去想,很容易陷入误区,理不清头绪.如果采用韦恩图来分析问题,则题目会变得很直观,很容易理清思路,使问题获解.
变式训练 3 某班举行数理化竞赛,每人至少参加一科,已知参加数学竞赛的有27人,参加物理竞赛的有25人,参加化学竞赛的有27人,其中参加数学、物理两科的有10人,参加物理、化学两科的有7人,参加数学、化学两科的有11人,而参加数、理、化三科的有4人,求出全班人数.
分析:本题考查集合的运算,解题的关键是把文字语言转化成集合语言,借助于韦恩图的直观性把它表示出来,再根据集合中元素的互异性求出问题的解.
解:设参加数学、物理、化学三科竞赛的同学组成的集合分别为A、B、C,由题意可知A、B、C 三集合中元素个数分别为27、25、27,A∩B、B∩C、A∩C、A∩B∩C 的元素个数分别为10、7、11、4.
画出韦恩图,如图
可知全班人数为
10+13+12+6+4+7+3=55(人).
评析:(1)能正确使用一些集合符号把文字语言转化成集合语言、图形语言是我们把实际问题转化成数学问题的重要一步,它实现了实际问题向数学问题的转化.
(2)一般地,用card(A)、card(B)、card(C)分别表示集合A、B、C 中元素的个数,则有card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(A∩C)+card(A∩B∩C).
题型四 利用集合运算性质求参数的取值范围
【例4】 已知集合A={x|x2-4x+3=0},B={x|x2-ax-1+a=0},C={x|x2-mx+1=0},且A∪B=A,A∩C=C,求a、m的取值或取值范围.
分析:可知求集合A,再由A∪B=A B A,A∩C=C C A,然后根据方程根的情况进行讨论.
解:A={1,3},B={x|(x-1)(x+1-a)=0}.
∵A∪B=A,∴B A.∴a-1=3,或a-1=1.
∴a=4,或a=2.又A∩C=C,∴C A.
若C= ,则Δ=m2-4<0,∴-2
∴m=2.此时C={1},A∩C=C.
评析:分类讨论在中学数学中有着极其重要的地位,在本章应用广泛,本题中易犯的错误是忽略对C≠ 的讨论.
变式训练 4 已知集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求实数a的值;
(2) ?A∩B,A∩C= ,求实数a的值.
分析:集合A,B,C的关系比较明确,从代数角度看,它们分别是方程x2-ax+a2-19=0,x2-5x+6=0和x2+2x-8=0的解集.由于集合A所对应的方程含有字母,因此本题宜先考虑的B,C再由(1)中A∩B=B∪A,(2)中 ?
A∩B,A∩C= 等条件出发,确定a的值.
评析:对于(1),必须理解A∩B=A∪B的意义(由A A∩B)=A∪B B A B,B A∩B=A∪B A B A,所以A=B);对于(2)关键在于抓住空集这个特殊集合的含义和性质,即由 ?A∩B A∩B≠ .
整体探究解读
题型一 集合的运算问题
集合的基本运算广泛地用于函数、方程、不等式、三角函数、解析几何等知识中,在高考中占有相当重要的地位,要熟练掌握交、并、补的含义及运算性质,学会用Venn图、数轴工具来解决问题.
【例1】 已知集合P={x|x=a2+4a+1,a∈R},Q={y|y=-b2+2b+3,b∈R},求P∩Q和P∪ RQ.
分析:集合P,Q分别是指对应的自变量a,b在实数范围内变化时,函数值的变化范围.
解:因为x=a2+4a+1=(a+2)2-3≥-3,所以P={x|x≥-3};
又因为y=-b2+2b+3=-(b-1)2+4≤4,所以Q={y|y≤4}.
利用数轴表示可知,P∩Q={x|-3≤x≤4}(如下图(1));
又因为 RQ={y|y>4},所以P∪ RQ=P={x|x≥-3}(如下图(2)).
评析:(1)在求集合的交集、并集、补集时,应首先求出各集合.本题中,虽然表示集合元素的字母不同,但它们都是数集.
(2)在求集合的补集时要注意边界.
(3)求数集的交集、并集、补集往往借助于数轴.
【例2】 设A={x|a≤x≤a+3},B={x|x<-1,或x>5},当a为何值时(1)A∩B= ;(2)A∩B≠ ;(3)A∩B=A;(4)A∪ RB= RB.
(2)由补集的定义可知,
A∩B≠ 的反面就是A∩B= .
∴当a<-1,或a>2时,A∩B≠ .
(3)∵A∩B=A,∴A B.
由下图得,a+3<-1,或a>5.
即a<-4,或a>5时,A∩B=A.
题型二 解探索性问题
【例3】 已知A={(x,y)|x=n,y=an+b,n∈Z},B={(x,y)|x=m,y=3m2+15,m∈Z};C={(x,y)|x2+y2≤144},问是否存在实数a,b使得(1)A∩B≠ ,(2)(a,b)∈C同时成立?
分析:假设存在a,b,使得(1)成立,得到a与b的关系后与a2+b2≤144联立,然后讨论联立的不等式组.
评析:①此解法中“Δ≥0”仅是一个方程有解的必要条件,也就是说Δ≥0只能保证直线与抛物线有公共点,但这个公共点不一定是整数点,进而再利用另一个条件,由于求得的a,b不能使两曲线的交点为整数点,所以符合题意的a,b就不存在了.
②解答探索性数学问题,凡是涉及“是否存在”,“是否具有某种性质”等这一类的未定结论的讨论式探索性问题,我们总是先假定结论成立,进而进行演绎推理,在推导过程中,若出现矛盾,即可否定我们的假设,则问题的另一面成立;如果推导过程流畅,没有受阻,没有矛盾成立,一直能推导到符合已知的真理(公理、定理等)或已知条件,这时我们说假设存在.
题型三 用“正难则反”的策略解题
“正难则反”策略是指某一类问题从正面解决比较困难时,我们可以反面入手解决.这种“正难则反”的解题方法,运用的就是补集思想,设全集为U,求子集A,若直接求A困难,可先求 UA,再由 U( UA)=A求A.
【例4】 若三个方程x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实数解,求实数a的取值范围.
分析:此题若从正面入手,需对各种可能情况一一讨论,非常繁琐,若考虑反面,则只有一种情况:三个方程都没有实数解,利用判别式去求解,然后取补集即可.
评析:一般地,如果一个数学问题从正面入手困难可作逆向思考则常可奏效.如含有“至多”、“至少”等条件的题目,不要忘记取其补集.
1.进行集合的运算时应当注意:(1)勿忘对空集情形的讨论;(2)勿忘集合中元素的互异性;(3)对于集合A的补集进行运算,勿忘A必须是全集的子集;(4)对于含参数(或特定系数)的集合问题,勿忘对所求数值进行合理取舍.
2.在集合运算过程中应力求做到“三化”:
(1)意义化:即首先分清集合的类型,是表示数集、点集,还是某类图形?是表示函数的自变量的取值范围,或因变量的取值范围,还是表示方程或不等式的解集?
(2)具体化:具体求出相关集合中函数的自变量、因变量的范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.
(3)直观化:借助数轴、直角坐标平面、韦恩图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.
【例5】 已知集合A={x|x2-4ax+2a+6=0},B={x|x<0},若A∩B≠ ,求a的取值范围.
解:由B={x|x<0},A∩B≠ 可知,方程x2-4ax+2a+6=0至少有一个负根,因此本题要分:有两个负根、一负根一零根、一负根一正根这三种情况求解,比较麻烦,这时,我们不妨考虑问题的反面:方程x2-4ax+2a+6=0没有负根的情形.
评析:(1)对于一些解题过程繁琐,难以从正面解决的问题,不妨从问题的反面入手,探求已知和未知的联系,用间接的方法将问题解决,我们称这种解决问题的策略为“正难则反”的策略,其实质是运用了“补集思想”.
(2)由于 UA是A的补集,因此在解题时,遇到比较困难的问题,可以转化为求问题的反面,采用间接的方法将问题解决.
题型四 数学在日常生活中的应用
【例6】 某地对农户抽样调查,结果如下:电冰箱拥有率为49%,电视机拥有率为85%,洗衣机拥有率为44%,至少拥有上述三种电器中两种以上的占63%,三种电器齐全的为25%,那么一种电器也没有的相对贫困户所占比例为 ( )
A.10% B.12%
C.15% D.27%
答案:A
分析:这是一个小型应用题,把各种人群看做集合,本题就是已知全集元素个数,求其某个子集的元素个数,可借助Venn图解决.
解:不妨设调查了100户农户,U={被调查的100户农户},A={100户中拥有电冰箱的农户},B={100户中拥有电视机的农户},C={100户中拥有洗衣机的农户},由图知,A∪B∪C的元素个数为49+85+44-63-25=90.
∴ U(A∪B∪C)的元素个数为100-90=10.
故选A.
评析:善于用数学中的集合知识解决日常生活中的实际问题,有时可以借助韦恩图.
分析:首先假设这样的a存在,则A∪B= 成立,由此推出A=B= ,则一元二次方程的判别式Δ<0,照此计算下去,结果就会显露出来.
评析:本题有两个关键点:其一,由A∪B= 得A= 且B= ,因此,得到由判别式构成的不等式组.其二,不等式组的解法,虽然在后面我们还将专门学习“一元二次不等式解法”,但根据实数的“同号相乘得正,异号相乘得负”的性质,我们现在也能解部分一元二次不等式,但要特别注意何时取交集,何时取并集.
【例8】 我们知道,如果集合A S,那么S的子集A的补集为 SA={x|x∈S,且x A}.类似地,对于集合A、B,我们把集合{x|x∈A,且x B}叫做集合A与B的差集,记作A-B.例如,A={1,2,3,4,5},B={4,5,6,7,8},则有A-B={1,2,3},B-A={6,7,8},据此,试回答下列问题:
(1)S是高一(1)班全体同学的集合,A是高一(1)班全体女同学的集合,求S—A及 SA;
(2)在下图中用阴影表示集合A-B;
(3)如果A-B= ,那么集合A与B之间具有怎样的关系?
分析:本题是一道信息题,要求阅读理解题目中给出的信息,并给出解答.考查同学们认知新知识的能力.
解:(1)S-A= SA={x|x是高一(1)班的全体男同学}.
(2)如下图中阴影部分所示.
(3)A B.
同课章节目录
