等比数列前n项和(说课课件)
图片预览






文档简介
(共28张PPT)
新课标人教版课件系列
《高中数学》
必修5
2.5《等比数列的前n项和》
审校:王伟
教学目标
知识与技能:掌握等比数列的前n项和公式,并用公式解决实际问题
过程与方法:由研究等比数列的结构特点推导出等比数列的前n项和公式
情态与价值:从“错位相减法”这种算法中,体会“消除差别”,培养化简的能力
(二)教学重、难点
重点:使学生掌握等比数列的前n项和公式,用等比数列的前n项和公式解决实际问题
难点:由研究等比数列的结构特点推导出等比数列的前n项和公式
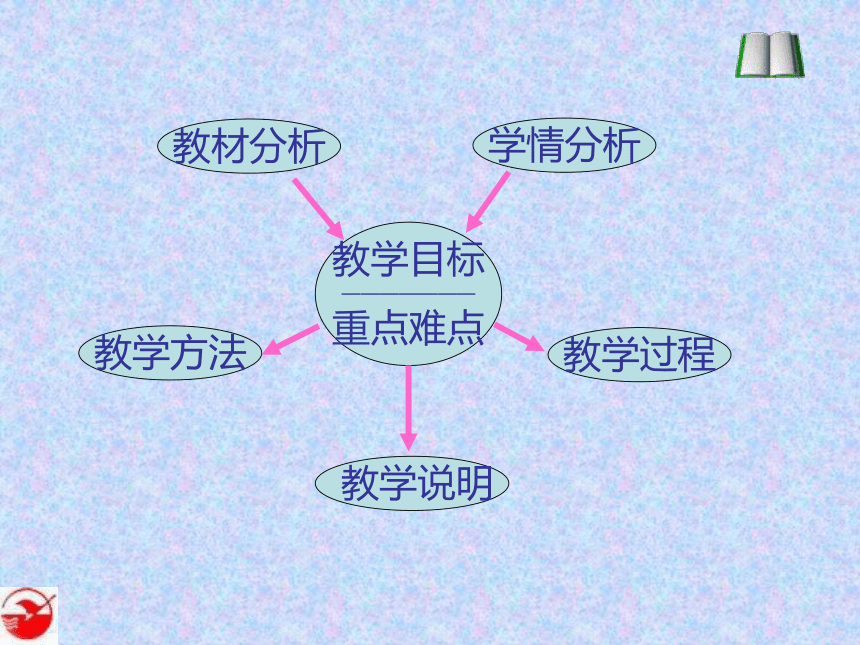
教材分析
教学方法
学情分析
教学说明
教学目标
———————
重点难点
教学过程
有助于提升学生的创新思维和探索精神,是培养学生应用意识和数学能力的良好载体.
等比数列的前n项和是“等差数列及其前n项和”与“等比数列”内容的延续、与函数等知识有着密切的联系,又为学习“数列的极限”等内容作准备,具有承上启下的作用.
教材分析
学情分析
认知
情感
能力
掌握等差数列和等比数列的有关知识.
初步具备运用知识解决问题的能力;但对知识的整合能力、问题的探究能力及思维的严密性上还需要进一步培养和提高.
学习兴趣比较浓,表现欲较强,但合作交流的意识等方面尚有待加强.
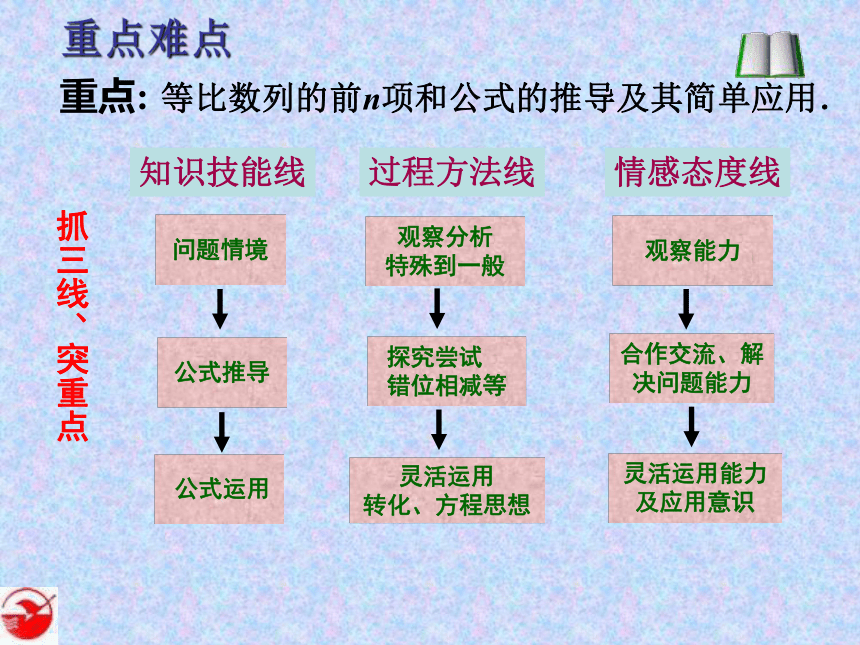
重点难点
重点:
等比数列的前n项和公式的推导及其简单应用.
知识技能线
情感态度线
过程方法线
观察分析
特殊到一般
灵活运用能力及应用意识
问题情境
公式推导
公式运用
探究尝试
错位相减等
灵活运用
转化、方程思想
突重点
观察能力
合作交流、解决问题能力
抓三线、
重点难点
难点:
等比数列的前n项和公式的推导.
抓两点、破难点
情感、思维的兴奋点
知识选择的切入点
◆学生认知
◆知识特点
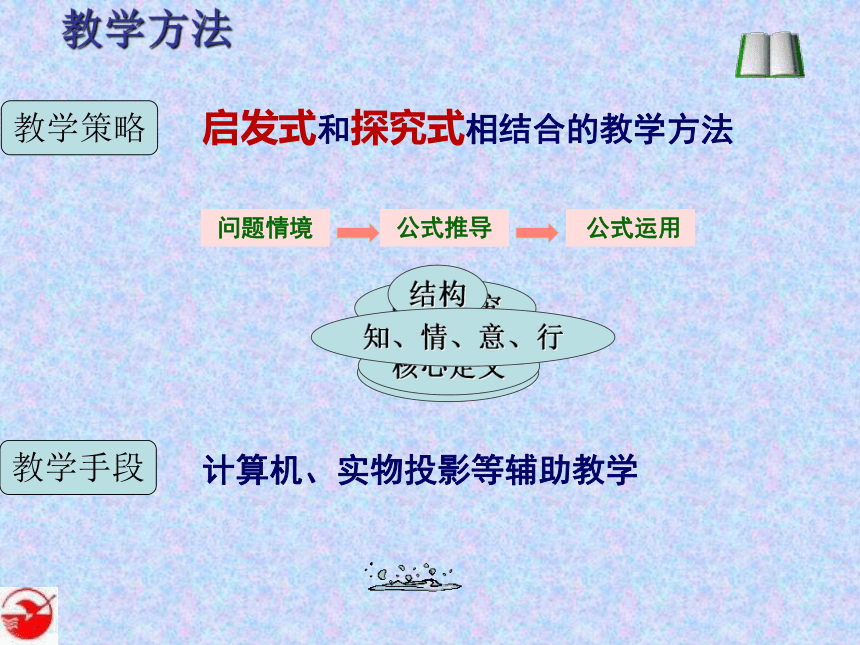
教学方法
问题情境
公式推导
公式运用
启发式和探究式相结合的教学方法
计算机、实物投影等辅助教学
教学策略
教学手段
合作探究
自主探究
结构
核心定义
知、情、意、行
教学目标
————————
重点难点
教学过程
升
练
释
探
引
过程分析
创设情境
探究问题
辨析质疑
巩固提高
反思提炼
延
作业布置
引
探
升
练
释
延
引
高老庄集团
高老庄
哈哈,我是CEO了……
情
境
设
置
生
活
化
西游记后传
过程分析
周转不灵……
引
探
升
练
释
延
引
情
境
设
置
生
活
化
西游记后传
过程分析
西游记后传
No problem!我每天给你投资100万元, 连续一个月(30天),但有一个条件:
猴哥,能不能帮帮我……
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
第一天出1元入100万;第二天出2元入100万;第三天出4元入100万元;……哇,发了……
这猴子会不会又在耍我?
……
假如你是高老庄集团企划部的高参,请你帮八戒决策.
情
境
设
置
生
活
化
引
探
升
练
释
延
引
过程分析
营造积极、和谐的学习气氛,使学生产生学习心理倾向,并进一步了解数学来源于生活.
引
探
升
练
释
延
引
情
境
设
置
生
活
化
过程分析
引
探
升
练
释
延
引
探
=
探
究
问
题
活
动
化
领悟
数学
应用
价值
等比数列的前n项和
过程分析
错位相减法
◆学生开展合作学习,讨论交流
一般地,等比数列的前n项和
=
=
即
“请你用错位相减法或者其他方法在这两个式子中
任选一个进行研究.”
引发学生寻求其他方法的内驱力.
引
探
升
练
释
延
探
◆学生自主探究
从特殊到一般,从模仿到创新,有利于学生的知识迁移和能力提高.
探
究
问
题
活
动
化
过程分析
探
究
问
题
活
动
化
引
探
升
练
释
延
探
错位相减法1
错位相减法2
提取公比q
累加法
共享学习成果,体验数学学习成功的喜悦.
……
过程分析
等比数列 ,公比为 ,它的前 项和
即
n为奇数,q为-1时此法不适用
探
究
问
题
活
动
化
引
探
升
练
释
延
探
错位相减法1
错位相减法2
提取公比q
累加法
共享学习成果,体验数学学习成功的喜悦.
……
过程分析
增强思维的严谨性.
引
探
升
练
释
延
探
探
究
问
题
活
动
化
过程分析
剖析公式中的基本量.
进行正反两方面的“短、平、快” 练习.通过总结、辨析和反思,强化公式的结构特征.
辨
析
质
疑
结
构
化
引
探
升
练
释
延
探
释
过程分析
渗透方程思想.通过公式的正用和逆用进一步提高学生运用知识的能力.
引
探
升
练
释
延
释
练
巩
固
提
高
梯
度
化
过程分析
巩
固
提
高
梯
度
化
增加思维的梯度的同时,提高学生的模式识别能力,渗透转化思想.
引
探
升
练
释
延
练
过程分析
让学生进一步认识到数学来源于生活并应用于生活,生活中处处有数学.
引
探
升
练
释
延
练
巩
固
提
高
梯
度
化
过程分析
形成知识模块,从知识的归纳延伸到思想方法的提炼,优化学生的认知结构.
反
思
提
炼
模
块
化
引
探
升
练
释
延
练
升
过程分析
q≠1,q=1
分类讨论
乘公比
错位相减
转
化
思
想
方
程
思
想
数学
源于生活
数学
用于生活
或
知三求二
分组求和
等比数列的
前n项和公式
使各个层次的学生都有所发展. 介绍相关网站,以利于学生开展研究性学习,拓展学生的视野.
作
业
布
置
弹
性
化
引
探
升
练
释
延
升
延
过程分析
弹性化
模块化
梯度化
结构化
活动化
教学目标
————————
重点难点
生活化
升
练
释
探
引
创设情境
探究问题
辨析质疑
巩固提高
反思提炼
延
作业布置
教学说明
新课标人教版课件系列
《高中数学》
必修5
2.5《等比数列的前n项和》
审校:王伟
教学目标
知识与技能:掌握等比数列的前n项和公式,并用公式解决实际问题
过程与方法:由研究等比数列的结构特点推导出等比数列的前n项和公式
情态与价值:从“错位相减法”这种算法中,体会“消除差别”,培养化简的能力
(二)教学重、难点
重点:使学生掌握等比数列的前n项和公式,用等比数列的前n项和公式解决实际问题
难点:由研究等比数列的结构特点推导出等比数列的前n项和公式
教材分析
教学方法
学情分析
教学说明
教学目标
———————
重点难点
教学过程
有助于提升学生的创新思维和探索精神,是培养学生应用意识和数学能力的良好载体.
等比数列的前n项和是“等差数列及其前n项和”与“等比数列”内容的延续、与函数等知识有着密切的联系,又为学习“数列的极限”等内容作准备,具有承上启下的作用.
教材分析
学情分析
认知
情感
能力
掌握等差数列和等比数列的有关知识.
初步具备运用知识解决问题的能力;但对知识的整合能力、问题的探究能力及思维的严密性上还需要进一步培养和提高.
学习兴趣比较浓,表现欲较强,但合作交流的意识等方面尚有待加强.
重点难点
重点:
等比数列的前n项和公式的推导及其简单应用.
知识技能线
情感态度线
过程方法线
观察分析
特殊到一般
灵活运用能力及应用意识
问题情境
公式推导
公式运用
探究尝试
错位相减等
灵活运用
转化、方程思想
突重点
观察能力
合作交流、解决问题能力
抓三线、
重点难点
难点:
等比数列的前n项和公式的推导.
抓两点、破难点
情感、思维的兴奋点
知识选择的切入点
◆学生认知
◆知识特点
教学方法
问题情境
公式推导
公式运用
启发式和探究式相结合的教学方法
计算机、实物投影等辅助教学
教学策略
教学手段
合作探究
自主探究
结构
核心定义
知、情、意、行
教学目标
————————
重点难点
教学过程
升
练
释
探
引
过程分析
创设情境
探究问题
辨析质疑
巩固提高
反思提炼
延
作业布置
引
探
升
练
释
延
引
高老庄集团
高老庄
哈哈,我是CEO了……
情
境
设
置
生
活
化
西游记后传
过程分析
周转不灵……
引
探
升
练
释
延
引
情
境
设
置
生
活
化
西游记后传
过程分析
西游记后传
No problem!我每天给你投资100万元, 连续一个月(30天),但有一个条件:
猴哥,能不能帮帮我……
第一天返还1元,
第二天返还2元,
第三天返还4元……
后一天返还数为前一天的2倍.
第一天出1元入100万;第二天出2元入100万;第三天出4元入100万元;……哇,发了……
这猴子会不会又在耍我?
……
假如你是高老庄集团企划部的高参,请你帮八戒决策.
情
境
设
置
生
活
化
引
探
升
练
释
延
引
过程分析
营造积极、和谐的学习气氛,使学生产生学习心理倾向,并进一步了解数学来源于生活.
引
探
升
练
释
延
引
情
境
设
置
生
活
化
过程分析
引
探
升
练
释
延
引
探
=
探
究
问
题
活
动
化
领悟
数学
应用
价值
等比数列的前n项和
过程分析
错位相减法
◆学生开展合作学习,讨论交流
一般地,等比数列的前n项和
=
=
即
“请你用错位相减法或者其他方法在这两个式子中
任选一个进行研究.”
引发学生寻求其他方法的内驱力.
引
探
升
练
释
延
探
◆学生自主探究
从特殊到一般,从模仿到创新,有利于学生的知识迁移和能力提高.
探
究
问
题
活
动
化
过程分析
探
究
问
题
活
动
化
引
探
升
练
释
延
探
错位相减法1
错位相减法2
提取公比q
累加法
共享学习成果,体验数学学习成功的喜悦.
……
过程分析
等比数列 ,公比为 ,它的前 项和
即
n为奇数,q为-1时此法不适用
探
究
问
题
活
动
化
引
探
升
练
释
延
探
错位相减法1
错位相减法2
提取公比q
累加法
共享学习成果,体验数学学习成功的喜悦.
……
过程分析
增强思维的严谨性.
引
探
升
练
释
延
探
探
究
问
题
活
动
化
过程分析
剖析公式中的基本量.
进行正反两方面的“短、平、快” 练习.通过总结、辨析和反思,强化公式的结构特征.
辨
析
质
疑
结
构
化
引
探
升
练
释
延
探
释
过程分析
渗透方程思想.通过公式的正用和逆用进一步提高学生运用知识的能力.
引
探
升
练
释
延
释
练
巩
固
提
高
梯
度
化
过程分析
巩
固
提
高
梯
度
化
增加思维的梯度的同时,提高学生的模式识别能力,渗透转化思想.
引
探
升
练
释
延
练
过程分析
让学生进一步认识到数学来源于生活并应用于生活,生活中处处有数学.
引
探
升
练
释
延
练
巩
固
提
高
梯
度
化
过程分析
形成知识模块,从知识的归纳延伸到思想方法的提炼,优化学生的认知结构.
反
思
提
炼
模
块
化
引
探
升
练
释
延
练
升
过程分析
q≠1,q=1
分类讨论
乘公比
错位相减
转
化
思
想
方
程
思
想
数学
源于生活
数学
用于生活
或
知三求二
分组求和
等比数列的
前n项和公式
使各个层次的学生都有所发展. 介绍相关网站,以利于学生开展研究性学习,拓展学生的视野.
作
业
布
置
弹
性
化
引
探
升
练
释
延
升
延
过程分析
弹性化
模块化
梯度化
结构化
活动化
教学目标
————————
重点难点
生活化
升
练
释
探
引
创设情境
探究问题
辨析质疑
巩固提高
反思提炼
延
作业布置
教学说明
