数学:2.2.1《等差数列》课件(新人教a版必修5)
文档属性
| 名称 | 数学:2.2.1《等差数列》课件(新人教a版必修5) |  | |
| 格式 | zip | ||
| 文件大小 | 160.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-26 16:05:46 | ||
图片预览








文档简介
(共26张PPT)
新课标人教版课件系列
《高中数学》
必修5
2.2.1《等差数列》
教学目标
1.知识与技能:通过实例,理解等差数列的概念;探索并掌握等差数列的通项公式;能在具体的问题情境中,发现数列的等差关系并能用有关知识解决相应的问题;
2. 过程与方法:让学生对日常生活中实际问题分析,引导学生通过观察,推导,归纳抽象出等差数列的概念;由学生建立等差数列模型用相关知识解决一些简单的问题,进行等差数列通项公式应用的实践操作并在操作过程中
3、掌握"判断数列是否为等差数列"常用的方法;
4、进一步熟练掌握等差数列的通项公式、性质及应用.
5、进一步熟练掌握等差数列的通项公式、性质及应用.
二、教学重、难点
重点:
理解等差数列的概念及其性质,探索并掌握等差数列的通项公式;等差数列的通项公式、性质及应用。
难点:
概括通项公式推导过程中体现出的数学思想方法。灵活应用等差数列的定义及性质解决一些相关问题.
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
主持人问: 最近的时间什么时候可以看到哈雷慧星?
天文学家陈丹说: 2062年左右。
相差76
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。
8844.43米
高度(km)
温度(℃)
1
2
3
28
21.5
15
4
5
8.5
2
…
…
9
-24
(2) 28, 21.5, 15, 8.5, 2, …, -24.
减少6.5
你能根据规律在( )内填上合适的数吗?
(3) 1,4,7,10,( ),16,…
(4) 2, 0, -2, -4, -6,( )…
(1)1682,1758,1834,1910,1986,(2062).
( 2 ) 32, 25.5, 19, 12.5, 6, …, (-20).
13
-8
( 3 ) 1,4,7,10,( 13 ),16,…
( 4 ) 2,0,-2,-4,-6,( -8 ),…
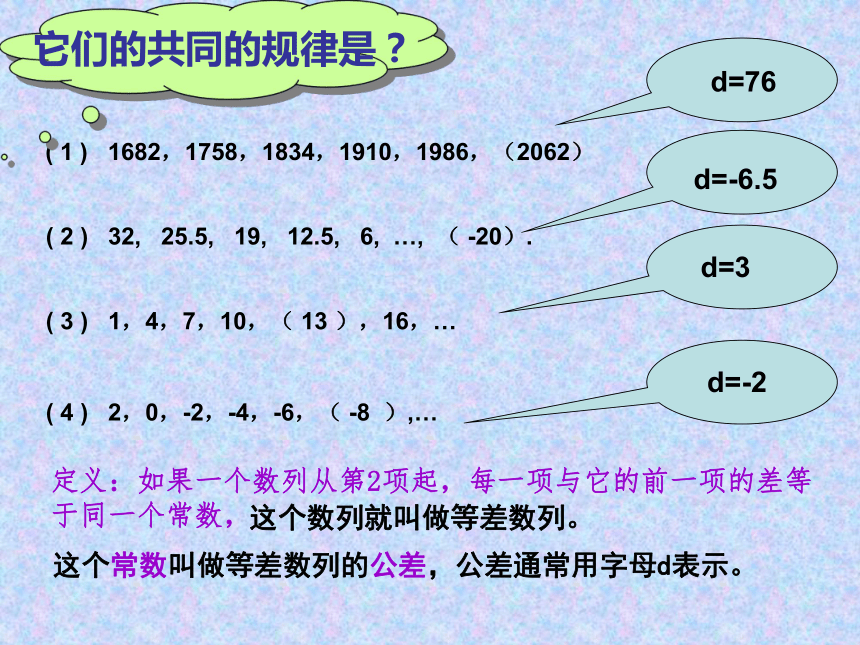
( 1 ) 1682,1758,1834,1910,1986,(2062)
( 2 ) 32, 25.5, 19, 12.5, 6, …, ( -20).
定义:如果一个数列从第2项起,每一项与它的前一项的差等 于同一个常数,
d=76
d=-6.5
d=3
d=-2
这个常数叫做等差数列的公差,公差通常用字母d表示。
这个数列就叫做等差数列。
它们的共同的规律是?
它们是等差数列吗?
(6) 5,5,5,5,5,5,…
公差 d=0 常数列
公差 d= 2x
(5) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
×
(7)
(3) 1,4,7,10,13,16,…
(4) 2,0,-2,-4,-6,-8 …
你会求它们的通项公式吗?
等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…
n=1时亦适合
迭加得
…
等差数列的通项公式
例1 (1) 求等差数列8,5,2,…,的第20项。
解:
(2) 等差数列 -5,-9,-13,…,的第几项是 –401?
解:
因此,
解得
,
20
,
3
8
5
,
8
1
=
-
=
-
=
=
n
d
a
Q
用一下
1. 求等差数列3,7,11,…的第4,7,10项;
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,- ,-7…中的项;
练一练
例2 在等差数列中,已知a5=10,a12=31,
解:由题意可知
这是一个以 和 为未知数的二元一次方程组,解这个方程组,得
即这个等差数列的首项是-2,公差是3.
求首项a1与公差d.
练一练
4. 在等差数列中
小结:
1. 通过本节学习,首先要理解与掌握等差数列的定义
2.要会推导等差数列的通项公式,并掌握其基本应用.
课后作业
课本P45习题2.2[A组]的第1题
定义:如果一个数列从第2项起,每一项与它的前一项的差等 于同一个常数,
这个常数叫做等差数列的公差,公差通常用字母d表示。
这个数列就叫做等差数列。
⑴.公差d一定是由后项减前项所得,而不能用前项减后项来求;
(2)对于数列{ },若 - =d (与n无关的数或字母),n≥2,n∈N,则此数列是等差数列,d 为公差。
等差数列
等差数列的通项公式:
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4 (2)-12,( ) ,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
思 考
( 3 ) , ( ) ,
例3 已知数列 的通项公式为 其中 为常数,那么这个数列一定是等差数列吗 若是,首项与公差分别是什么?
[补充例题]
在等差数列{ }中,若 + =9, ‘ =7, 求 , .
小结:
1. 通过本节学习,首先要理解与掌握等差数列的定义
2.要会推导等差数列的通项公式,并掌握其基本应用.
课后作业
课本P45练习第3题,A组第3题.
300< 83+5×(n-1)500
巩固练习
1.等差数列{an}的前三项依次为 a-6,-3a-5,-10a-1,
则 a 等于( )
A. 1 B. -1 C.- D.
2. 在数列{an}中a1=1,an= an+1+4,则a10= .
(-3a-5 )-(a-6)=(-10a-1) -(-3a-5 )
提示:
提示:
d=an+1- an=-4
3. 在等差数列{an}中a1=83,a4=98,则这个数列有
多少项在300到500之间?
-35
提示:
n=45,46,…,84
40
新课标人教版课件系列
《高中数学》
必修5
2.2.1《等差数列》
教学目标
1.知识与技能:通过实例,理解等差数列的概念;探索并掌握等差数列的通项公式;能在具体的问题情境中,发现数列的等差关系并能用有关知识解决相应的问题;
2. 过程与方法:让学生对日常生活中实际问题分析,引导学生通过观察,推导,归纳抽象出等差数列的概念;由学生建立等差数列模型用相关知识解决一些简单的问题,进行等差数列通项公式应用的实践操作并在操作过程中
3、掌握"判断数列是否为等差数列"常用的方法;
4、进一步熟练掌握等差数列的通项公式、性质及应用.
5、进一步熟练掌握等差数列的通项公式、性质及应用.
二、教学重、难点
重点:
理解等差数列的概念及其性质,探索并掌握等差数列的通项公式;等差数列的通项公式、性质及应用。
难点:
概括通项公式推导过程中体现出的数学思想方法。灵活应用等差数列的定义及性质解决一些相关问题.
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
主持人问: 最近的时间什么时候可以看到哈雷慧星?
天文学家陈丹说: 2062年左右。
相差76
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。
8844.43米
高度(km)
温度(℃)
1
2
3
28
21.5
15
4
5
8.5
2
…
…
9
-24
(2) 28, 21.5, 15, 8.5, 2, …, -24.
减少6.5
你能根据规律在( )内填上合适的数吗?
(3) 1,4,7,10,( ),16,…
(4) 2, 0, -2, -4, -6,( )…
(1)1682,1758,1834,1910,1986,(2062).
( 2 ) 32, 25.5, 19, 12.5, 6, …, (-20).
13
-8
( 3 ) 1,4,7,10,( 13 ),16,…
( 4 ) 2,0,-2,-4,-6,( -8 ),…
( 1 ) 1682,1758,1834,1910,1986,(2062)
( 2 ) 32, 25.5, 19, 12.5, 6, …, ( -20).
定义:如果一个数列从第2项起,每一项与它的前一项的差等 于同一个常数,
d=76
d=-6.5
d=3
d=-2
这个常数叫做等差数列的公差,公差通常用字母d表示。
这个数列就叫做等差数列。
它们的共同的规律是?
它们是等差数列吗?
(6) 5,5,5,5,5,5,…
公差 d=0 常数列
公差 d= 2x
(5) 1, 3, 5, 7, 9, 2, 4, 6, 8, 10
×
(7)
(3) 1,4,7,10,13,16,…
(4) 2,0,-2,-4,-6,-8 …
你会求它们的通项公式吗?
等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…
n=1时亦适合
迭加得
…
等差数列的通项公式
例1 (1) 求等差数列8,5,2,…,的第20项。
解:
(2) 等差数列 -5,-9,-13,…,的第几项是 –401?
解:
因此,
解得
,
20
,
3
8
5
,
8
1
=
-
=
-
=
=
n
d
a
Q
用一下
1. 求等差数列3,7,11,…的第4,7,10项;
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,- ,-7…中的项;
练一练
例2 在等差数列中,已知a5=10,a12=31,
解:由题意可知
这是一个以 和 为未知数的二元一次方程组,解这个方程组,得
即这个等差数列的首项是-2,公差是3.
求首项a1与公差d.
练一练
4. 在等差数列中
小结:
1. 通过本节学习,首先要理解与掌握等差数列的定义
2.要会推导等差数列的通项公式,并掌握其基本应用.
课后作业
课本P45习题2.2[A组]的第1题
定义:如果一个数列从第2项起,每一项与它的前一项的差等 于同一个常数,
这个常数叫做等差数列的公差,公差通常用字母d表示。
这个数列就叫做等差数列。
⑴.公差d一定是由后项减前项所得,而不能用前项减后项来求;
(2)对于数列{ },若 - =d (与n无关的数或字母),n≥2,n∈N,则此数列是等差数列,d 为公差。
等差数列
等差数列的通项公式:
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4 (2)-12,( ) ,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
思 考
( 3 ) , ( ) ,
例3 已知数列 的通项公式为 其中 为常数,那么这个数列一定是等差数列吗 若是,首项与公差分别是什么?
[补充例题]
在等差数列{ }中,若 + =9, ‘ =7, 求 , .
小结:
1. 通过本节学习,首先要理解与掌握等差数列的定义
2.要会推导等差数列的通项公式,并掌握其基本应用.
课后作业
课本P45练习第3题,A组第3题.
300< 83+5×(n-1)500
巩固练习
1.等差数列{an}的前三项依次为 a-6,-3a-5,-10a-1,
则 a 等于( )
A. 1 B. -1 C.- D.
2. 在数列{an}中a1=1,an= an+1+4,则a10= .
(-3a-5 )-(a-6)=(-10a-1) -(-3a-5 )
提示:
提示:
d=an+1- an=-4
3. 在等差数列{an}中a1=83,a4=98,则这个数列有
多少项在300到500之间?
-35
提示:
n=45,46,…,84
40
