二次函数的图像与性质.
图片预览



文档简介
二次函数的图像与性质——
教材分析
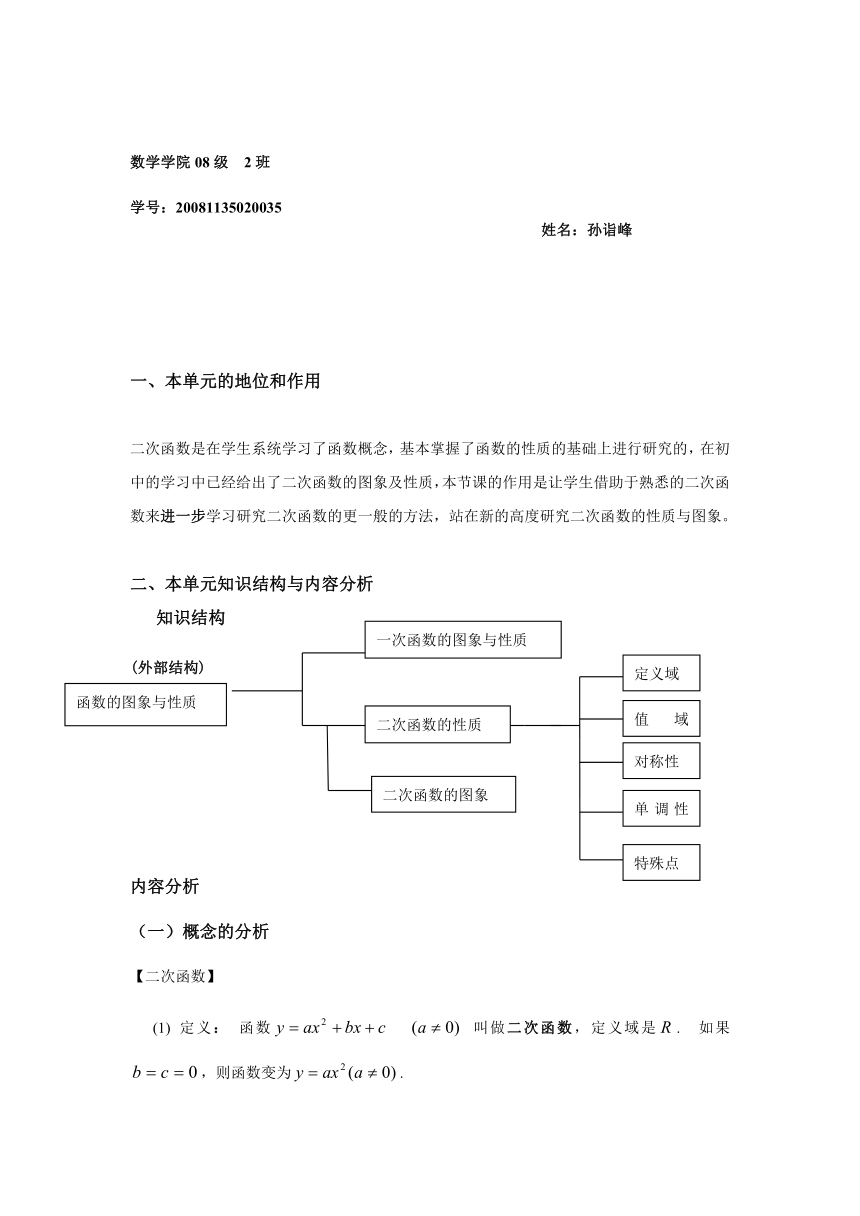
数学学院08级 2班
学号:20081135020035
姓名:孙诣峰
一、本单元的地位和作用
二次函数是在学生系统学习了函数概念,基本掌握了函数的性质的基础上进行研究的,在初中的学习中已经给出了二次函数的图象及性质,本节课的作用是让学生借助于熟悉的二次函数来进一步学习研究二次函数的更一般的方法,站在新的高度研究二次函数的性质与图象。
二、本单元知识结构与内容分析
知识结构
(外部结构)
内容分析
(一)概念的分析
【二次函数】
(1) 定义: 函数 叫做二次函数,定义域是. 如果,则函数变为.
(2)地位与作用:二次函数是本单元的重点内容,是学习二次函数性质与图象的基础,而在高中阶段学习二次函数也为今后学习函数的应用、不等式证明打下基础。
(3)存在性:普遍存在。由于是的特殊形式。
(4)定义方法:属加种差。
(5)关键词:。即二次项系数不能为零,是二次函数的基本条件。
【】与图象的关系
利用学生初中所学的二次函数表达式和其函数图象的关系,通过几个例子引导学生复习记忆。在同一坐标系中,作出
的图象,可以看出,函数中的系数对函数图象的影响。
①时,抛物线开口向上,开口大小随的增大而减小;
②时,抛物线开口向下,开口大小随的增大而增大。
综上总结出抛物线开口大小随的增大而减小。
教材在引入二次函数的一般形式后,主要是通过对具体二次函数的分析,得出二次函数的性质和图象。
【配方法】
配方法的求解过程:
1.转化:将此一元二次方程化为的形式(即一元二次方程的一般形式)
2.系数化1:将二次项系数化为1
3.移项: 将常数项移到等号右侧
4.配方: 等号左右两边同时加上一次项系数一半的平方
5.变形: 将等号左边的代数式写成完全平方形式
6.开方: 左右同时开平方
7.求解: 整理即可得到原方程的根
代数式表示方法:
(二)例题分析
例一:研究二次函数的性质和图象。
1、题目类型:求解(函数顶点、与轴交点、增减区间),证明(图象的对称性),列表作图。
2、研究例题所需掌握的数学水平
(1)通过例题使学生掌握以下五个知识点
①求二次函数顶点
引领学生通过配方将原表达式化成顶点式
得出顶点。
②求二次函数与轴交点
考虑函数图象与轴交点,此时,
将二次函数化为一元二次方程:
解方程,方程的解即为函数与x轴交点,
即
③列表作图,画出图象
-7 -6 -5 -4 -3 -2 -1
-2 0
之后引领学生利用初中学过的描点法均匀选取几个点,划出圆滑曲线作图。
④证明二次函数对称性
利用上表和函数的图象容易看出函数是关于对称的,可观察出二次函数为轴对称图形。
在的两边取两个对称的值:
,
可以证明在这两点函数值相等。
通过此步还可以说成抛物线关于直线对称,
即为二次函数的对称轴。
⑤研究二次函数增减性及增减区间
引导学生通过对图象的观察,发现函数的增减性及区间
函数在区间上是减函数
在区间上是增函数
(2)在掌握以上概念的基础上进一步形成技能
例二:研究二次函数的性质和图象。
对任何二次函数
都可以通过配方化为
通过例一与例二的对比得出:
a>0 a<0
图象
定义域 R
值域
顶点 (,)
与x轴交点
与y轴交点 (0,c)
对称轴
单调性 (-∞,)减函数[,+∞), 增函数 (-∞,),增函数[ , 减函数
(3)在例一例二的基础上达到灵活运用程度、使学生形成能力。
课上让学生练习例三,通过对例三讲解,使学生能够灵活运用本单元知识点。
作业:练习A p1。复习巩固知识点:配方法。
练习A p2。练习B p1,p3。复习巩固知识点:函数的性质与图象。
3、例题的目的。
通过对例题的分析与讲解,使学生更直观的理解二次函数的性质及图象,培养学生由特殊发现一般规律的能力。
(三)数学学习心理分析
通过对学生初中所学二次函数知识的回顾,以及本单元与初中二次函数的联系,使学生在原有知识的基础上获得心理意义,但是一定注意新旧知识的区别,以便对本章加以理解、同化。
三、本单元的教学目标及重点、难点分析
1、知识与技能
(1)掌握研究二次函数的一般方法——配方法。
(2)进一步掌握二次函数的图象的定点坐标,对称轴方程、单调区间和最值得求法。
2、过程与方法
(1)养成观察分析能力、引导学生学会用数形结合的方法研究问题。
(2)养成由特殊事例发现一般规律的归纳能力。
3、情感与态度
(1)通过新旧知识的认识冲突,激发求知欲。
(2)通过合作学习,养成团结协作的思想品质。
4、教学的重点和难点
教学重点:运用配方法研究二次函数的性质
教学难点:二次函数的值域、单调区间
一次函数的图象与性质
函数的图象与性质
定义域
二次函数的性质
值 域
二次函数的图象
对称性
单调性
特殊点
教材分析
数学学院08级 2班
学号:20081135020035
姓名:孙诣峰
一、本单元的地位和作用
二次函数是在学生系统学习了函数概念,基本掌握了函数的性质的基础上进行研究的,在初中的学习中已经给出了二次函数的图象及性质,本节课的作用是让学生借助于熟悉的二次函数来进一步学习研究二次函数的更一般的方法,站在新的高度研究二次函数的性质与图象。
二、本单元知识结构与内容分析
知识结构
(外部结构)
内容分析
(一)概念的分析
【二次函数】
(1) 定义: 函数 叫做二次函数,定义域是. 如果,则函数变为.
(2)地位与作用:二次函数是本单元的重点内容,是学习二次函数性质与图象的基础,而在高中阶段学习二次函数也为今后学习函数的应用、不等式证明打下基础。
(3)存在性:普遍存在。由于是的特殊形式。
(4)定义方法:属加种差。
(5)关键词:。即二次项系数不能为零,是二次函数的基本条件。
【】与图象的关系
利用学生初中所学的二次函数表达式和其函数图象的关系,通过几个例子引导学生复习记忆。在同一坐标系中,作出
的图象,可以看出,函数中的系数对函数图象的影响。
①时,抛物线开口向上,开口大小随的增大而减小;
②时,抛物线开口向下,开口大小随的增大而增大。
综上总结出抛物线开口大小随的增大而减小。
教材在引入二次函数的一般形式后,主要是通过对具体二次函数的分析,得出二次函数的性质和图象。
【配方法】
配方法的求解过程:
1.转化:将此一元二次方程化为的形式(即一元二次方程的一般形式)
2.系数化1:将二次项系数化为1
3.移项: 将常数项移到等号右侧
4.配方: 等号左右两边同时加上一次项系数一半的平方
5.变形: 将等号左边的代数式写成完全平方形式
6.开方: 左右同时开平方
7.求解: 整理即可得到原方程的根
代数式表示方法:
(二)例题分析
例一:研究二次函数的性质和图象。
1、题目类型:求解(函数顶点、与轴交点、增减区间),证明(图象的对称性),列表作图。
2、研究例题所需掌握的数学水平
(1)通过例题使学生掌握以下五个知识点
①求二次函数顶点
引领学生通过配方将原表达式化成顶点式
得出顶点。
②求二次函数与轴交点
考虑函数图象与轴交点,此时,
将二次函数化为一元二次方程:
解方程,方程的解即为函数与x轴交点,
即
③列表作图,画出图象
-7 -6 -5 -4 -3 -2 -1
-2 0
之后引领学生利用初中学过的描点法均匀选取几个点,划出圆滑曲线作图。
④证明二次函数对称性
利用上表和函数的图象容易看出函数是关于对称的,可观察出二次函数为轴对称图形。
在的两边取两个对称的值:
,
可以证明在这两点函数值相等。
通过此步还可以说成抛物线关于直线对称,
即为二次函数的对称轴。
⑤研究二次函数增减性及增减区间
引导学生通过对图象的观察,发现函数的增减性及区间
函数在区间上是减函数
在区间上是增函数
(2)在掌握以上概念的基础上进一步形成技能
例二:研究二次函数的性质和图象。
对任何二次函数
都可以通过配方化为
通过例一与例二的对比得出:
a>0 a<0
图象
定义域 R
值域
顶点 (,)
与x轴交点
与y轴交点 (0,c)
对称轴
单调性 (-∞,)减函数[,+∞), 增函数 (-∞,),增函数[ , 减函数
(3)在例一例二的基础上达到灵活运用程度、使学生形成能力。
课上让学生练习例三,通过对例三讲解,使学生能够灵活运用本单元知识点。
作业:练习A p1。复习巩固知识点:配方法。
练习A p2。练习B p1,p3。复习巩固知识点:函数的性质与图象。
3、例题的目的。
通过对例题的分析与讲解,使学生更直观的理解二次函数的性质及图象,培养学生由特殊发现一般规律的能力。
(三)数学学习心理分析
通过对学生初中所学二次函数知识的回顾,以及本单元与初中二次函数的联系,使学生在原有知识的基础上获得心理意义,但是一定注意新旧知识的区别,以便对本章加以理解、同化。
三、本单元的教学目标及重点、难点分析
1、知识与技能
(1)掌握研究二次函数的一般方法——配方法。
(2)进一步掌握二次函数的图象的定点坐标,对称轴方程、单调区间和最值得求法。
2、过程与方法
(1)养成观察分析能力、引导学生学会用数形结合的方法研究问题。
(2)养成由特殊事例发现一般规律的归纳能力。
3、情感与态度
(1)通过新旧知识的认识冲突,激发求知欲。
(2)通过合作学习,养成团结协作的思想品质。
4、教学的重点和难点
教学重点:运用配方法研究二次函数的性质
教学难点:二次函数的值域、单调区间
一次函数的图象与性质
函数的图象与性质
定义域
二次函数的性质
值 域
二次函数的图象
对称性
单调性
特殊点
