15.2多边形(一)

崇文中学导学案 15.2多边形(一)
年级：七年级 科目：数学 主备人：宋宏伟 审核人：于建红
教学目标
1、理解多边形的有关概念；
2、探索任意多边形的内角和，体验归纳发现规律的思想方法；
及简单应用；
3、体验把多边形问题转化为三角形问题来解决的化归思想。
4、掌握正多边形的概念及性质
一、知识回顾
1、三角形的有关概念：三角形、边、顶点、角
2、三角形的内角和是______
由这图形你抽象出什么几何图形？
二、探究与发现
探究一看课本153页并填空
1、平面内，不在___________的几条线段________________，所得的图形叫多边形。组成多边形的__________叫多边形的边、相邻两边的__________叫多边形的顶点、相邻两边所_________的角叫多边形内角。简称多边形的角
2、多边形的对角线：连结多边形_______________的线段叫做多边形的对角线。
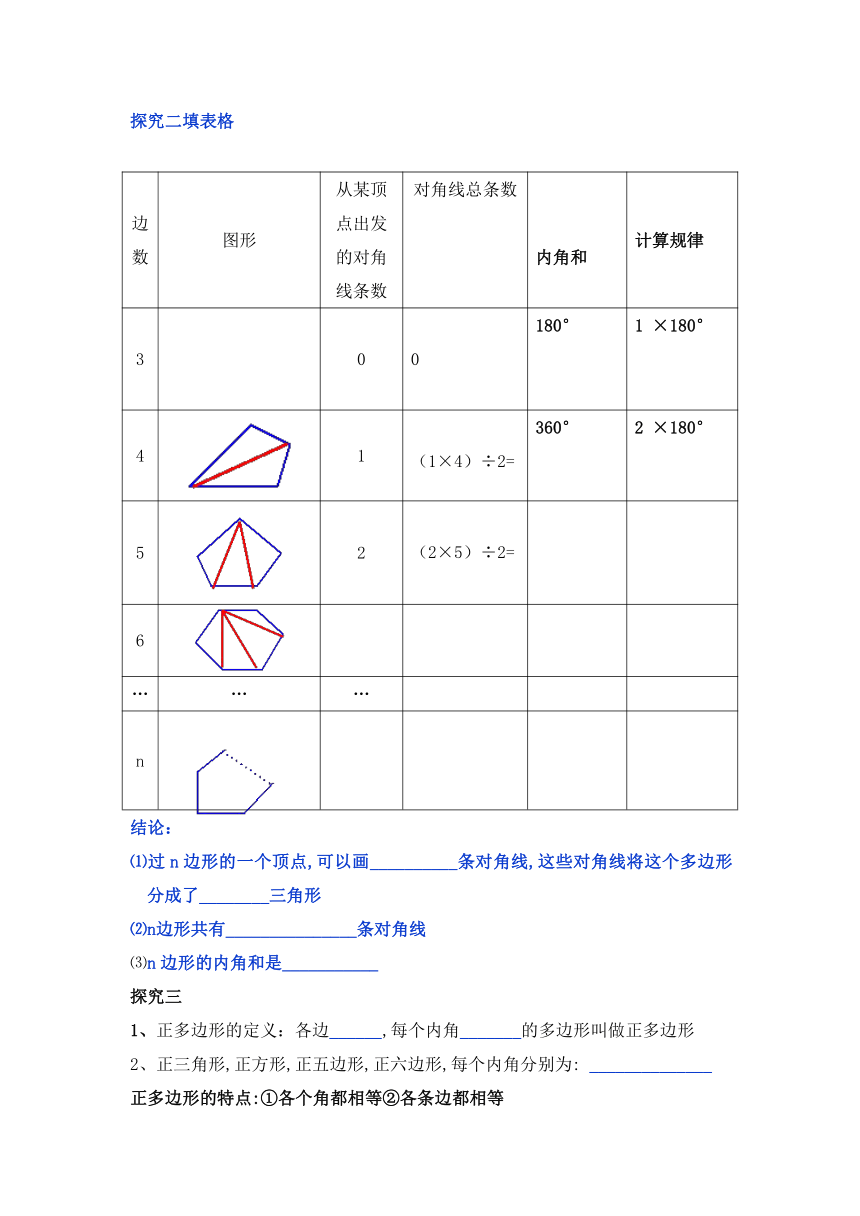
探究二填表格
边数 图形 从某顶点出发的对角线条数 对角线总条数 内角和 计算规律
3 0 0 180° 1 ×180°
4 1 （1×4）÷2= 360° 2 ×180°
5 2 （2×5）÷2=
6
… … …
n
结论：
⑴过n边形的一个顶点,可以画__________条对角线,这些对角线将这个多边形分成了________三角形
⑵n边形共有_______________条对角线
⑶n边形的内角和是___________
探究三
1、正多边形的定义：各边______,每个内角_______的多边形叫做正多边形
2、正三角形,正方形,正五边形,正六边形,每个内角分别为: ______________
正多边形的特点:①各个角都相等②各条边都相等
三、例题
1、一个多边形有14条对角线,求它的内角和与边数
2、一个多边形的每个内角都相等,且一个内角等于它相邻外角的9倍.求这个多边形的边数.
试一试
1.九边形的内角和________
2.一个多边形的内角和为540°,则它是______边形
3.正六边形的每一个内角等于_________
4、从十五边形的一个顶点出发引对角线,把十五边形分成__________三角形
5、一个多边形当边数增加1时，它的内角和增加（ ）。
四、拓展练习
1、2008年北京奥运会马上就要到来了,七年级的学生圆圆有一个设想,她计划设计一个内角和是2008°的多边形图案,这是非常有意义的,圆圆的想法能实现吗 为什么
2、找出四边形内角和的其他论证方法