苏科版九年级下册数学:圆中的相似专题课件(共19张PPT)
文档属性
| 名称 | 苏科版九年级下册数学:圆中的相似专题课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-01 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
圆中的相似专题
课前热身
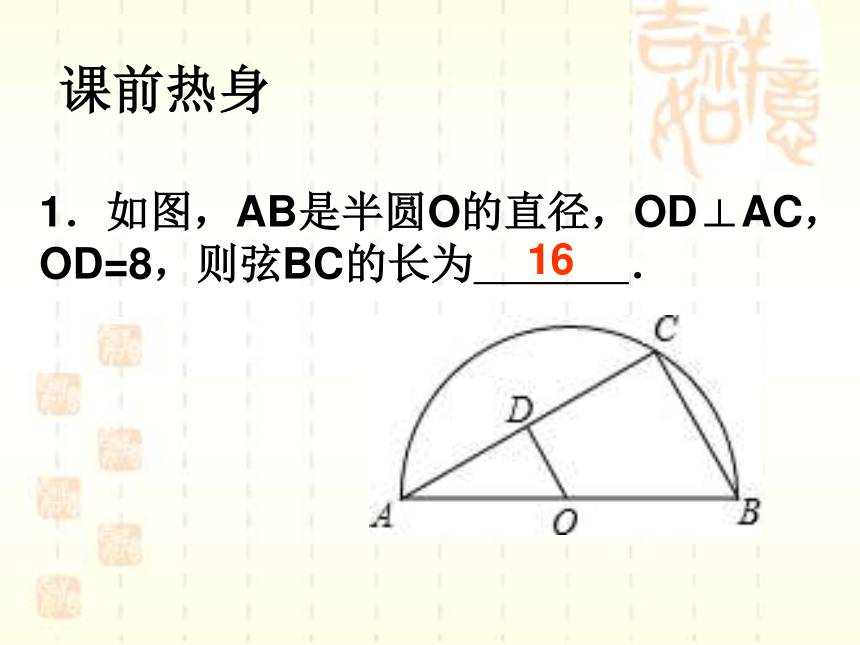
1.如图,AB是半圆O的直径,OD⊥AC,OD=8,则弦BC的长为
.
16
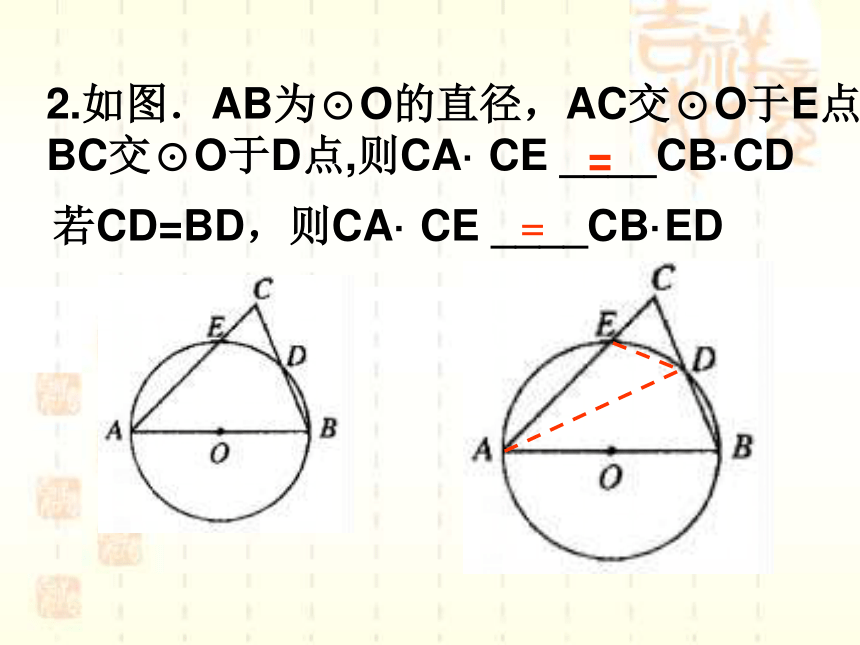
2.如图.AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,则CA·
CE
____CB·CD
=
若CD=BD,则CA·
CE
____CB·ED
=
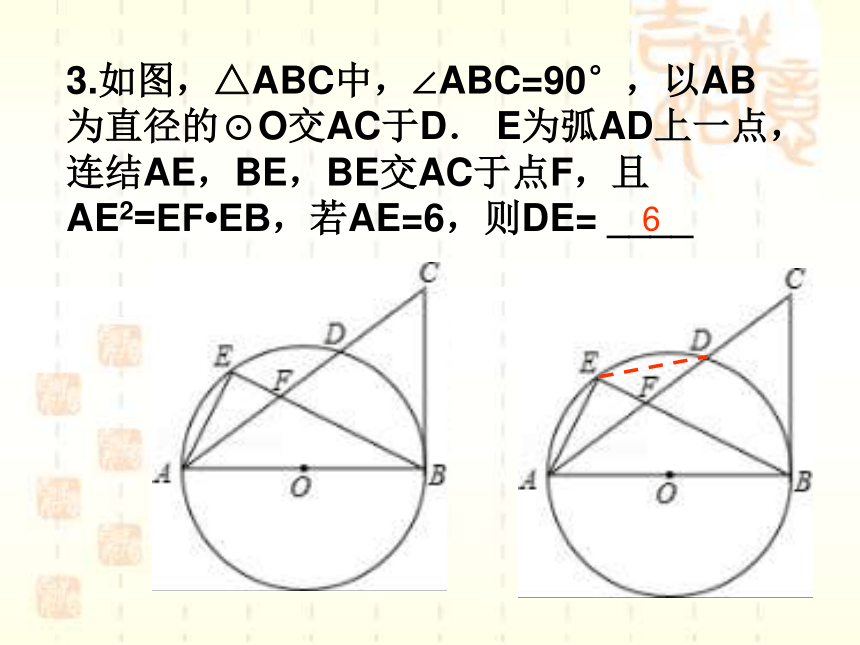
3.如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D.
E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF?EB,若AE=6,则DE=
____
6
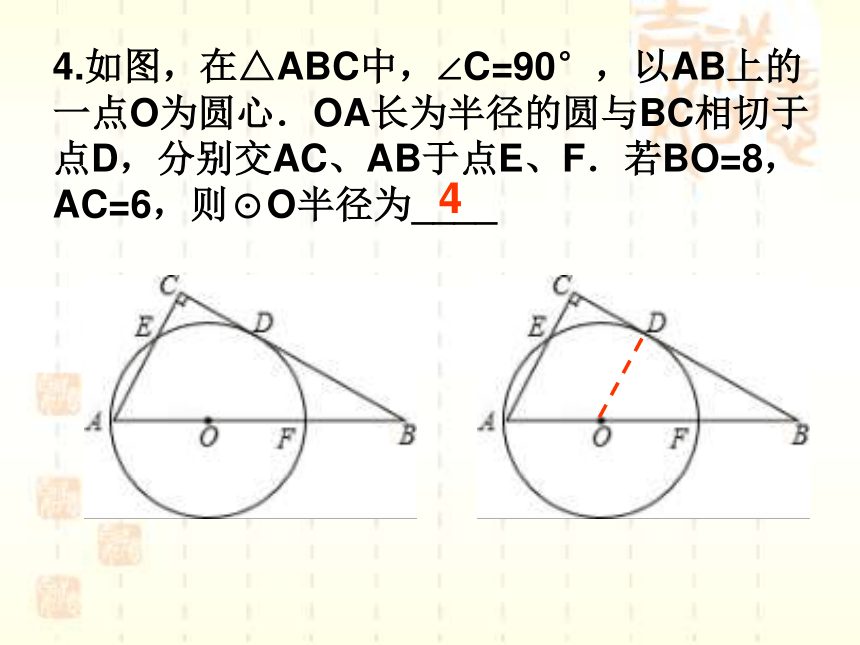
4.如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.若BO=8,AC=6,则⊙O半径为____
4
典型例题
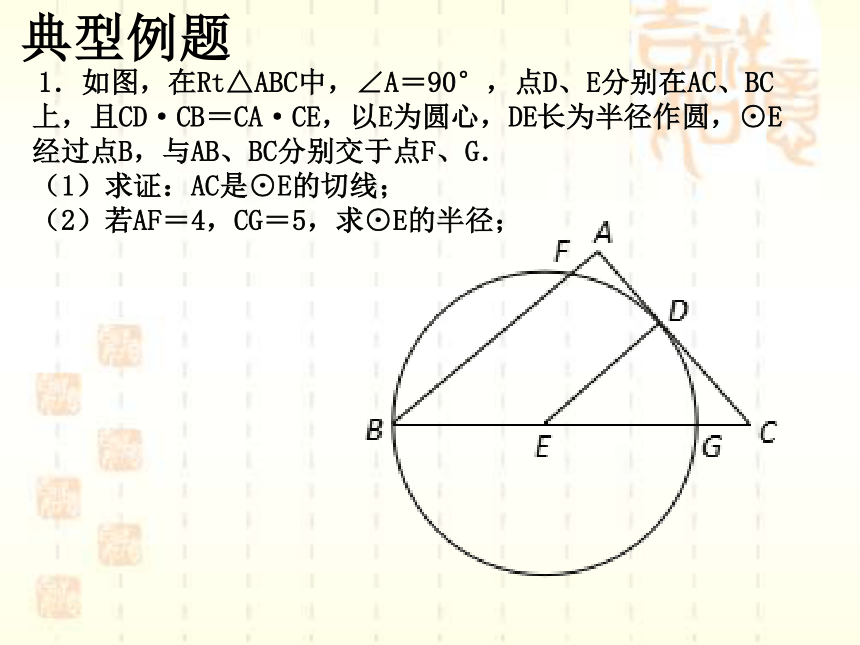
1.如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD·CB=CA·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,求⊙E的半径;
证明:
(1)∵CD?BC=AC?CE,
∴
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线;
(2)如图,过E作EH⊥AB于H,
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH﹣AF=DE﹣AF=r﹣4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴
,即
,
∴r=20,
∴⊙E的半径为20;
2.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:∠ODF=∠BDE;
(2)求证:△DOE∽△ABC;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若
,求
的值.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是
所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC;
(3)解:∵
,
∴设OE=2a,OD=3a,
∴OB=OC=OD=3a,AB=2OD=6a,
∵△DOE~△ABC,
∴
=(
)2
=
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOC=
S△ABC,
即S△BOC=2S1,
∵DE⊥AB,
∴∠BED=90°,
∵BE=OB﹣OE=3a﹣2a=a,
∴S△DBE=
BE×DE=
a×DE=
×
×2a×DE=
×
×DE=
S1,
∵S2=S△BOC+S△DOE+S△DBE=2S1+S1+
S1=
S1,
∴
=
=
3.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)设DE交AB于点G,若DF=4,cosB=
,E是
的中点,求EG?ED的值.
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=
,BD=4,
∴AB=6,
∵E是
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3
,
∵E是
的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴
=
,即EG?ED=AE2=18.
小试牛刀
1.如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:AB?CD=AE?AC.
(3)若BD=2CD,设△EBD的面积为
,△ADC的面积为
,且
,求△ABC的面积.
2.如图,AB是⊙O的直径,点C是的弧AB中点,点D是⊙
外一点,AD=AB
,
AD交⊙O于F,BD交⊙O于E
,连接CE交AB
于G
.
(1)证明:
;
(2)若
,求
的度数;
(3)若
,求
的值.
3.如图,A
是以
BC为直径的⊙O
上一点,AD⊥BC
于点
D,过点B
作
⊙O的切线,与CA
的延长线相交于点E,G
是AD
的中点,连结CG
并延长与BE
相交于点F
,延长AF
与CA
的延长线相交于点P
.
(1)求证:BE=EF
;
(2)求证:PA
是⊙O
的切线;
(3)若FG=BF
,且⊙O
的半径长为
,求BD
和
FG的长度.
课堂小结
圆中的相似专题
课前热身
1.如图,AB是半圆O的直径,OD⊥AC,OD=8,则弦BC的长为
.
16
2.如图.AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,则CA·
CE
____CB·CD
=
若CD=BD,则CA·
CE
____CB·ED
=
3.如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D.
E为弧AD上一点,连结AE,BE,BE交AC于点F,且AE2=EF?EB,若AE=6,则DE=
____
6
4.如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.若BO=8,AC=6,则⊙O半径为____
4
典型例题
1.如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD·CB=CA·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,求⊙E的半径;
证明:
(1)∵CD?BC=AC?CE,
∴
,
∵∠DCE=∠ACB,
∴△CDE∽△CAB,
∴∠EDC=∠A=90°,
∴ED⊥AC,
∵点D在⊙E上,
∴AC是⊙E的切线;
(2)如图,过E作EH⊥AB于H,
∴BH=FH,
∵∠A=∠AHE=∠ADE=90°,
∴四边形AHED是矩形,
∴ED=AH,ED∥AB,
∴∠B=∠DEC,
设⊙E的半径为r,则EB=ED=EG=r,
∴BH=FH=AH﹣AF=DE﹣AF=r﹣4,
EC=EG+CG=r+5,
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC=90°,
∴△BHE∽△EDC,
∴
,即
,
∴r=20,
∴⊙E的半径为20;
2.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:∠ODF=∠BDE;
(2)求证:△DOE∽△ABC;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若
,求
的值.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是
所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC;
(3)解:∵
,
∴设OE=2a,OD=3a,
∴OB=OC=OD=3a,AB=2OD=6a,
∵△DOE~△ABC,
∴
=(
)2
=
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOC=
S△ABC,
即S△BOC=2S1,
∵DE⊥AB,
∴∠BED=90°,
∵BE=OB﹣OE=3a﹣2a=a,
∴S△DBE=
BE×DE=
a×DE=
×
×2a×DE=
×
×DE=
S1,
∵S2=S△BOC+S△DOE+S△DBE=2S1+S1+
S1=
S1,
∴
=
=
3.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)设DE交AB于点G,若DF=4,cosB=
,E是
的中点,求EG?ED的值.
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=
,BD=4,
∴AB=6,
∵E是
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3
,
∵E是
的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴
=
,即EG?ED=AE2=18.
小试牛刀
1.如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:AB?CD=AE?AC.
(3)若BD=2CD,设△EBD的面积为
,△ADC的面积为
,且
,求△ABC的面积.
2.如图,AB是⊙O的直径,点C是的弧AB中点,点D是⊙
外一点,AD=AB
,
AD交⊙O于F,BD交⊙O于E
,连接CE交AB
于G
.
(1)证明:
;
(2)若
,求
的度数;
(3)若
,求
的值.
3.如图,A
是以
BC为直径的⊙O
上一点,AD⊥BC
于点
D,过点B
作
⊙O的切线,与CA
的延长线相交于点E,G
是AD
的中点,连结CG
并延长与BE
相交于点F
,延长AF
与CA
的延长线相交于点P
.
(1)求证:BE=EF
;
(2)求证:PA
是⊙O
的切线;
(3)若FG=BF
,且⊙O
的半径长为
,求BD
和
FG的长度.
课堂小结
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
