冀教版九年级下册数学第29章 直线与圆的位置关系-圆中的分类讨论 课件 (共16张PPT)
文档属性
| 名称 | 冀教版九年级下册数学第29章 直线与圆的位置关系-圆中的分类讨论 课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 10:17:12 | ||
图片预览


文档简介
(共16张PPT)
圆中的分类讨论
让我们以百倍的信心
驶向成功的彼岸!!!
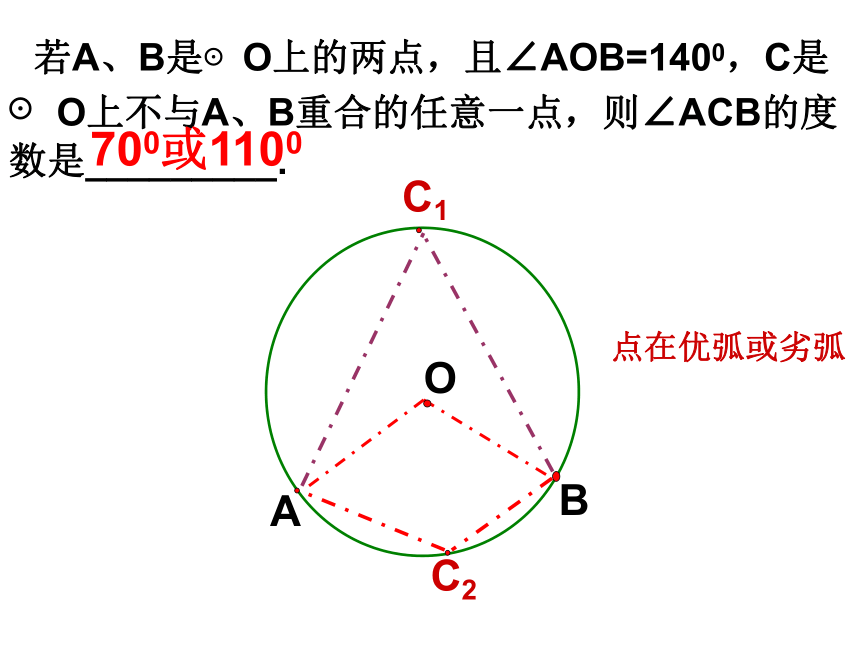
点在优弧或劣弧
若A、B是⊙O上的两点,且∠AOB=1400,C是⊙O上不与A、B重合的任意一点,则∠ACB的度数是_________.
O
B
A
700或1100
分类讨论:
根据某一标准将数学对象分为不同种类,然后分别对它们进行讨论,得出各种情况下相应结论的数学思想方法。
分类讨论是一种重要的数学思想方法也是一种解题的策略!
在几何图形中,我们常根据位置关系不确定进行分类。
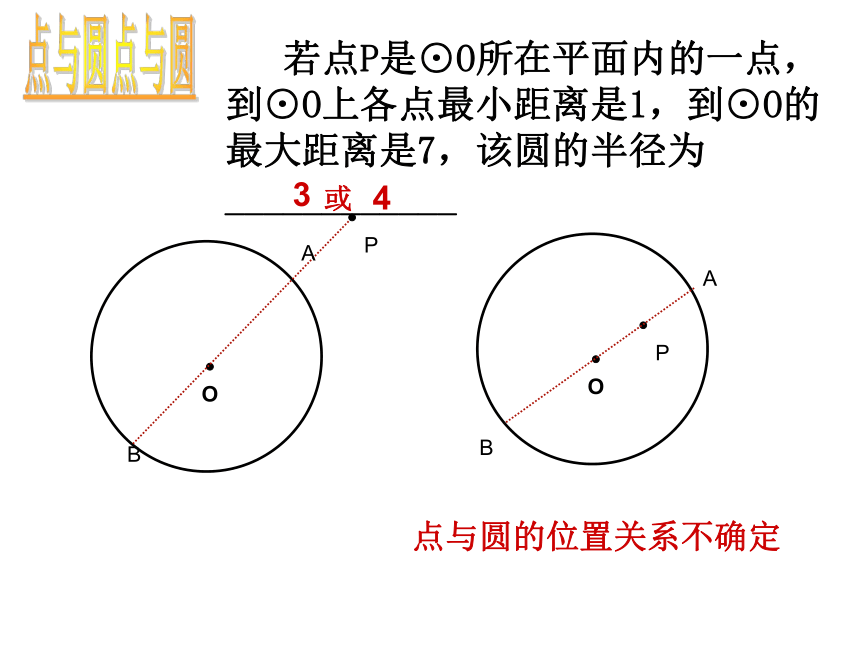
若点P是⊙O所在平面内的一点,到⊙O上各点最小距离是1,到⊙O的最大距离是7,该圆的半径为____________
3
点与圆的位置关系不确定
点与圆
4
或
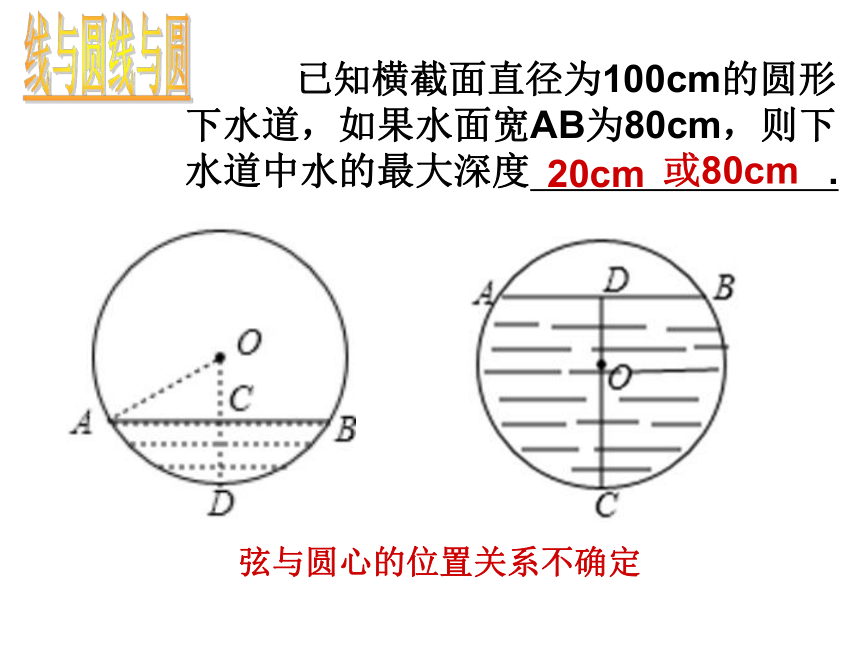
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,则下水道中水的最大深度
.
弦与圆心的位置关系不确定
20cm
或80cm
线与圆
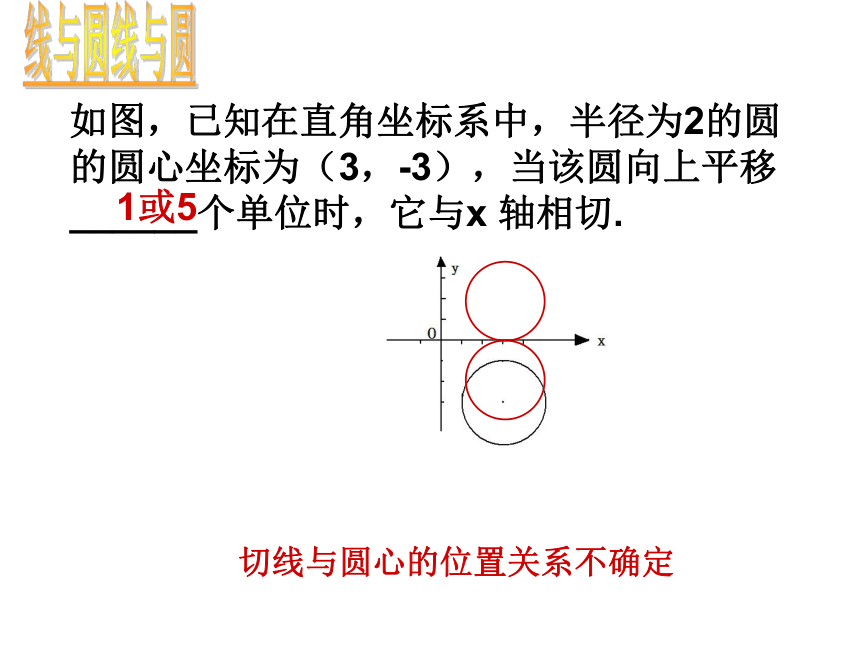
如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),当该圆向上平移______个单位时,它与x
轴相切.
?
?
?
1或5
线与圆
切线与圆心的位置关系不确定
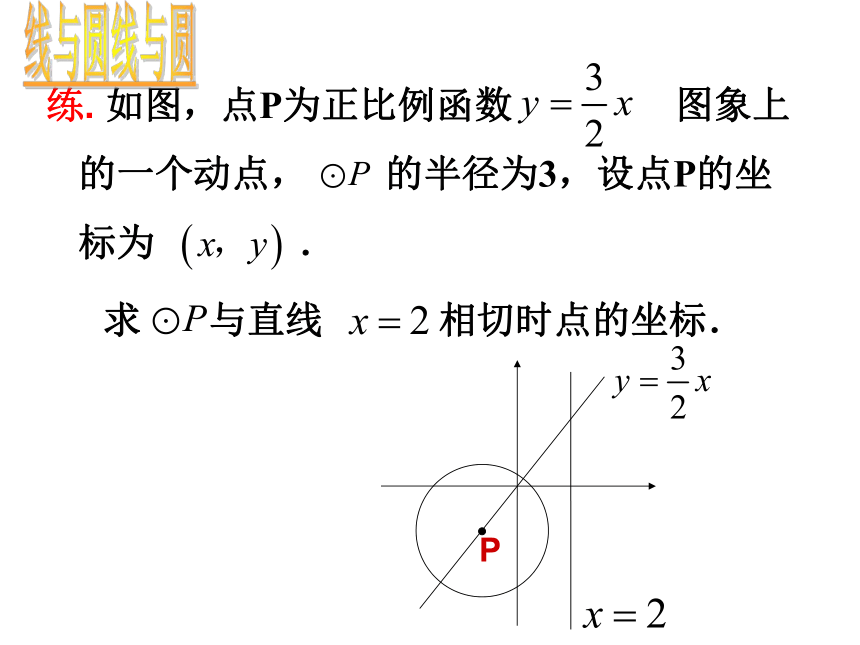
练.
如图,点P为正比例函数
图象上的一个动点,
的半径为3,设点P的坐标为
.
求
与直线
相切时点的坐标.
线与圆
P
x
y
4
-3
7、直线
(1)求M,N两点的坐标;
(2)如果点P在x轴上,以点P为圆心,3为半径
的圆与直线
相切,求点P的坐标.
与x轴,y轴分别交于点M,N
0
M
N
P1
A
P2
B
归纳小结
点、弦、直线与圆位置不确定需分类讨论
圆是轴对称图形
分类思想在动态问题中运用
已知:△ABC是直径为10厘米的⊙O的内接等腰三角形,且底边BC=8厘米,求△ABC的面积;
点与圆
已知⊙O的半径为5cm,AB、CD是⊙O的弦,且AB=6cm,
CD=8cm,AB∥CD,则AB与CD之间的距离为
;
1cm
线与圆
7cm
或
通过本节课的学习你有哪些收获?
与圆有关的分类讨论,常根据位置关系不确定进行分类:
1、点与圆的位置关系不确定
2、点在圆上位置不确定
3、两弦与圆心的位置关系不确定
变式:已知:⊙O半径为1,
AB、
AC
⊙O是弦,AB=
,AC=
,∠BAC的度数为______
两弦与圆心的位置关系不确定
或
线与圆
解:①当P1点在x轴上,并且在M点的左侧时,
设⊙P1与直线
上切于点A,连P1A.
则P1A⊥MN,
∵OA=P1A=3,
∴
∴P1M=MN=5,∴OP1=1.
∴P1点坐标是(-1,0);
②当P2点在x轴上,并且在M点的右侧时,
设⊙P2与直线
上切于点B,连P2B.
则P2B⊥MN,
∵OA=P2B=3,
∴
∴P2M=MN=5,∴OP2=9.
∴P1点坐标是(9,0);
2、弦AB把⊙O的圆周分成1:2,则弦AB
所对的圆周角的度数是
。
点在圆上位置不确定
点与圆
O
Q
再见!
谢谢!
圆中的分类讨论
让我们以百倍的信心
驶向成功的彼岸!!!
点在优弧或劣弧
若A、B是⊙O上的两点,且∠AOB=1400,C是⊙O上不与A、B重合的任意一点,则∠ACB的度数是_________.
O
B
A
700或1100
分类讨论:
根据某一标准将数学对象分为不同种类,然后分别对它们进行讨论,得出各种情况下相应结论的数学思想方法。
分类讨论是一种重要的数学思想方法也是一种解题的策略!
在几何图形中,我们常根据位置关系不确定进行分类。
若点P是⊙O所在平面内的一点,到⊙O上各点最小距离是1,到⊙O的最大距离是7,该圆的半径为____________
3
点与圆的位置关系不确定
点与圆
4
或
已知横截面直径为100cm的圆形下水道,如果水面宽AB为80cm,则下水道中水的最大深度
.
弦与圆心的位置关系不确定
20cm
或80cm
线与圆
如图,已知在直角坐标系中,半径为2的圆的圆心坐标为(3,-3),当该圆向上平移______个单位时,它与x
轴相切.
?
?
?
1或5
线与圆
切线与圆心的位置关系不确定
练.
如图,点P为正比例函数
图象上的一个动点,
的半径为3,设点P的坐标为
.
求
与直线
相切时点的坐标.
线与圆
P
x
y
4
-3
7、直线
(1)求M,N两点的坐标;
(2)如果点P在x轴上,以点P为圆心,3为半径
的圆与直线
相切,求点P的坐标.
与x轴,y轴分别交于点M,N
0
M
N
P1
A
P2
B
归纳小结
点、弦、直线与圆位置不确定需分类讨论
圆是轴对称图形
分类思想在动态问题中运用
已知:△ABC是直径为10厘米的⊙O的内接等腰三角形,且底边BC=8厘米,求△ABC的面积;
点与圆
已知⊙O的半径为5cm,AB、CD是⊙O的弦,且AB=6cm,
CD=8cm,AB∥CD,则AB与CD之间的距离为
;
1cm
线与圆
7cm
或
通过本节课的学习你有哪些收获?
与圆有关的分类讨论,常根据位置关系不确定进行分类:
1、点与圆的位置关系不确定
2、点在圆上位置不确定
3、两弦与圆心的位置关系不确定
变式:已知:⊙O半径为1,
AB、
AC
⊙O是弦,AB=
,AC=
,∠BAC的度数为______
两弦与圆心的位置关系不确定
或
线与圆
解:①当P1点在x轴上,并且在M点的左侧时,
设⊙P1与直线
上切于点A,连P1A.
则P1A⊥MN,
∵OA=P1A=3,
∴
∴P1M=MN=5,∴OP1=1.
∴P1点坐标是(-1,0);
②当P2点在x轴上,并且在M点的右侧时,
设⊙P2与直线
上切于点B,连P2B.
则P2B⊥MN,
∵OA=P2B=3,
∴
∴P2M=MN=5,∴OP2=9.
∴P1点坐标是(9,0);
2、弦AB把⊙O的圆周分成1:2,则弦AB
所对的圆周角的度数是
。
点在圆上位置不确定
点与圆
O
Q
再见!
谢谢!
