苏科版九下数学 7.1正切 教案

7.1　正切
教学目标
1．认识锐角的正切的概念；2．经历操作、观察、思考、求解等过程，感受数形结合的数学思想方法，培养学生理性思维的习惯，提高学生运用数学知识解决实际问题的能力；3．激发学生学习的积极性和主动性，引导学生自主探索、合作交流，培养学生的创新意识．
教学重点
计算一个锐角的正切值的方法．
教学难点
计算一个锐角的正切值的方法．
教学过程（教师）
学生活动
设计思路
新课引入——情景导入问题1：如图1，哪个台阶更陡？
大多数学生会根据自己的生活经验来判断第二个台阶更陡一些，学生的回答大多是建立在倾斜的程度（实际上就是倾斜的角度）．
较好地发挥了“情景导入”的作用，让学生初步体会倾斜的程度可以靠倾斜的角度来判断和辨别，初步感受倾斜的角度越大，台阶就越陡．
思考：除了用∠A的大小来描述倾斜程度，还可以用什么方法？
学生积极思考。
通过设计这个问题激发学生探求知识的欲望，提高学生学习的积极性和主动性。
自主学习：自学课本第96-97页内容，回答以下问题：1.什么叫做∠A的正切？用什么符号表示？2.如何求∠A的正切?
学生自学，小组讨论不懂的知识点。
培养学生自学的能力，提高学生自主探求知识的能力。
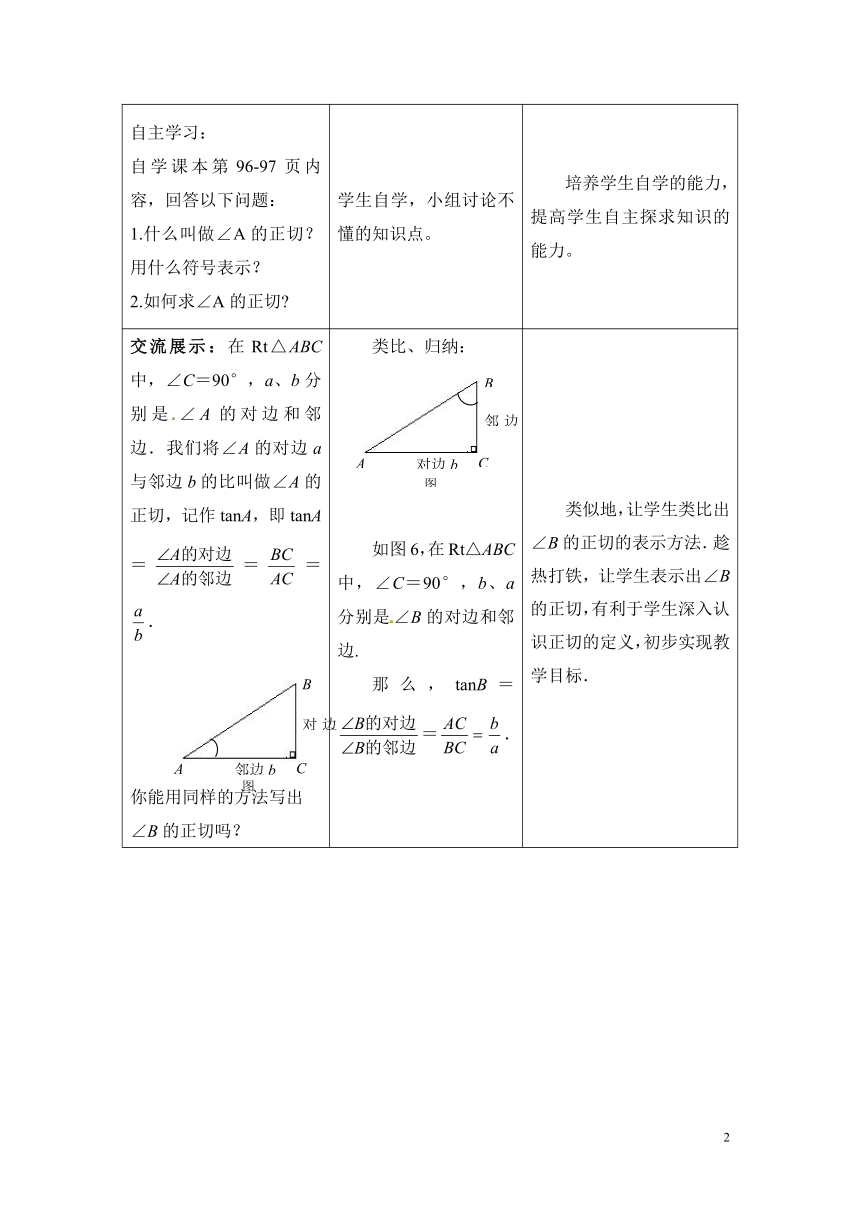
交流展示：在Rt△ABC中，∠C＝90°，a、b分别是∠A的对边和邻边．我们将∠A的对边a与邻边b的比叫做∠A的正切，记作tanA，即tanA＝＝＝．你能用同样的方法写出∠B的正切吗？
类比、归纳：如图6，在Rt△ABC中，∠C＝90°，b、a分别是∠B的对边和邻边.那么，tanB＝＝．
类似地，让学生类比出∠B的正切的表示方法．趁热打铁，让学生表示出∠B的正切，有利于学生深入认识正切的定义，初步实现教学目标．
如图,根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。例1如图7，在Rt△ABC中，∠C＝90°，AC＝4，AB＝5，求tanA、tanB．拓展：通过计算tanA、tanB的值，你有什么新的发现吗？
1.发表意见，表达观点，相互补充．参考答案：例1解：在Rt△ABC中，BC＝，tanA＝，tanB＝．从而发现tanA与tanB互为倒数，即tanA·tanB＝1．而且，根据定义，我们发现tanA·tanB＝·＝1，所以，我们能得到互余两个角的正切值互为倒数．
师生互动，锻炼学生的口头表达能力，培养学生勇于发表自己看法的能力，会进行简单的说理．在拓展环节，尽量让学生表达，或是在互相交流的基础上发表自己的看法，这样有利于学生对知识的进一步理解．
拓展延伸：　例2如图8，在等边三角形ABC中，CD⊥AB，垂足为D．求tanA．
发表意见，表达观点，相互补充．参考答案：解：由题意知，AD＝．
在Rt△ACD中，根据勾股定理，得CD＝＝，tanA＝．
例2主要是针对角不在直角三角形中如何处理，要让学生明白寻找对边或邻边时要在该角所在的直角三角形中实现，从而引导学生去创造直角三角形培养学生分析问题的能力．适时的问题拓展，开放性的问题设计，既综合整理、当堂复习了新课知识要点，又留给了学生自由发挥的空间．
畅所欲言通过这节课的学习，我的收获是…
学生小结
通过小结使学生进一步巩固本节课的知识。
检测反馈1．如图9，求下列图中各直角三角形中锐角的正切值．
运用本节课所学数学知识解决问题．参考答案：1．解：①在Rt△ABC中，tan
A＝，tanB＝．②在Rt△ABC中，AC＝，tanA＝，tanB＝．③在Rt△ABC中，AC＝，tanA＝，tanB＝．
检测学生对本节课知识的掌握程度，考查了学生解决问题的综合能力．练习1让学生体会不同位置摆放的直角三角形不会影响锐角的正切值．其中的第三个图形的设计让第三边AC的结果不是整数（为）．
1
B
C
A
③
B
A
7
5
C
②
C
A
17
15
B
①
C
B
12
A
5
2
图8
5
B
C
4
A
图7
图6
B
邻边a
C
对边b
A
图5
B
对边a
C
邻边b
A
PAGE
5