平行线的判定(三)
图片预览

文档简介
凤阳博文国际学校七年级(下)数学导学案
学科负责人签字:叶 飞 课改中心评价人___________ 得分(等级)_________
课 题:平行线的判定(三) 课型:预习+展示
主备人:叶 飞 备课时间:2011年 5 月 25 日
授课老师: 使用时间:
学习目标:1、在掌握平行线判定方法1的基础上,探讨利用内错角和同旁内角来判定两直线平行.
2.通过平行线判定2和判定3的推理过程进一步学会“说理”,以及理解蕴含其中的化归思想——把新问题转化为已经解决的问题;同时培养数学概括的能力.
学习重点:在掌握平行线的判定方法1的基础上,探讨利用内错角和同旁内角
来判定两直线平行.
学习难点:利用内错角和同旁内角来判定两直线平行.
学生学习过程:(课型不同,学习过程有所不同)
一、旧知回顾
平行线的判定方法1_________________________________________________
二,新知探究
1.如图:直线a、b被直线c所截,如果内错角∠2=∠4相等,那么直线a,b有怎样的位置关系?为什么?
a∥b
说明:∵直线a、b被直线c所截
∴∠1 = ∠2( )
∵∠2 = ∠4( )
∴∠_____ = ∠_____( )
∴a∥b ( )
由此,可得平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:______________________________________
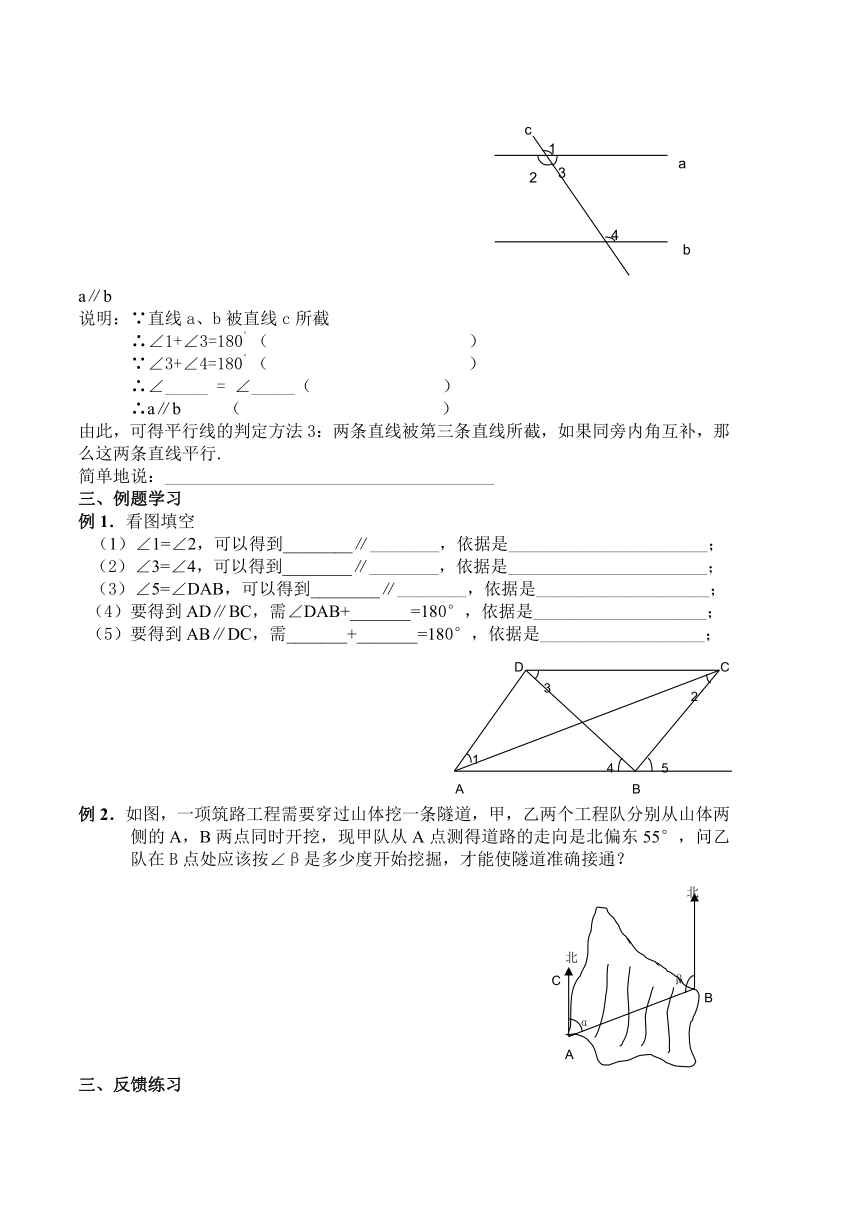
2.如图:直线a、b被直线c所截,如果同旁内角∠3+∠4=180°,那么直线a,b有怎样的位置关系?为什么?
a∥b
说明:∵直线a、b被直线c所截
∴∠1+∠3=180°( )
∵∠3+∠4=180°( )
∴∠_____ = ∠_____( )
∴a∥b ( )
由此,可得平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说:______________________________________
三、例题学习
例1.看图填空
(1)∠1=∠2,可以得到________∥________,依据是_______________________;
(2)∠3=∠4,可以得到________∥________,依据是_______________________;
(3)∠5=∠DAB,可以得到________∥________,依据是____________________;
(4)要得到AD∥BC,需∠DAB+_______=180°,依据是____________________;
(5)要得到AB∥DC,需_______+_______=180°,依据是___________________;
例2.如图,一项筑路工程需要穿过山体挖一条隧道,甲,乙两个工程队分别从山体两侧的A,B两点同时开挖,现甲队从A点测得道路的走向是北偏东55°,问乙队在B点处应该按∠β是多少度开始挖掘,才能使隧道准确接通?
三、反馈练习
1.如图,已知∠1=50°,要使AB∥CD,则须具备另一个条件不成立的是( )
A ∠2=130° B ∠3=50° C ∠4=49° D ∠4=50°
2.如图,已知E、B、C三点共线,BE平分∠DBF,∠1=∠C,可以推出BF∥AC,推理过程如下:
∵BE平分∠DBF ( )
∴______________=_______________( )
又∵∠1=∠C ( )
∴∠2= ∠C ( )
∴BF∥AC ( )
3.如图,如果直线AB⊥BD,CD⊥BD,点B,D分别为垂足,那么直线AB和CD平
行吗?为什么?由此你能得到什么结论?
4.如图,AE平分∠CAB,CE平分∠ACD,且∠1+∠2=90°,说明AB与CD的位置
关系。
四、自我反思:你还有什么疑惑,同伴交流或请教老师
教学反思:
2
1
3
4
a
b
c
2
1
3
4
a
b
c
D
C
A
B
3
1
4
5
2
α
β
北
北
A
C
B
A
B
C
D
1
2
3
4
E
B
C
A
F
2
1
D
B
D
A
C
1
2
A
C
D
E
B
学科负责人签字:叶 飞 课改中心评价人___________ 得分(等级)_________
课 题:平行线的判定(三) 课型:预习+展示
主备人:叶 飞 备课时间:2011年 5 月 25 日
授课老师: 使用时间:
学习目标:1、在掌握平行线判定方法1的基础上,探讨利用内错角和同旁内角来判定两直线平行.
2.通过平行线判定2和判定3的推理过程进一步学会“说理”,以及理解蕴含其中的化归思想——把新问题转化为已经解决的问题;同时培养数学概括的能力.
学习重点:在掌握平行线的判定方法1的基础上,探讨利用内错角和同旁内角
来判定两直线平行.
学习难点:利用内错角和同旁内角来判定两直线平行.
学生学习过程:(课型不同,学习过程有所不同)
一、旧知回顾
平行线的判定方法1_________________________________________________
二,新知探究
1.如图:直线a、b被直线c所截,如果内错角∠2=∠4相等,那么直线a,b有怎样的位置关系?为什么?
a∥b
说明:∵直线a、b被直线c所截
∴∠1 = ∠2( )
∵∠2 = ∠4( )
∴∠_____ = ∠_____( )
∴a∥b ( )
由此,可得平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:______________________________________
2.如图:直线a、b被直线c所截,如果同旁内角∠3+∠4=180°,那么直线a,b有怎样的位置关系?为什么?
a∥b
说明:∵直线a、b被直线c所截
∴∠1+∠3=180°( )
∵∠3+∠4=180°( )
∴∠_____ = ∠_____( )
∴a∥b ( )
由此,可得平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说:______________________________________
三、例题学习
例1.看图填空
(1)∠1=∠2,可以得到________∥________,依据是_______________________;
(2)∠3=∠4,可以得到________∥________,依据是_______________________;
(3)∠5=∠DAB,可以得到________∥________,依据是____________________;
(4)要得到AD∥BC,需∠DAB+_______=180°,依据是____________________;
(5)要得到AB∥DC,需_______+_______=180°,依据是___________________;
例2.如图,一项筑路工程需要穿过山体挖一条隧道,甲,乙两个工程队分别从山体两侧的A,B两点同时开挖,现甲队从A点测得道路的走向是北偏东55°,问乙队在B点处应该按∠β是多少度开始挖掘,才能使隧道准确接通?
三、反馈练习
1.如图,已知∠1=50°,要使AB∥CD,则须具备另一个条件不成立的是( )
A ∠2=130° B ∠3=50° C ∠4=49° D ∠4=50°
2.如图,已知E、B、C三点共线,BE平分∠DBF,∠1=∠C,可以推出BF∥AC,推理过程如下:
∵BE平分∠DBF ( )
∴______________=_______________( )
又∵∠1=∠C ( )
∴∠2= ∠C ( )
∴BF∥AC ( )
3.如图,如果直线AB⊥BD,CD⊥BD,点B,D分别为垂足,那么直线AB和CD平
行吗?为什么?由此你能得到什么结论?
4.如图,AE平分∠CAB,CE平分∠ACD,且∠1+∠2=90°,说明AB与CD的位置
关系。
四、自我反思:你还有什么疑惑,同伴交流或请教老师
教学反思:
2
1
3
4
a
b
c
2
1
3
4
a
b
c
D
C
A
B
3
1
4
5
2
α
β
北
北
A
C
B
A
B
C
D
1
2
3
4
E
B
C
A
F
2
1
D
B
D
A
C
1
2
A
C
D
E
B
