11.5几何证明举例2

11.5几何证明举例2
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一学习目标：
1掌握证明直角三角全等的方法（HL）
2会用（HL）定理证明直角三角形全等。
3进一步掌握证明的书写格式。
二知识回顾：
全等三角形的判断方法1 、2 、3 、4 。
三 自主预习：
1如果一个直角三角形的斜边及 与另一个直角三角形的斜边及 对应相等，那么这两个直角三角形全等，此定理简记为“斜边、直角边”或“ ”
2线段的垂直平分线的定理与判定定理。
（1）线段垂直平分线上的点到这条线段 的距离相等。
（2）到一条线段两个端点的距离 的点，在这条线段 的平分线上。
四 导学探究：
探究 有关全等直角三角形的证明
与同学交流下列问题。
一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等，这两个直角三角形全等吗？
一个直角三角形的斜边和一条直角边与另一个直角三角的斜边和一条直角边对应相等，这两个直角三角形全等吗？无为什么？
已知：如图，在Rt△ABC和Rt△A′B′C′中，∠C和∠C′都是直角，AB＝A′B′，AC＝
A′C′.
求证：Rt△ABC≌Rt△ABC。
例3 求证：到一条线段两个端点的距离相等的点，在这条线段的垂直平分线上。
已知：如图，点P和线段AB，
求证：点P在线段AB的垂直平分线上。
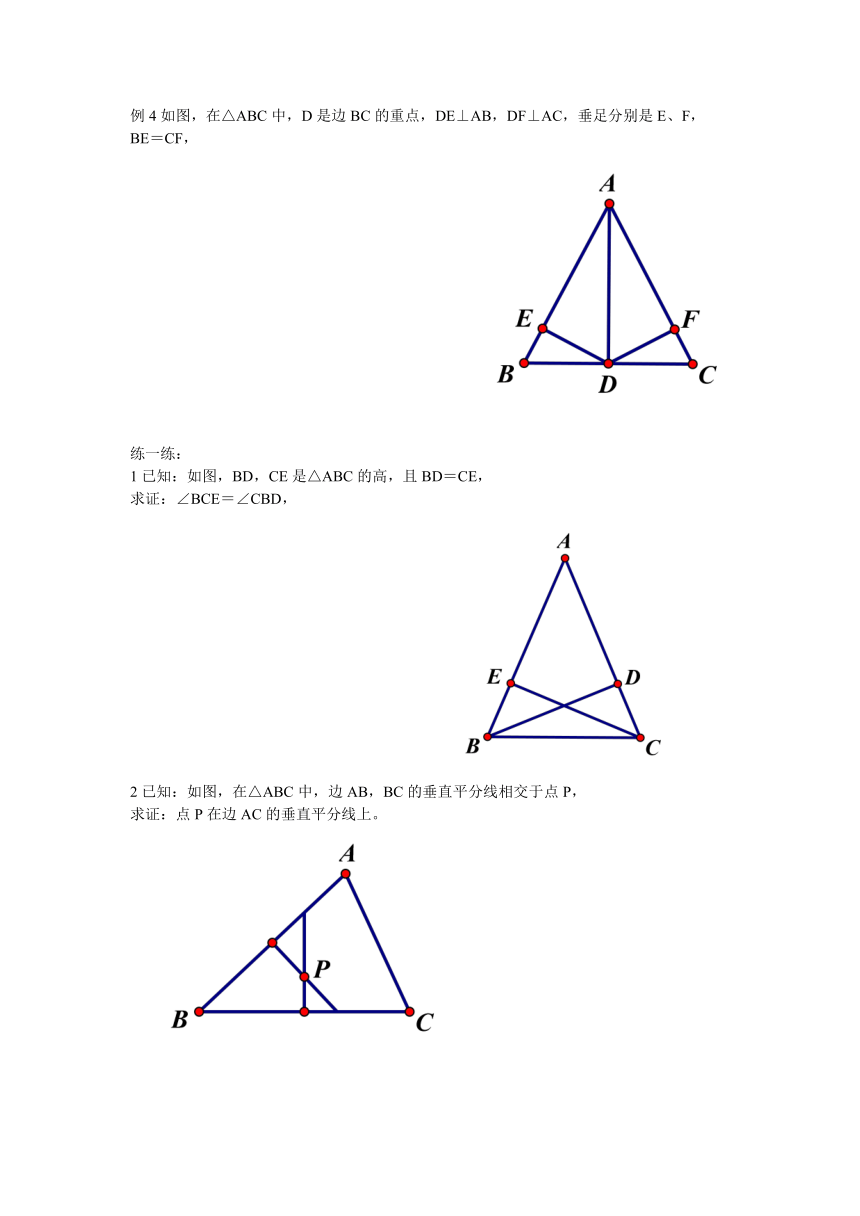
例4如图，在△ABC中，D是边BC的重点，DE⊥AB，DF⊥AC，垂足分别是E、F，
BE＝CF，
练一练：
1已知：如图，BD，CE是△ABC的高，且BD＝CE，
求证：∠BCE＝∠CBD，
2已知：如图，在△ABC中，边AB，BC的垂直平分线相交于点P，
求证：点P在边AC的垂直平分线上。
五 当堂达标
1如图∠BAD=∠BCD=900，AB=CD,可以证明△BAD≌△BCD的理由是( )
HL BASA CSAS DAAS
（１题图）　　　　　　　　　　　　　　　　　　　　　（３题图）
2下列命题正确的是（ ）
①线段的垂直平分线上任一点到线段两个端点的距离相等
②线段上的任一点到垂直平分线的两端点的距离相等
③经过线段中的的直线只有一条
④点P在线段AB外且PA=PB,过P作直线MN，则MN是线段AB的垂直平分线
⑤ 过线段上的任一点可以作线段的垂直平分线
A1个 B2个 C3个 D4个
3如图，在ABC中，AD⊥BC,CE⊥AB,垂足分别是D、E,AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是(　　　　　　　)
Ａ１　　　　Ｂ２　　　　　　Ｃ３　　　　　Ｄ４
４如图，已知ＣＤ⊥ＡＢ,ＢＥ⊥ＡＣ,垂足分别是Ｄ、Ｅ,ＢＥ、ＣＤ交于点Ｏ,且ＡＯ平分
∠ＢＡＣ,那么图中全等三角形共有　　　　　对
（４题图）　　　　　　　　　　　　　　　　　　（５题图）
５已知正方形ＡＢＣＤ中，点Ｅ在边ＤＣ上，ＤＥ=２，ＣＥ=１， 把线段ＡＥ绕点Ａ旋转，使点Ｅ落在直线ＢＣ上的点Ｆ处，则Ｆ、Ｃ
两点的距离为　　　　　　　。
６如图，已知矩形ＡＢＣＤ中，Ｅ是ＡＤ上的一点，Ｆ是ＡＢ上的一点，ＥＦ⊥ＥＣ,且ＥＦ=ＥＣ,ＤＥ=４ｃｍ，矩形ＡＢＣＤ的周长为３２ｃｍ，求ＡＥ的长。
７如图，已知在△ＡＢＣ中，∠ＡＣＢ=９０，ＣＤ⊥ＡＢ于点Ｄ,点Ｅ在ＡＣ上，ＣＥ=ＢＣ,过Ｅ点作ＡＣ得垂线，交ＣＤ的延长线与点Ｆ。求证:ＡＢ=ＣＤ
８如图，在△ＡＢＣ中，ＡＢ=ＣＤ,∠Ａ=３６０，线段ＡＢ的垂直平分线交ＡＢ于Ｄ,交ＡＣ于Ｅ,连接ＢＥ.
求证：∠ＣＢＥ=３６０
求证：ＡＥ２=ＡＣ·ＥＣ
A′
B′
C′
A
B
C
P
A
B
C
┐
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
Ｈ
A
B
C
D
┐
┐
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
Ｏ
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
Ｆ
Ａ
Ｂ
Ｃ
Ｆ
Ｅ
Ｄ
Ａ
Ｂ
Ｃ
Ｄ
Ｅ