北师大版八年级下册数学 第六章 平行四边形之三角形中位线及多边形内角和与外角和复习课件 (共18张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 第六章 平行四边形之三角形中位线及多边形内角和与外角和复习课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
三角形中位线及多边形
内角和与外角和---复习课
北师大版八年级数学下册
学习目标
1.理解三角形中位线的定义
2.掌握三角形中位线定理并能够熟练运用
3.通过题组训练,能够熟练掌握多边形内角和定理和外角和定理
知识回顾
1.定义:_________________叫做三角形的中位线。
2.三角形中位线定理:三角形的中位线_______第 三边,且等于______________。
4.多边形的外角和等于__________。
3.多边形的内角和定理:
n边形的内角和等于 _______________。
连接三角形两边中点的线段
平行于
第三边的一半
(n-2)·180°
360°
经典例题:
让你的思维做体操
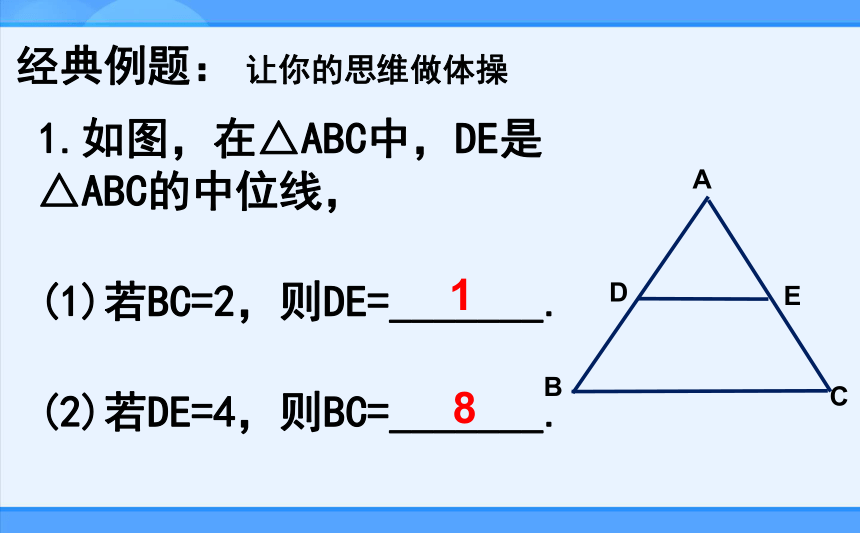
1.如图,在△ABC中,DE是
△ABC的中位线,
(1)若BC=2,则DE=_______.
(2)若DE=4,则BC=_______.
1
8
C
E
B
A
D
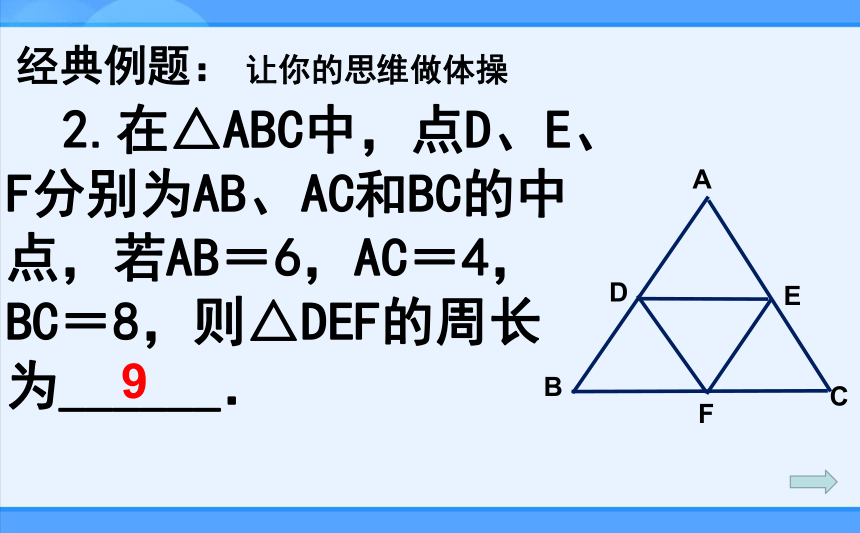
2.在△ABC中,点D、E、F分别为AB、AC和BC的中点,若AB=6,AC=4,BC=8,则△DEF的周长为______.
经典例题:
让你的思维做体操
C
E
B
A
D
F
9
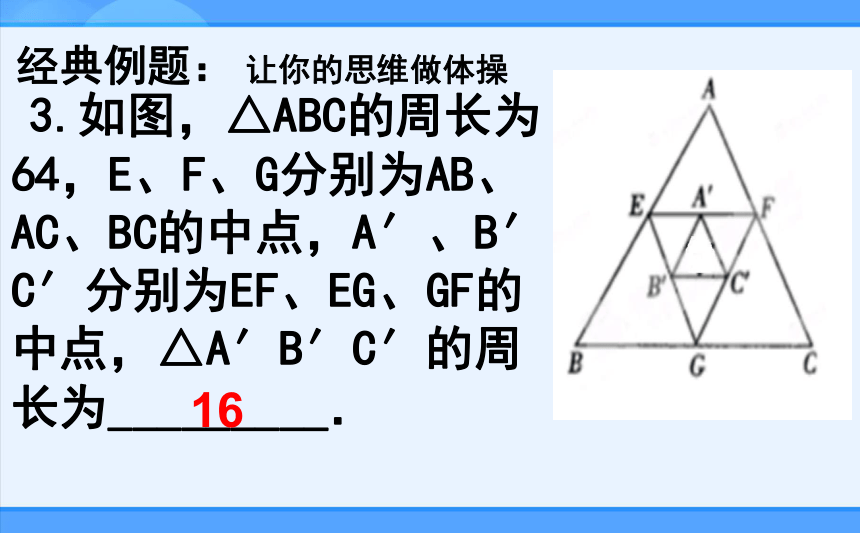
3.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.
经典例题:
让你的思维做体操
16
4.一个多边形的内角和等于外角和的3倍,这个多边形是________边形。
经典例题:
让你的思维做体操
八
证明:
∵四边形ABCD是平行四边形(已知)
∴ OA=OC(平行四边形的对角线互相平分)
∵AE=EB(已知)
∴EO是△ABC的中位线(中位线的定义)
∴ OE∥BC, OE= BC(三角形的中位线平行于第三边,并且等于第三边的一半).
5.如图所示,□ ABCD的对角线AC,BD相交于点O,AE=EB.试说明OE与BC的关系.
中考链接
当堂训练:
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,则∠B= ____ 度.
(2)若BC=8cm,则DE= ______ cm.
2.如图2:在△ABC中,D、E、F分别是各边中点. AB=6cm,AC=6cm,BC=8cm,
则△DEF的周长= _________ cm.
3.在一张三角形纸片中,剪去其中一个50°的角,得到如图所示的四边形,则图中∠1+∠2的度数为____________度.
60
4
10
230
当堂训练:
5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= __________.
6.如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是_________.
4.若一个多边形内角和等于1260°,则该多边形边数 是_______.
9
360°
28米
当堂训练:
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A. 6cm B. 12cm C. 18cm D. 36cm
8.已知一个多边形的内角和是540°,则这个多边形是
( )
A. 四边形 B. 五边形
C. 六边形 D. 七边形
9.七边形内角和的度数是( )
A. 1 080° B. 1 260° C. 1 620° D. 900°
C
B
D
10.已知一个多边形的内角和与外角和之和为2160°,求这个多边形的边数。
当堂训练:
解:设这个多边形的边数为n ,则
(n-2)×180°+360°=2160°
(n-2)×180°=1800°
(n-2)=10
n=12
答:这个多边形的边数是12.
当堂训练:
11.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形。
证明:∵BD和CE是△ABC的中线
∴DE是△ABC的中位线
∴ DE∥BC, DE= BC
又∵F、G分别是OB、OC的中点
∴FG是△OBC的中位线
∴ FG∥BC, FG= BC
∴ DE∥FG, DE=FG
∴四边形DEFG是平行四边形
实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?
A
B
(1)在A、B外选一点C,连结AC和BC ;
C
M
N
(2)并分别找出AC和BC的中点M、N 。
(3)连结MN ,并测量MN的长度。
解决方案
拓展创新
A
B
(1)在A、B外选一点C,连结AC并延长至点N,使得CN=AC ;连接BC并延长至点M,使得CM=BC;
(2)连接MN,并测量MN的长度。
C
解决方案
拓
展
创
新
M
N
三角形中位线及多边形
内角和与外角和---复习课
北师大版八年级数学下册
学习目标
1.理解三角形中位线的定义
2.掌握三角形中位线定理并能够熟练运用
3.通过题组训练,能够熟练掌握多边形内角和定理和外角和定理
知识回顾
1.定义:_________________叫做三角形的中位线。
2.三角形中位线定理:三角形的中位线_______第 三边,且等于______________。
4.多边形的外角和等于__________。
3.多边形的内角和定理:
n边形的内角和等于 _______________。
连接三角形两边中点的线段
平行于
第三边的一半
(n-2)·180°
360°
经典例题:
让你的思维做体操
1.如图,在△ABC中,DE是
△ABC的中位线,
(1)若BC=2,则DE=_______.
(2)若DE=4,则BC=_______.
1
8
C
E
B
A
D
2.在△ABC中,点D、E、F分别为AB、AC和BC的中点,若AB=6,AC=4,BC=8,则△DEF的周长为______.
经典例题:
让你的思维做体操
C
E
B
A
D
F
9
3.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.
经典例题:
让你的思维做体操
16
4.一个多边形的内角和等于外角和的3倍,这个多边形是________边形。
经典例题:
让你的思维做体操
八
证明:
∵四边形ABCD是平行四边形(已知)
∴ OA=OC(平行四边形的对角线互相平分)
∵AE=EB(已知)
∴EO是△ABC的中位线(中位线的定义)
∴ OE∥BC, OE= BC(三角形的中位线平行于第三边,并且等于第三边的一半).
5.如图所示,□ ABCD的对角线AC,BD相交于点O,AE=EB.试说明OE与BC的关系.
中考链接
当堂训练:
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,则∠B= ____ 度.
(2)若BC=8cm,则DE= ______ cm.
2.如图2:在△ABC中,D、E、F分别是各边中点. AB=6cm,AC=6cm,BC=8cm,
则△DEF的周长= _________ cm.
3.在一张三角形纸片中,剪去其中一个50°的角,得到如图所示的四边形,则图中∠1+∠2的度数为____________度.
60
4
10
230
当堂训练:
5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= __________.
6.如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是_________.
4.若一个多边形内角和等于1260°,则该多边形边数 是_______.
9
360°
28米
当堂训练:
7.一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是( )
A. 6cm B. 12cm C. 18cm D. 36cm
8.已知一个多边形的内角和是540°,则这个多边形是
( )
A. 四边形 B. 五边形
C. 六边形 D. 七边形
9.七边形内角和的度数是( )
A. 1 080° B. 1 260° C. 1 620° D. 900°
C
B
D
10.已知一个多边形的内角和与外角和之和为2160°,求这个多边形的边数。
当堂训练:
解:设这个多边形的边数为n ,则
(n-2)×180°+360°=2160°
(n-2)×180°=1800°
(n-2)=10
n=12
答:这个多边形的边数是12.
当堂训练:
11.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形。
证明:∵BD和CE是△ABC的中线
∴DE是△ABC的中位线
∴ DE∥BC, DE= BC
又∵F、G分别是OB、OC的中点
∴FG是△OBC的中位线
∴ FG∥BC, FG= BC
∴ DE∥FG, DE=FG
∴四边形DEFG是平行四边形
实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?
A
B
(1)在A、B外选一点C,连结AC和BC ;
C
M
N
(2)并分别找出AC和BC的中点M、N 。
(3)连结MN ,并测量MN的长度。
解决方案
拓展创新
A
B
(1)在A、B外选一点C,连结AC并延长至点N,使得CN=AC ;连接BC并延长至点M,使得CM=BC;
(2)连接MN,并测量MN的长度。
C
解决方案
拓
展
创
新
M
N
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
