19.2.3 正方形公开课
文档属性
| 名称 | 19.2.3 正方形公开课 |

|
|
| 格式 | rar | ||
| 文件大小 | 260.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-27 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
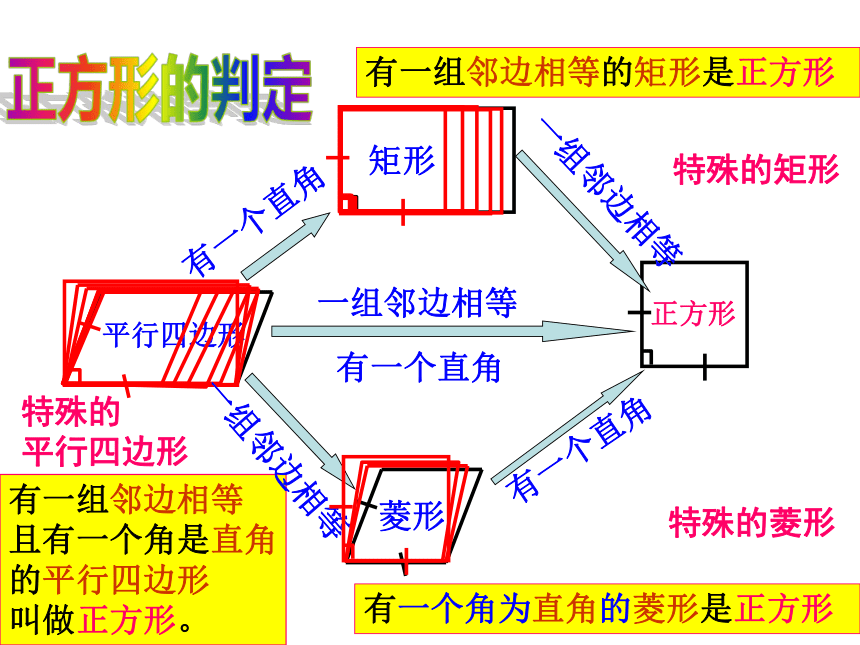
有一组邻边相等
且有一个角是直角
的平行四边形
叫做正方形。
平行四边形
有一个直角
矩形
一组邻边相等
菱形
一组邻边相等
正方形
有一个直角
有一组邻边相等的矩形是正方形
有一个角为直角的菱形是正方形
特殊的矩形
特殊的菱形
特殊的
平行四边形
一组邻边相等
有一个直角
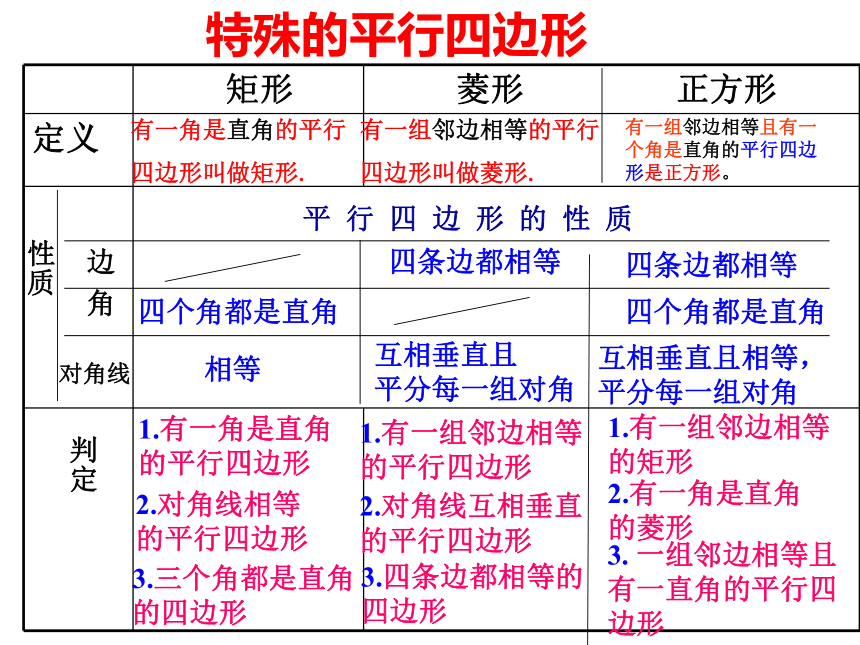
特殊的平行四边形
矩形 菱形 正方形
定义
有一角是直角的平行
四边形叫做矩形.
有一组邻边相等的平行
四边形叫做菱形.
平 行 四 边 形 的 性 质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且
平分每一组对角
判定
四条边都相等
有一组邻边相等且有一个角是直角的平行四边形是正方形。
四条边都相等
四个角都是直角
互相垂直且相等,平分每一组对角
1.有一角是直角的平行四边形
2.对角线相等的平行四边形
3.三个角都是直角的四边形
1.有一组邻边相等的平行四边形
2.对角线互相垂直的平行四边形
3.四条边都相等的四边形
1.有一组邻边相等的矩形
2.有一角是直角的菱形
3. 一组邻边相等且有一直角的平行四边形
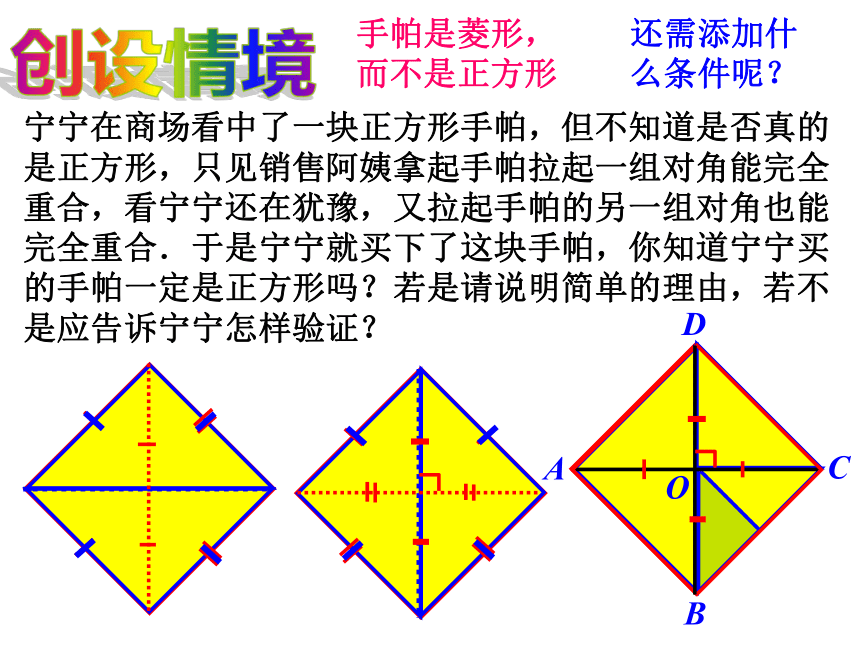
宁宁在商场看中了一块正方形手帕,但不知道是否真的是正方形,只见销售阿姨拿起手帕拉起一组对角能完全重合,看宁宁还在犹豫,又拉起手帕的另一组对角也能完全重合.于是宁宁就买下了这块手帕,你知道宁宁买的手帕一定是正方形吗?若是请说明简单的理由,若不是应告诉宁宁怎样验证?
手帕是菱形,而不是正方形
还需添加什么条件呢?
A
B
C
D
O
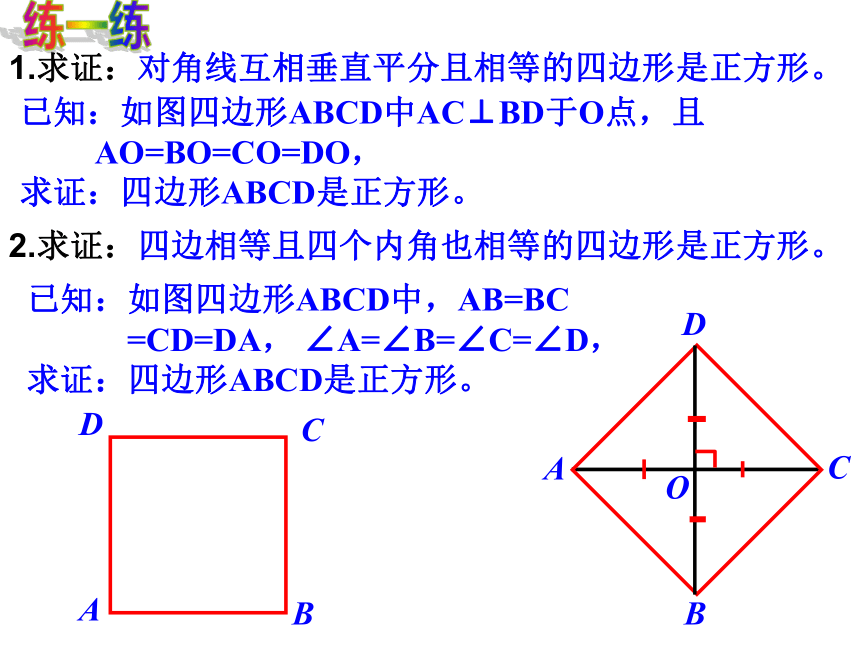
1.求证:对角线互相垂直平分且相等的四边形是正方形。
已知:如图四边形ABCD中AC⊥BD于O点,且
AO=BO=CO=DO,
求证:四边形ABCD是正方形。
2.求证:四边相等且四个内角也相等的四边形是正方形。
A
D
C
B
已知:如图四边形ABCD中,AB=BC
=CD=DA, ∠A=∠B=∠C=∠D,
求证:四边形ABCD是正方形。
A
B
C
D
O
①、对角线相等的菱形是正方形
②、对角线互相垂直的矩形是正方形
③、对角线互相垂直且相等的四边形是正方形
④ 四条边都相等的四边形是正方形
⑤、四个角都相等的四边形是正方形
⑥、四边相等,有一个角是直角的四边形是正方形.
( )
( )
( )
( )
( )
( )
3.判断下列命题哪些是真命题、哪些是假命题?
真
真
假
假
假
真
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
×
×
√
√
4、判断题:
5、在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
例1.如图,正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
AB=BC,∠1=∠2=45 °
AM=BN
△ABM≌△BCN
正方形ABCD
OM=ON
∠OMN=∠ONM=45°
A
B
D
C
O
M
N
1
2
45°
45°
45°
45°
练1: 正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF
(2)若E是OB的延长线上的一点, OE = OF还成立吗
E
A
B
C
D
O
G
F
1
2
3
A
B
C
D
O
E
G
F
证明:∵四边形ABDE和四边形ACFG是正方形。
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
例2.如图△ABC的外面作正方形ABDE和ACFG,连结BG、 CE,交点为N. 求证:∠CEA=∠ABG
1
A
N
G
F
C
B
E
D
2
CE与BG有何关系
垂直且相等
练2:如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD,延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF
E
D
A
C
B
G
F
H
练习1:(1)如图,点E、F在正方形ABCD的边BC、CD上,AE=BF.求证:AE⊥BF
(2)如图,点E、F在正方形ABCD的边BC、CD上, AE⊥BF.求证: AE=BF
(3)若图形变为图2与图3时,上两题结论还成立吗?
A
B
C
D
E
F
G
A
B
C
D
E
F
G
B1
A
B
C
D
E
F
G
B1
A1
F1
F1
G1
G1
G2
E1
活动与探索
练习2:已知正方形ABCD,延长AB到F,连结FC,作AG⊥FC于G,AG交BC于E,
求证(1)AE=CF
A
B
C
D
E
F
G
(2)∠BEF=45°
活动与探索
3.在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
(1)试说明:DE=DF
(2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
活动与探索
例2、在矩形ABCD中,P是AD上的一个动点,PE⊥ AC于E,PF⊥ BD于F,AG⊥ BD于G。试问,PE+PF与AG有什么关系?证明你的结论。
A
B
C
D
E
F
G
O
P
典型例题
4、如图,BD、CE是△ABC的高,G 、 F
分别是BC、DE的中点,求证:FG⊥DE.
A
E
B
G
C
D
F
巩固练习
活动与探索
A
B
C
D
E
F
2.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=45°
变式:3.如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=45°,△CEF的面积为 ,
求△AEF的面积。
G
1
2
45°
45°
有一组邻边相等
且有一个角是直角
的平行四边形
叫做正方形。
平行四边形
有一个直角
矩形
一组邻边相等
菱形
一组邻边相等
正方形
有一个直角
有一组邻边相等的矩形是正方形
有一个角为直角的菱形是正方形
特殊的矩形
特殊的菱形
特殊的
平行四边形
一组邻边相等
有一个直角
特殊的平行四边形
矩形 菱形 正方形
定义
有一角是直角的平行
四边形叫做矩形.
有一组邻边相等的平行
四边形叫做菱形.
平 行 四 边 形 的 性 质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且
平分每一组对角
判定
四条边都相等
有一组邻边相等且有一个角是直角的平行四边形是正方形。
四条边都相等
四个角都是直角
互相垂直且相等,平分每一组对角
1.有一角是直角的平行四边形
2.对角线相等的平行四边形
3.三个角都是直角的四边形
1.有一组邻边相等的平行四边形
2.对角线互相垂直的平行四边形
3.四条边都相等的四边形
1.有一组邻边相等的矩形
2.有一角是直角的菱形
3. 一组邻边相等且有一直角的平行四边形
宁宁在商场看中了一块正方形手帕,但不知道是否真的是正方形,只见销售阿姨拿起手帕拉起一组对角能完全重合,看宁宁还在犹豫,又拉起手帕的另一组对角也能完全重合.于是宁宁就买下了这块手帕,你知道宁宁买的手帕一定是正方形吗?若是请说明简单的理由,若不是应告诉宁宁怎样验证?
手帕是菱形,而不是正方形
还需添加什么条件呢?
A
B
C
D
O
1.求证:对角线互相垂直平分且相等的四边形是正方形。
已知:如图四边形ABCD中AC⊥BD于O点,且
AO=BO=CO=DO,
求证:四边形ABCD是正方形。
2.求证:四边相等且四个内角也相等的四边形是正方形。
A
D
C
B
已知:如图四边形ABCD中,AB=BC
=CD=DA, ∠A=∠B=∠C=∠D,
求证:四边形ABCD是正方形。
A
B
C
D
O
①、对角线相等的菱形是正方形
②、对角线互相垂直的矩形是正方形
③、对角线互相垂直且相等的四边形是正方形
④ 四条边都相等的四边形是正方形
⑤、四个角都相等的四边形是正方形
⑥、四边相等,有一个角是直角的四边形是正方形.
( )
( )
( )
( )
( )
( )
3.判断下列命题哪些是真命题、哪些是假命题?
真
真
假
假
假
真
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
×
×
√
√
4、判断题:
5、在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
例1.如图,正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
AB=BC,∠1=∠2=45 °
AM=BN
△ABM≌△BCN
正方形ABCD
OM=ON
∠OMN=∠ONM=45°
A
B
D
C
O
M
N
1
2
45°
45°
45°
45°
练1: 正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF
(2)若E是OB的延长线上的一点, OE = OF还成立吗
E
A
B
C
D
O
G
F
1
2
3
A
B
C
D
O
E
G
F
证明:∵四边形ABDE和四边形ACFG是正方形。
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
例2.如图△ABC的外面作正方形ABDE和ACFG,连结BG、 CE,交点为N. 求证:∠CEA=∠ABG
1
A
N
G
F
C
B
E
D
2
CE与BG有何关系
垂直且相等
练2:如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD,延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF
E
D
A
C
B
G
F
H
练习1:(1)如图,点E、F在正方形ABCD的边BC、CD上,AE=BF.求证:AE⊥BF
(2)如图,点E、F在正方形ABCD的边BC、CD上, AE⊥BF.求证: AE=BF
(3)若图形变为图2与图3时,上两题结论还成立吗?
A
B
C
D
E
F
G
A
B
C
D
E
F
G
B1
A
B
C
D
E
F
G
B1
A1
F1
F1
G1
G1
G2
E1
活动与探索
练习2:已知正方形ABCD,延长AB到F,连结FC,作AG⊥FC于G,AG交BC于E,
求证(1)AE=CF
A
B
C
D
E
F
G
(2)∠BEF=45°
活动与探索
3.在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
(1)试说明:DE=DF
(2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
活动与探索
例2、在矩形ABCD中,P是AD上的一个动点,PE⊥ AC于E,PF⊥ BD于F,AG⊥ BD于G。试问,PE+PF与AG有什么关系?证明你的结论。
A
B
C
D
E
F
G
O
P
典型例题
4、如图,BD、CE是△ABC的高,G 、 F
分别是BC、DE的中点,求证:FG⊥DE.
A
E
B
G
C
D
F
巩固练习
活动与探索
A
B
C
D
E
F
2.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=45°
变式:3.如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=45°,△CEF的面积为 ,
求△AEF的面积。
G
1
2
45°
45°
