鲁教版(五四制)数学八年级上册第三章数据的分析达标测试卷 含答案
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册第三章数据的分析达标测试卷 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 13:49:13 | ||
图片预览




文档简介
第三章达标测试卷
一、选择题(每题3分,共30分)
1.有一组数据:1,3,3,4,5.这组数据的众数为( )
A.1
B.3
C.4
D.5
2.小明记录了当地今年元月份某五天的最低温度(单位:℃):1,2,0,-1,-2.这五天最低温度数据的平均数是( )
A.1
B.2
C.0
D.-1
3.某校为纪念世界反法西斯战争胜利70周年,举行了主题为“让历史照亮未来”的演讲比赛,其中九年级的5位参赛选手的比赛成绩(单位:分)分别为8.6,9.5,9.7,8.8,9,则这5个数据的中位数是( )
A.9.7
B.9.5
C.9
D.8.8
4.某制鞋厂准备生产一批男皮鞋,经抽样(120名中年男子)调查得知,所需鞋号和人数如下:
鞋号/cm
24
24.5
25
25.5
26
26.5
27
人数
8
15
20
25
30
20
2
现求出鞋号的中位数是25.5
cm,众数是26
cm,平均数约是25.5
cm.下列说法正确的是( )
A.因为需要鞋号为27
cm的人数太少,所以鞋号为27
cm的鞋可以不生产
B.因为平均数约是25.5
cm,所以这批男鞋可以一律按鞋号为25.5
cm的鞋生产
C.因为中位数是25.5
cm,所以25.5
cm的鞋的生产量应占首位
D.因为众数是26
cm,所以26
cm的鞋的生产量应占首位
5.某校规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )
A.89分
B.90分
C.92分
D.93分
6.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,那么应选择的学生是( )
A.甲
B.乙
C.丙
D.丁
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
A.4,4
B.3,4
C.4,3
D.3,3
8.某小组5位同学参加实验操作考试(满分20分)的平均成绩是16分,其中三位男生成绩的方差为6,两位女生的成绩分别为17分、15分,则这5位同学成绩的标准差为( )
A.
B.2
C.
D.6
9.如果一组数据a1,a2,a3,…,an的方差是2,那么一组新数据2a1,2a2,2a3,…,2an的方差是( )
A.2
B.4
C.8
D.16
10.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁.经重新计算后,正确的平均数为a岁,中位数为b岁.则下列结论中正确的是( )
A.a<13,b=13
B.a<13,b<13
C.a>13,b<13
D.a>13,b=13
二、填空题(每题3分,共24分)
11.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为5,7,9,10,7,则这组数据的众数是________.
12.一组数据-1,0,1,2,x的众数是2,则这组数据的平均数是________.
13.已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是________.
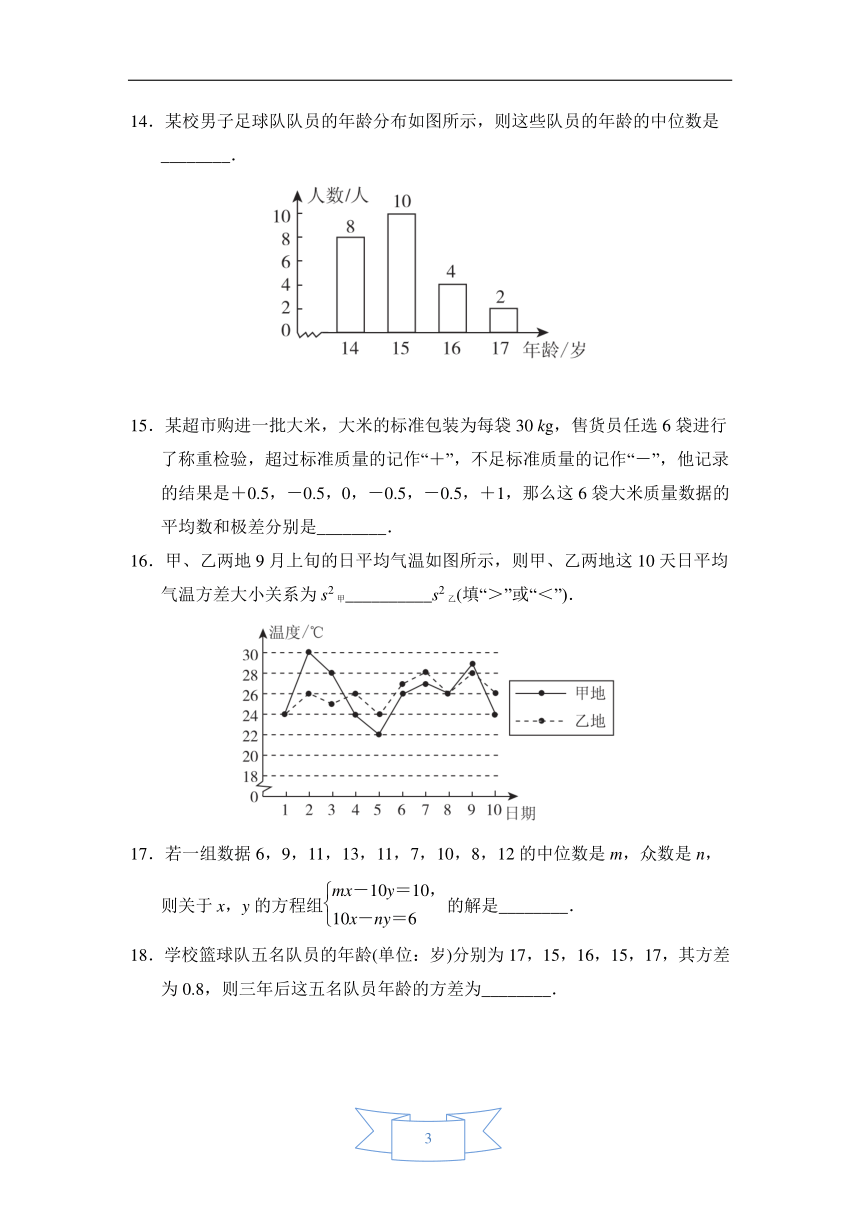
14.某校男子足球队队员的年龄分布如图所示,则这些队员的年龄的中位数是________.
15.某超市购进一批大米,大米的标准包装为每袋30
kg,售货员任选6袋进行了称重检验,超过标准质量的记作“+”,不足标准质量的记作“-”,他记录的结果是+0.5,-0.5,0,-0.5,-0.5,+1,那么这6袋大米质量数据的平均数和极差分别是________.
16.甲、乙两地9月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温方差大小关系为s2甲__________s2乙(填“>”或“<”).
17.若一组数据6,9,11,13,11,7,10,8,12的中位数是m,众数是n,则关于x,y的方程组的解是________.
18.学校篮球队五名队员的年龄(单位:岁)分别为17,15,16,15,17,其方差为0.8,则三年后这五名队员年龄的方差为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.一个电梯的最大载质量是1
000
kg,现有平均体重为80
kg的11人和平均体重为70
kg的2人,他们能否一起搭乘这个电梯?他们的平均体重是多少千克?(结果精确到0.1
kg)
20.八年级(2)班组织了一场经典诵读比赛,甲、乙两队各10人的比赛成绩(10分制,单位:分)如下表:
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是________分,乙队成绩的众数是________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是________队.
21.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组的各项得分(单位:分)如下表:
小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
22.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲
95
82
88
81
93
79
84
78
乙
83
92
80
95
90
80
85
75
(1)请你计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从稳定性的角度考虑,你认为选派谁参加比较合适?请说明理由.
23.已知一组数据x1,x2,…,x6的平均数为1,方差为.
(1)求x21+x22+…+x26的值;
(2)若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差(结果用分数表示).
24.荆门市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图如图所示,成绩统计分析表如表所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分/分
中位数/分
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说:“七年级代表队的合格率、优秀率均高于八年级代表队,所以七年级代表队的成绩比八年级代表队好.”但也有人说:“八年级代表队的成绩比七年级队好.”请你给出两条支持八年级代表队成绩好的理由.
答案
一、1.B 2.C 3.C 4.D 5.B
6.B 7.D 8.B 9.C 10.A
二、11.7 12.0.8 13.
14.15岁 15.30;1.5 16.>
17. 点拨:这组数据按从小到大的顺序排列为6,7,8,9,10,11,11,12,13.由题意得m=10,n=11.
由
解得
18.0.8
三、19.解:80×11+70×2=1
020(kg),1
020
kg>1
000
kg,所以他们不能一起搭乘这个电梯.
他们的平均体重为1
020÷(11+2)≈78.5(kg).
20.解:(1)9.5;10
(2)x乙=
=
9(分).
s2乙=×[(10-9)2+(8-9)2+…+(9-9)2]=1.
(3)乙
21.解:(1)由题意可得,
x甲==83(分),
x乙==80(分),
x丙==84(分).
∵x丙>x甲>x乙,
∴从高分到低分确定小组的排名顺序为丙、甲、乙.
(2)甲组的成绩是91×40%+
80×30%+78×30%=83.8(分),
乙组的成绩是81×40%+74×30%+85×30%=80.1(分),丙组的成绩是79×40%+83×30%+90×30%=83.5(分).
∵83.8>83.5>80.1
∴甲组的成绩最高.
22.解:(1)x甲=×(95+82+88+81+93+79+84+78)=85;
x乙=×(83+92+80+95+90+80+85+75)=85.
这两组数据的平均数都是85.
(2)(答案不唯一)选派甲参加比较合适.
理由如下:由(1)知x甲=x乙=85,则s2甲=×[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,s2乙=×[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41,
∴s2甲∴甲的成绩较稳定,
∴选派甲参加比较合适.
23.解:(1)∵数据x1,x2,…,x6的平均数为1,
∴x1+x2+…+x6=1×6=6.
又∵方差为,
∴[(x1-1)2+(x2-1)2+
…+(x6-1)2]=[x21+x22+…+x26-2(x1+x2+…+x6)+6]=(x21+x22+…+x26-2×
6+6)=(x21+x22+…+x26)-1=,
∴x21+x22+…+x26=16.
(2)∵数据x1,x2,…,x7的平均数为1,
∴x1+x2+…+x7=1×7=7.∵x1+x2+…+x6=6,
∴x7=1.∵[(x1-1)2+(x2-1)2+…+(x6-1)2]=,
∴(x1-1)2+(x2-1)2+…+(x6-1)2=10,
∴s2=[(x1-1)2+(x2-1)2+…+(x7-1)2]=[10+(1-1)2]=.
24.解:(1)依题意得
解得
(2)m=6,n=20%.
(3)(答案不唯一)①八年级代表队的平均分高于七年级代表队;②八年级代表队的成绩比七年级代表队稳定.
一、选择题(每题3分,共30分)
1.有一组数据:1,3,3,4,5.这组数据的众数为( )
A.1
B.3
C.4
D.5
2.小明记录了当地今年元月份某五天的最低温度(单位:℃):1,2,0,-1,-2.这五天最低温度数据的平均数是( )
A.1
B.2
C.0
D.-1
3.某校为纪念世界反法西斯战争胜利70周年,举行了主题为“让历史照亮未来”的演讲比赛,其中九年级的5位参赛选手的比赛成绩(单位:分)分别为8.6,9.5,9.7,8.8,9,则这5个数据的中位数是( )
A.9.7
B.9.5
C.9
D.8.8
4.某制鞋厂准备生产一批男皮鞋,经抽样(120名中年男子)调查得知,所需鞋号和人数如下:
鞋号/cm
24
24.5
25
25.5
26
26.5
27
人数
8
15
20
25
30
20
2
现求出鞋号的中位数是25.5
cm,众数是26
cm,平均数约是25.5
cm.下列说法正确的是( )
A.因为需要鞋号为27
cm的人数太少,所以鞋号为27
cm的鞋可以不生产
B.因为平均数约是25.5
cm,所以这批男鞋可以一律按鞋号为25.5
cm的鞋生产
C.因为中位数是25.5
cm,所以25.5
cm的鞋的生产量应占首位
D.因为众数是26
cm,所以26
cm的鞋的生产量应占首位
5.某校规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的这三项成绩(百分制)分别为95分,90分,88分,则小彤这学期的体育成绩为( )
A.89分
B.90分
C.92分
D.93分
6.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,那么应选择的学生是( )
A.甲
B.乙
C.丙
D.丁
7.已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别是( )
A.4,4
B.3,4
C.4,3
D.3,3
8.某小组5位同学参加实验操作考试(满分20分)的平均成绩是16分,其中三位男生成绩的方差为6,两位女生的成绩分别为17分、15分,则这5位同学成绩的标准差为( )
A.
B.2
C.
D.6
9.如果一组数据a1,a2,a3,…,an的方差是2,那么一组新数据2a1,2a2,2a3,…,2an的方差是( )
A.2
B.4
C.8
D.16
10.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁.经重新计算后,正确的平均数为a岁,中位数为b岁.则下列结论中正确的是( )
A.a<13,b=13
B.a<13,b<13
C.a>13,b<13
D.a>13,b=13
二、填空题(每题3分,共24分)
11.高一新生入学军训射击训练中,小张同学的射击成绩(单位:环)为5,7,9,10,7,则这组数据的众数是________.
12.一组数据-1,0,1,2,x的众数是2,则这组数据的平均数是________.
13.已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是________.
14.某校男子足球队队员的年龄分布如图所示,则这些队员的年龄的中位数是________.
15.某超市购进一批大米,大米的标准包装为每袋30
kg,售货员任选6袋进行了称重检验,超过标准质量的记作“+”,不足标准质量的记作“-”,他记录的结果是+0.5,-0.5,0,-0.5,-0.5,+1,那么这6袋大米质量数据的平均数和极差分别是________.
16.甲、乙两地9月上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温方差大小关系为s2甲__________s2乙(填“>”或“<”).
17.若一组数据6,9,11,13,11,7,10,8,12的中位数是m,众数是n,则关于x,y的方程组的解是________.
18.学校篮球队五名队员的年龄(单位:岁)分别为17,15,16,15,17,其方差为0.8,则三年后这五名队员年龄的方差为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.一个电梯的最大载质量是1
000
kg,现有平均体重为80
kg的11人和平均体重为70
kg的2人,他们能否一起搭乘这个电梯?他们的平均体重是多少千克?(结果精确到0.1
kg)
20.八年级(2)班组织了一场经典诵读比赛,甲、乙两队各10人的比赛成绩(10分制,单位:分)如下表:
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是________分,乙队成绩的众数是________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是________队.
21.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组的各项得分(单位:分)如下表:
小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
22.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲
95
82
88
81
93
79
84
78
乙
83
92
80
95
90
80
85
75
(1)请你计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从稳定性的角度考虑,你认为选派谁参加比较合适?请说明理由.
23.已知一组数据x1,x2,…,x6的平均数为1,方差为.
(1)求x21+x22+…+x26的值;
(2)若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差(结果用分数表示).
24.荆门市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图如图所示,成绩统计分析表如表所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分/分
中位数/分
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说:“七年级代表队的合格率、优秀率均高于八年级代表队,所以七年级代表队的成绩比八年级代表队好.”但也有人说:“八年级代表队的成绩比七年级队好.”请你给出两条支持八年级代表队成绩好的理由.
答案
一、1.B 2.C 3.C 4.D 5.B
6.B 7.D 8.B 9.C 10.A
二、11.7 12.0.8 13.
14.15岁 15.30;1.5 16.>
17. 点拨:这组数据按从小到大的顺序排列为6,7,8,9,10,11,11,12,13.由题意得m=10,n=11.
由
解得
18.0.8
三、19.解:80×11+70×2=1
020(kg),1
020
kg>1
000
kg,所以他们不能一起搭乘这个电梯.
他们的平均体重为1
020÷(11+2)≈78.5(kg).
20.解:(1)9.5;10
(2)x乙=
=
9(分).
s2乙=×[(10-9)2+(8-9)2+…+(9-9)2]=1.
(3)乙
21.解:(1)由题意可得,
x甲==83(分),
x乙==80(分),
x丙==84(分).
∵x丙>x甲>x乙,
∴从高分到低分确定小组的排名顺序为丙、甲、乙.
(2)甲组的成绩是91×40%+
80×30%+78×30%=83.8(分),
乙组的成绩是81×40%+74×30%+85×30%=80.1(分),丙组的成绩是79×40%+83×30%+90×30%=83.5(分).
∵83.8>83.5>80.1
∴甲组的成绩最高.
22.解:(1)x甲=×(95+82+88+81+93+79+84+78)=85;
x乙=×(83+92+80+95+90+80+85+75)=85.
这两组数据的平均数都是85.
(2)(答案不唯一)选派甲参加比较合适.
理由如下:由(1)知x甲=x乙=85,则s2甲=×[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,s2乙=×[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41,
∴s2甲
∴选派甲参加比较合适.
23.解:(1)∵数据x1,x2,…,x6的平均数为1,
∴x1+x2+…+x6=1×6=6.
又∵方差为,
∴[(x1-1)2+(x2-1)2+
…+(x6-1)2]=[x21+x22+…+x26-2(x1+x2+…+x6)+6]=(x21+x22+…+x26-2×
6+6)=(x21+x22+…+x26)-1=,
∴x21+x22+…+x26=16.
(2)∵数据x1,x2,…,x7的平均数为1,
∴x1+x2+…+x7=1×7=7.∵x1+x2+…+x6=6,
∴x7=1.∵[(x1-1)2+(x2-1)2+…+(x6-1)2]=,
∴(x1-1)2+(x2-1)2+…+(x6-1)2=10,
∴s2=[(x1-1)2+(x2-1)2+…+(x7-1)2]=[10+(1-1)2]=.
24.解:(1)依题意得
解得
(2)m=6,n=20%.
(3)(答案不唯一)①八年级代表队的平均分高于七年级代表队;②八年级代表队的成绩比七年级代表队稳定.
