相似三角形的判定(第4课时)
文档属性
| 名称 | 相似三角形的判定(第4课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 34.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-27 00:00:00 | ||
图片预览

文档简介
27.2.1相似三角形的判定(第4课时)
蒋良金
一、教学目标
知识与技能
初步掌握“两角对应相等,两个三角形相似”的判定方法.
过程与方法
能够运用三角形相似的条件解决简单的问题.
情感态度与价值观
经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
二、重点难点
重点
掌握判定方法,会运用判定方法判定两个三角形相似.
难点
会准确的运用两个三角形相似的条件来判定三角形是否相似.
四、教学过程设计
教学环节 问 题 设 计 师 生 活 动 备注
情境创设 观察两副三角板,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小不同,它们相似吗? 创设问题情境,引起学生学习的兴趣.
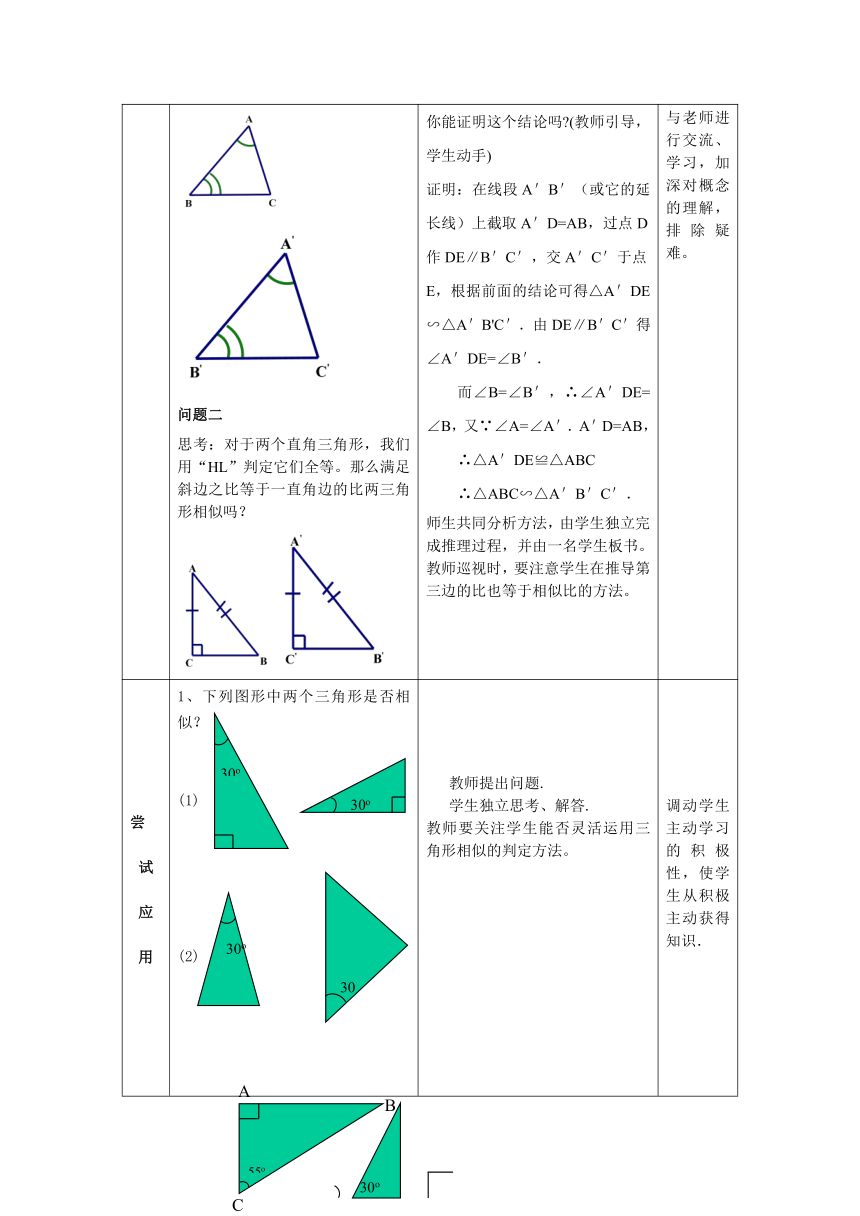
自主探究 问题一 1、与同伴合作,一人先画△ABC,另一人再画△A`B`C`,使得∠A= ∠A`, ∠B= ∠B`。2、比较你们所画的两个三角形, ∠C= ∠C`吗?3、度量边长,计算,,,你有什么发现?4、猜想:两个三角形至少有几个角对应相等,才能保证这两个三角形相似?5、已知: 如图,在△ABC和△A’B’C’中,∠A=∠A’,∠B=∠B’。求证:△ABC∽△A’B’C’。问题二 思考:对于两个直角三角形,我们用“HL”判定它们全等。那么满足斜边之比等于一直角边的比两三角形相似吗? 学生自己合作完成,教师巡视,并参与学生画图,指导和纠正错误的画法,并对画正确的学生,给予鼓励。学生先自己独立思考,然后由组长组织跟同组的同学一起讨论,交流结果。学生归纳,教师板书:三角形相似的判定方法3 如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似.你能证明这个结论吗 (教师引导,学生动手)证明:在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'.由DE∥B'C'得∠A'DE=∠B'.而∠B=∠B',∴∠A'DE=∠B,又∵∠A=∠A'.A'D=AB,∴△A'DE≌△ABC∴△ABC∽△A'B'C'.师生共同分析方法,由学生独立完成推理过程,并由一名学生板书。教师巡视时,要注意学生在推导第三边的比也等于相似比的方法。 从旧知识中发现新问题通过问题,使学生与学生,学生与老师进行交流、学习,加深对概念的理解,排除疑难。
尝试应用 1、下列图形中两个三角形是否相似?(1)(2)(3)2、判断题: ⑴所有的直角三角形都相似 . ⑵有一个锐角对应相等的两直角三角形相似. ⑶所有的等边三角形都相似. ⑷所有的等腰直角三角形都相似. ⑸顶角相等的两个等腰三角形相似. ⑹有一个角相等的两个等腰三角形相似. 3、如图,弦AB和CD相交于OO内一点P, 求证:PA PB = PC PD 教师提出问题.学生独立思考、解答.教师要关注学生能否灵活运用三角形相似的判定方法。学生完成后,小组讨论解决,対有疑难问题师生共同解决。 调动学生主动学习的积极性,使学生从积极主动获得知识.
补偿提高 已知如图直线BE、DC交于A , ∠E= ∠C求证:DA·AC=AB·AE 2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE. 学生练习时,教师巡视、辅导,了解学生的掌握情况.证明:∵ ∠E=∠C ∠1=∠2 ∴ △ABC ∽ △ADE ∴ AC :AE=AB :AD ∴ DA · AC=AB · AE小组讨论解决注意格式的规范性 学生在讨论中能否发表自己的见解,倾听他人的意见,并从中获益。
小结与作业 小结:通过这节课的学习,你有哪些收获?作业:1.教材P48练习1.2,2.下列说法是否正确,并说明理由.(1)有一个锐角相等的两直角三角形是相似三角形;(2)有一个角相等的两等腰三角形是相似三角形.2.已知:如图,△ABC 的高AD、BE交于点F.求证:. 教师提出问题.学生独立回答,教师在学生总结后,进行补充. 并根据学生的回答,结合结构图总结本节知识.教师布置作业,动员分层要求。学生按要求课外完成.学生通过课后作业巩固本节知识. 使学生能回顾、总结、梳理所学知识.
教后反思
五、设计思路
本本节课主要是探究相似三角形的判定方法3,由于上两节课已经学习了探究两个三角形相似的判定引例﹑判定方法1﹑判定方法2,因此本课教学力求使探究途径多元化,把学生利用刻度尺、量角器等作图工具作静态探究与应用“几何画板”等计算机软件作动态探究有机结合起来,让学生充分感受探究的全面性,丰富探究的内涵。协同式小组合作学习的开展不仅提高了数学实验的效率,而且培养了学生的合作能力。
30o
30o
30o
30o
30o
A
C
B
55o
O
D
P
C
B
A
D
E
A
B
C
1
2
蒋良金
一、教学目标
知识与技能
初步掌握“两角对应相等,两个三角形相似”的判定方法.
过程与方法
能够运用三角形相似的条件解决简单的问题.
情感态度与价值观
经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
二、重点难点
重点
掌握判定方法,会运用判定方法判定两个三角形相似.
难点
会准确的运用两个三角形相似的条件来判定三角形是否相似.
四、教学过程设计
教学环节 问 题 设 计 师 生 活 动 备注
情境创设 观察两副三角板,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小不同,它们相似吗? 创设问题情境,引起学生学习的兴趣.
自主探究 问题一 1、与同伴合作,一人先画△ABC,另一人再画△A`B`C`,使得∠A= ∠A`, ∠B= ∠B`。2、比较你们所画的两个三角形, ∠C= ∠C`吗?3、度量边长,计算,,,你有什么发现?4、猜想:两个三角形至少有几个角对应相等,才能保证这两个三角形相似?5、已知: 如图,在△ABC和△A’B’C’中,∠A=∠A’,∠B=∠B’。求证:△ABC∽△A’B’C’。问题二 思考:对于两个直角三角形,我们用“HL”判定它们全等。那么满足斜边之比等于一直角边的比两三角形相似吗? 学生自己合作完成,教师巡视,并参与学生画图,指导和纠正错误的画法,并对画正确的学生,给予鼓励。学生先自己独立思考,然后由组长组织跟同组的同学一起讨论,交流结果。学生归纳,教师板书:三角形相似的判定方法3 如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似.你能证明这个结论吗 (教师引导,学生动手)证明:在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'.由DE∥B'C'得∠A'DE=∠B'.而∠B=∠B',∴∠A'DE=∠B,又∵∠A=∠A'.A'D=AB,∴△A'DE≌△ABC∴△ABC∽△A'B'C'.师生共同分析方法,由学生独立完成推理过程,并由一名学生板书。教师巡视时,要注意学生在推导第三边的比也等于相似比的方法。 从旧知识中发现新问题通过问题,使学生与学生,学生与老师进行交流、学习,加深对概念的理解,排除疑难。
尝试应用 1、下列图形中两个三角形是否相似?(1)(2)(3)2、判断题: ⑴所有的直角三角形都相似 . ⑵有一个锐角对应相等的两直角三角形相似. ⑶所有的等边三角形都相似. ⑷所有的等腰直角三角形都相似. ⑸顶角相等的两个等腰三角形相似. ⑹有一个角相等的两个等腰三角形相似. 3、如图,弦AB和CD相交于OO内一点P, 求证:PA PB = PC PD 教师提出问题.学生独立思考、解答.教师要关注学生能否灵活运用三角形相似的判定方法。学生完成后,小组讨论解决,対有疑难问题师生共同解决。 调动学生主动学习的积极性,使学生从积极主动获得知识.
补偿提高 已知如图直线BE、DC交于A , ∠E= ∠C求证:DA·AC=AB·AE 2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE. 学生练习时,教师巡视、辅导,了解学生的掌握情况.证明:∵ ∠E=∠C ∠1=∠2 ∴ △ABC ∽ △ADE ∴ AC :AE=AB :AD ∴ DA · AC=AB · AE小组讨论解决注意格式的规范性 学生在讨论中能否发表自己的见解,倾听他人的意见,并从中获益。
小结与作业 小结:通过这节课的学习,你有哪些收获?作业:1.教材P48练习1.2,2.下列说法是否正确,并说明理由.(1)有一个锐角相等的两直角三角形是相似三角形;(2)有一个角相等的两等腰三角形是相似三角形.2.已知:如图,△ABC 的高AD、BE交于点F.求证:. 教师提出问题.学生独立回答,教师在学生总结后,进行补充. 并根据学生的回答,结合结构图总结本节知识.教师布置作业,动员分层要求。学生按要求课外完成.学生通过课后作业巩固本节知识. 使学生能回顾、总结、梳理所学知识.
教后反思
五、设计思路
本本节课主要是探究相似三角形的判定方法3,由于上两节课已经学习了探究两个三角形相似的判定引例﹑判定方法1﹑判定方法2,因此本课教学力求使探究途径多元化,把学生利用刻度尺、量角器等作图工具作静态探究与应用“几何画板”等计算机软件作动态探究有机结合起来,让学生充分感受探究的全面性,丰富探究的内涵。协同式小组合作学习的开展不仅提高了数学实验的效率,而且培养了学生的合作能力。
30o
30o
30o
30o
30o
A
C
B
55o
O
D
P
C
B
A
D
E
A
B
C
1
2
