沪科版数学八年级上册第13章 三角形中的边角关系、命题与证明达标测试卷 含答案
文档属性
| 名称 | 沪科版数学八年级上册第13章 三角形中的边角关系、命题与证明达标测试卷 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 13:52:11 | ||
图片预览



文档简介
第13章达标测试卷
一、选择题(每题3分,共30分)
1.下列语句中,不是命题的是( )
A.所有的平角都相等
B.锐角小于90°
C.两点确定一条直线
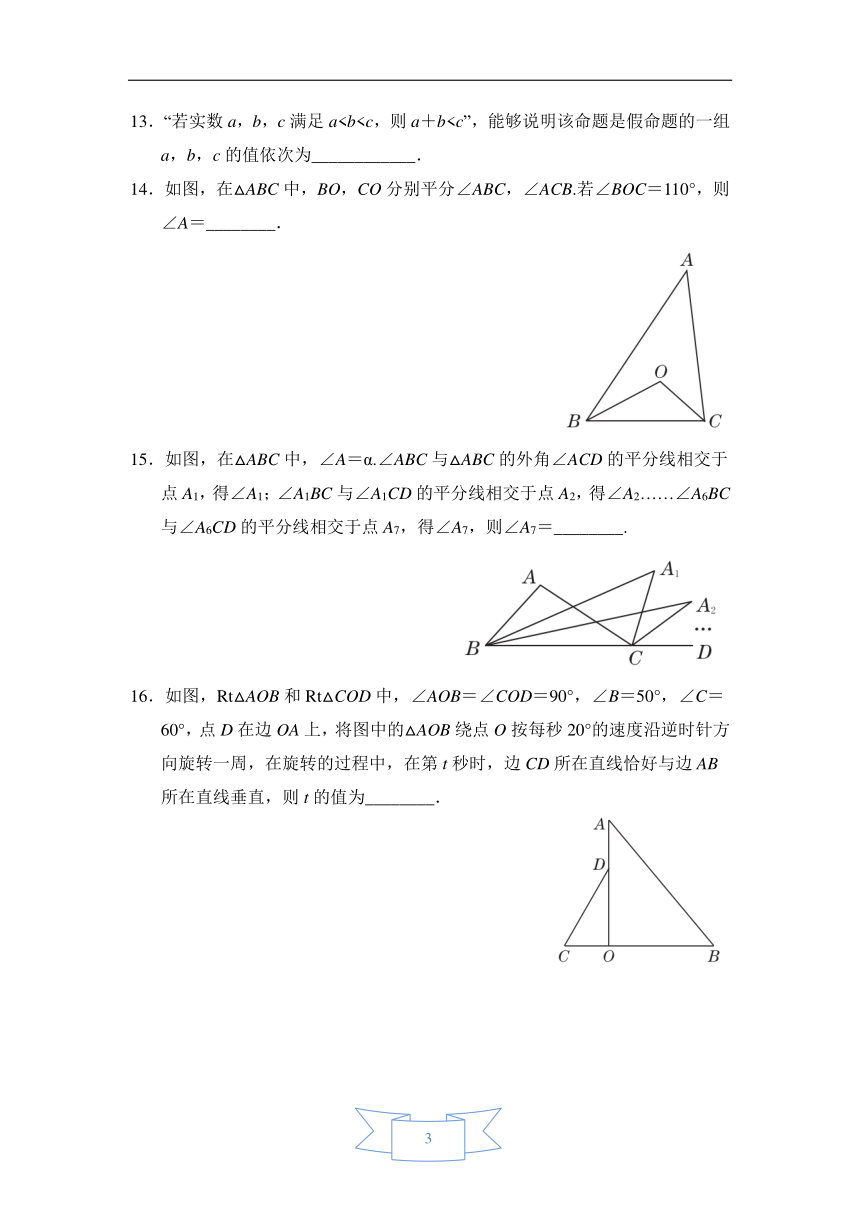
D.过一点作已知直线的平行线
2.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.①②
B.②④
C.②③
D.③④
3.图中能表示△ABC的BC边上的高的是( )
4.下列长度的三条线段能组成三角形的是( )
A.1,2,3
B.1,1.5,3
C.3,4,8
D.4,5,6
5.若三角形三个内角的度数的比为1?2?3,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.等腰直角三角形
6.下列命题:①三角形的三个内角中最多有一个钝角;②三角形的三个内角中至少有两个锐角;③有两个内角分别为50°和20°的三角形一定是钝角三角形;④直角三角形中两锐角之和为90°.其中是真命题的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,∠A=40°,点D为AB延长线上一点,且∠CBD=120°,则∠C的度数为( )
A.40°
B.60°
C.80°
D.100°
8.若线段2a+1,a,a+3能构成一个三角形,则a的范围是( )
A.a>0
B.a>1
C.a>2
D.1<a<3
9.如图,在△ABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD与BE交于F,则∠AFB的度数是( )
A.126°
B.120°
C.116°
D.110°
10.如图,在△ABC中,点D,E,F分别在三边上,点E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是( )
A.25
B.30
C.35
D.40
二、填空题(每题3分,共18分)
11.一个三角形的两边长分别是3和8,周长是偶数,那么第三边边长是________.
12.“直角三角形有两个角是锐角”的逆命题是______________________________,这个逆命题是一个________命题(填“真”或“假”).
13.“若实数a,b,c满足a14.如图,在△ABC中,BO,CO分别平分∠ABC,∠ACB.若∠BOC=110°,则∠A=________.
15.如图,在△ABC中,∠A=α.∠ABC与△ABC的外角∠ACD的平分线相交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2……∠A6BC与∠A6CD的平分线相交于点A7,得∠A7,则∠A7=________.
16.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD所在直线恰好与边AB所在直线垂直,则t的值为________.
三、解答题(17,18题每题6分,其余每题10分,共52分)
17.在△ABC中,∠A+∠B=∠C,∠B=2∠A.
(1)求∠A,∠B,∠C的度数;
(2)△ABC按边分类,属于什么三角形?△ABC按角分类,属于什么三角形?
18.如图,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
19.有一块三角形优良品种试验基地,如图,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制订出两种以上的划分方案以供选择(画图说明).
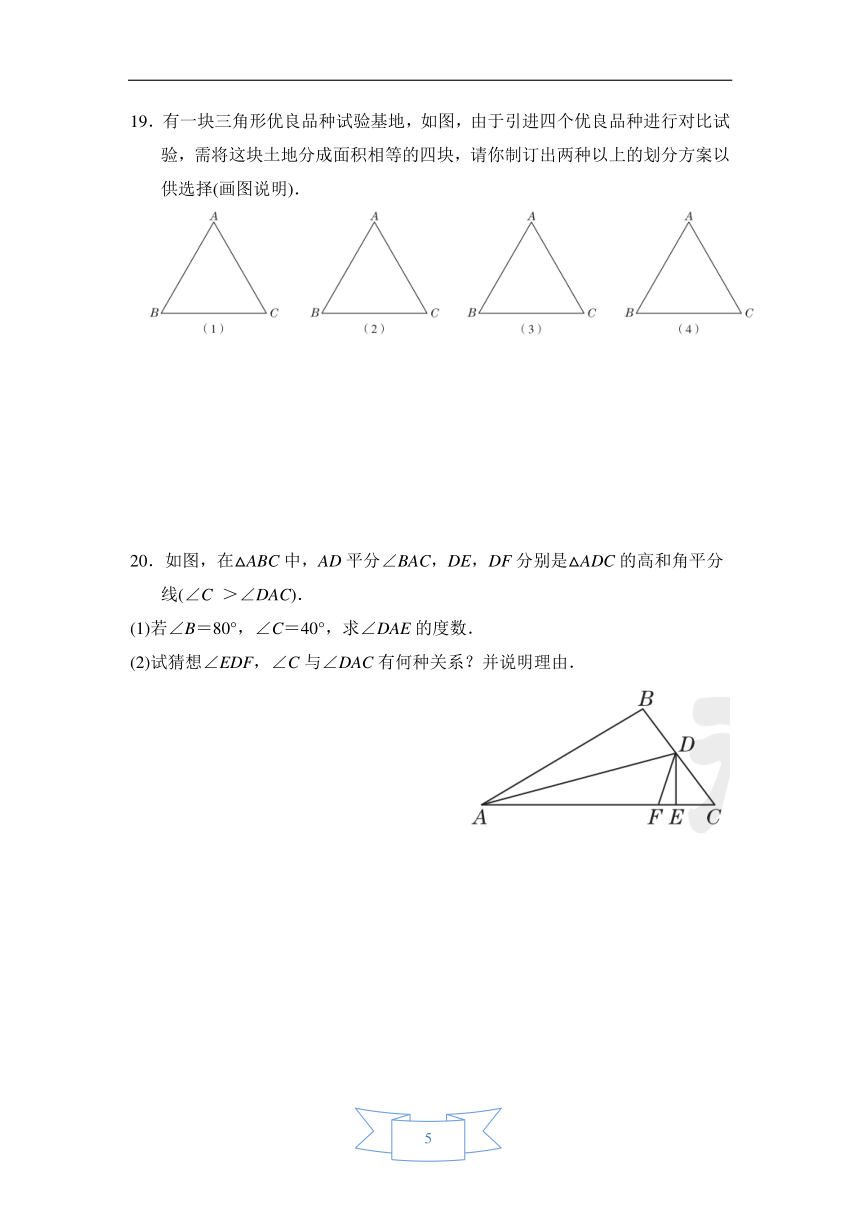
20.如图,在△ABC中,AD平分∠BAC,DE,DF分别是△ADC的高和角平分线(∠C
>∠DAC).
(1)若∠B=80°,∠C=40°,求∠DAE的度数.
(2)试猜想∠EDF,∠C与∠DAC有何种关系?并说明理由.
21.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,求∠BED的度数.
(2)作△BED中BD边上的高,垂足为F.
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
22.已知∠MON=40°,OE平分∠MON,点A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O重合),连接AC,交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则:①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
答案
一、1.D 2.B 3.D 4.D
5.C 点拨:利用方程思想求解,设三个内角的度数分别为x,2x,3x,则x+2x+3x=180°,解得x=30°.
所以3x=90°.
所以这个三角形是直角三角形.
6.D
7.C 点拨:∵∠CBD是△ABC的外角,∴∠CBD=∠C+∠A.
又∵∠A=40°,∠CBD=120°,
∴∠C=∠CBD-∠A=120°-40°=80°.
8.B
9.A 点拨:在△ABC中,∠CAB=52°,∠ABC=74°,∴∠ACB=180°-∠CAB-∠ABC=180°-52°-74°=54°.∵AD⊥BC,∴∠ADC=90°,∴∠DAE=90°-∠ACB=90°-54°=36°.又∵BE⊥AC,
∴∠AEB=90°,
∴∠AFB=∠DAE+∠AEB=36°+90°=126°.
10.B 点拨:在△BDG和△CDG中,由BD=2DC,知S△BDG=2S△GDC,因此S△GDC=4,同理S△AGE=S△GEC=3,所以S△BEC=S△BGD+S△GDC+S△GEC=8+4+3=15,所以△ABC的面积=2S△BEC=30.故选B.
二、11.7或9
12.有两个角是锐角的三角形是直角三角形;假
13.2,3,4(答案不唯一)
14.40° 15. 16.1或10
三、17.解:(1)因为∠A+∠B+∠C=180°,而∠A+∠B=∠C,所以2∠C=180°,所以∠C=90°.所以∠A+∠B=90°,而∠B=2∠A,所以3∠A=90°,所以∠A=30°,∠B=2∠A=60°.
(2)△ABC按边分类属于不等边三角形.按角分类属于直角三角形.
18.解:∵∠1=∠3+∠C,∠1=100°,∠C=80°,
∴∠3=20°.
∵∠2=∠3,∴∠2=10°.
∴∠ABC=180°-100°-10°=70°.
∵BE平分∠ABC,
∴∠ABE=35°.
∴∠4=∠2+∠ABE=45°.
19.解:答案不唯一,如图所示.
(方案一)如图(1),在BC上取点D,E,F,使BD=DE=EF=FC,连接AD,AE,AF;
(方案二)如图(2),分别取AB,BC,CA的中点D,E,F,连接DE,EF,FD;
(方案三)如图(3),分别取BC的中点D,CD的中点E,AB的中点F,连接AD,AE,DF;
(方案四)如图(4),分别取BC的中点D,AB的中点E,AC的中点F,连接AD,DE,DF.
20.解:(1)∵在△ABC中,∠B=80°,∠C=40°,
∴∠BAC=180°-80°-40°=60°.
∵AD平分∠BAC,
∴∠DAE=∠BAE=30°.
(2)∠EDF=(∠C-∠DAC).
理由如下:
在△DAC中,∵∠ADC+∠DAC+∠C=180°,
∴∠ADC=180°-∠DAC-∠C.
∵DF平分∠ADC,
∴∠CDF=∠ADC=(180°-∠DAC-∠C).
∵DE是△DAC的高,
∴∠CDE=90°-∠C,
∴∠EDF=∠CDF-∠CDE=(180°-∠DAC-∠C)-(90°-∠C)=(∠C-∠DAC).
21.解:(1)∵∠ABE=15°,∠BAD=40°,∴∠BED=∠ABE+∠BAD=15°+40°=55°.
(2)如图.
(3)∵AD为△ABC的中线,BE为△ABD的中线,∴S△ABD=S△ABC,S△BDE=S△ABD,∴S△BDE=×S△ABC=S△ABC.∵△ABC的面积为40,∴S△BDE=×40=10.
∵BD=5,∴×5·EF=10,解得EF=4,即
△BDE中BD边上的高为4.
22.解:(1)①20° ②120;60
(2)存在.①当点D在线段OB上时,若∠BAD=∠ABD,则x=20.若∠BAD=∠BDA,则x=35.若∠ADB=∠ABD,则x=50.
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20或35或50或125.
一、选择题(每题3分,共30分)
1.下列语句中,不是命题的是( )
A.所有的平角都相等
B.锐角小于90°
C.两点确定一条直线
D.过一点作已知直线的平行线
2.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
A.①②
B.②④
C.②③
D.③④
3.图中能表示△ABC的BC边上的高的是( )
4.下列长度的三条线段能组成三角形的是( )
A.1,2,3
B.1,1.5,3
C.3,4,8
D.4,5,6
5.若三角形三个内角的度数的比为1?2?3,则这个三角形是( )
A.钝角三角形
B.锐角三角形
C.直角三角形
D.等腰直角三角形
6.下列命题:①三角形的三个内角中最多有一个钝角;②三角形的三个内角中至少有两个锐角;③有两个内角分别为50°和20°的三角形一定是钝角三角形;④直角三角形中两锐角之和为90°.其中是真命题的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,∠A=40°,点D为AB延长线上一点,且∠CBD=120°,则∠C的度数为( )
A.40°
B.60°
C.80°
D.100°
8.若线段2a+1,a,a+3能构成一个三角形,则a的范围是( )
A.a>0
B.a>1
C.a>2
D.1<a<3
9.如图,在△ABC中,∠CAB=52°,∠ABC=74°,AD⊥BC,BE⊥AC,AD与BE交于F,则∠AFB的度数是( )
A.126°
B.120°
C.116°
D.110°
10.如图,在△ABC中,点D,E,F分别在三边上,点E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是( )
A.25
B.30
C.35
D.40
二、填空题(每题3分,共18分)
11.一个三角形的两边长分别是3和8,周长是偶数,那么第三边边长是________.
12.“直角三角形有两个角是锐角”的逆命题是______________________________,这个逆命题是一个________命题(填“真”或“假”).
13.“若实数a,b,c满足a
15.如图,在△ABC中,∠A=α.∠ABC与△ABC的外角∠ACD的平分线相交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2……∠A6BC与∠A6CD的平分线相交于点A7,得∠A7,则∠A7=________.
16.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD所在直线恰好与边AB所在直线垂直,则t的值为________.
三、解答题(17,18题每题6分,其余每题10分,共52分)
17.在△ABC中,∠A+∠B=∠C,∠B=2∠A.
(1)求∠A,∠B,∠C的度数;
(2)△ABC按边分类,属于什么三角形?△ABC按角分类,属于什么三角形?
18.如图,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
19.有一块三角形优良品种试验基地,如图,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制订出两种以上的划分方案以供选择(画图说明).
20.如图,在△ABC中,AD平分∠BAC,DE,DF分别是△ADC的高和角平分线(∠C
>∠DAC).
(1)若∠B=80°,∠C=40°,求∠DAE的度数.
(2)试猜想∠EDF,∠C与∠DAC有何种关系?并说明理由.
21.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,求∠BED的度数.
(2)作△BED中BD边上的高,垂足为F.
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
22.已知∠MON=40°,OE平分∠MON,点A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O重合),连接AC,交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则:①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
答案
一、1.D 2.B 3.D 4.D
5.C 点拨:利用方程思想求解,设三个内角的度数分别为x,2x,3x,则x+2x+3x=180°,解得x=30°.
所以3x=90°.
所以这个三角形是直角三角形.
6.D
7.C 点拨:∵∠CBD是△ABC的外角,∴∠CBD=∠C+∠A.
又∵∠A=40°,∠CBD=120°,
∴∠C=∠CBD-∠A=120°-40°=80°.
8.B
9.A 点拨:在△ABC中,∠CAB=52°,∠ABC=74°,∴∠ACB=180°-∠CAB-∠ABC=180°-52°-74°=54°.∵AD⊥BC,∴∠ADC=90°,∴∠DAE=90°-∠ACB=90°-54°=36°.又∵BE⊥AC,
∴∠AEB=90°,
∴∠AFB=∠DAE+∠AEB=36°+90°=126°.
10.B 点拨:在△BDG和△CDG中,由BD=2DC,知S△BDG=2S△GDC,因此S△GDC=4,同理S△AGE=S△GEC=3,所以S△BEC=S△BGD+S△GDC+S△GEC=8+4+3=15,所以△ABC的面积=2S△BEC=30.故选B.
二、11.7或9
12.有两个角是锐角的三角形是直角三角形;假
13.2,3,4(答案不唯一)
14.40° 15. 16.1或10
三、17.解:(1)因为∠A+∠B+∠C=180°,而∠A+∠B=∠C,所以2∠C=180°,所以∠C=90°.所以∠A+∠B=90°,而∠B=2∠A,所以3∠A=90°,所以∠A=30°,∠B=2∠A=60°.
(2)△ABC按边分类属于不等边三角形.按角分类属于直角三角形.
18.解:∵∠1=∠3+∠C,∠1=100°,∠C=80°,
∴∠3=20°.
∵∠2=∠3,∴∠2=10°.
∴∠ABC=180°-100°-10°=70°.
∵BE平分∠ABC,
∴∠ABE=35°.
∴∠4=∠2+∠ABE=45°.
19.解:答案不唯一,如图所示.
(方案一)如图(1),在BC上取点D,E,F,使BD=DE=EF=FC,连接AD,AE,AF;
(方案二)如图(2),分别取AB,BC,CA的中点D,E,F,连接DE,EF,FD;
(方案三)如图(3),分别取BC的中点D,CD的中点E,AB的中点F,连接AD,AE,DF;
(方案四)如图(4),分别取BC的中点D,AB的中点E,AC的中点F,连接AD,DE,DF.
20.解:(1)∵在△ABC中,∠B=80°,∠C=40°,
∴∠BAC=180°-80°-40°=60°.
∵AD平分∠BAC,
∴∠DAE=∠BAE=30°.
(2)∠EDF=(∠C-∠DAC).
理由如下:
在△DAC中,∵∠ADC+∠DAC+∠C=180°,
∴∠ADC=180°-∠DAC-∠C.
∵DF平分∠ADC,
∴∠CDF=∠ADC=(180°-∠DAC-∠C).
∵DE是△DAC的高,
∴∠CDE=90°-∠C,
∴∠EDF=∠CDF-∠CDE=(180°-∠DAC-∠C)-(90°-∠C)=(∠C-∠DAC).
21.解:(1)∵∠ABE=15°,∠BAD=40°,∴∠BED=∠ABE+∠BAD=15°+40°=55°.
(2)如图.
(3)∵AD为△ABC的中线,BE为△ABD的中线,∴S△ABD=S△ABC,S△BDE=S△ABD,∴S△BDE=×S△ABC=S△ABC.∵△ABC的面积为40,∴S△BDE=×40=10.
∵BD=5,∴×5·EF=10,解得EF=4,即
△BDE中BD边上的高为4.
22.解:(1)①20° ②120;60
(2)存在.①当点D在线段OB上时,若∠BAD=∠ABD,则x=20.若∠BAD=∠BDA,则x=35.若∠ADB=∠ABD,则x=50.
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20或35或50或125.
