华师大版数学八年级上册第13章全等三角形达标测试卷 含答案
文档属性
| 名称 | 华师大版数学八年级上册第13章全等三角形达标测试卷 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-02 13:52:41 | ||
图片预览


文档简介
第13章达标测试卷
一、选择题(每题3分,共30分)
1.下列命题是假命题的是( )
A.两点确定一条直线
B.角平分线上的点到角两边的距离相等
C.有一个角等于60°的等腰三角形是等边三角形
D.角的边越长,角就越大
2.如图,已知AC=DB,AB=DC,你认为证明△ABC≌△DCB应该用( )
A.“边边边”
B.“边角边”
C.“角边角”
D.“角角边”
3.如图,已知△ABC的六个元素,图(1)(2)(3)中的三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.(2)
B.(3)
C.(1)和(2)
D.(2)和(3)
4.“已知等腰三角形的底边和底边上的高,用尺规作图求作等腰三角形”里用到的基本作图是( )
A.作一条线段等于已知线段,作已知线段的垂直平分线
B.作已知角的平分线
C.过直线外一点作已知直线的垂线
D.作一个角等于已知角
5.已知△ABC≌△A′B′C′,且△ABC的周长为20,AB=8,BC=5,则A′C′等于( )
A.5
B.6
C.7
D.8
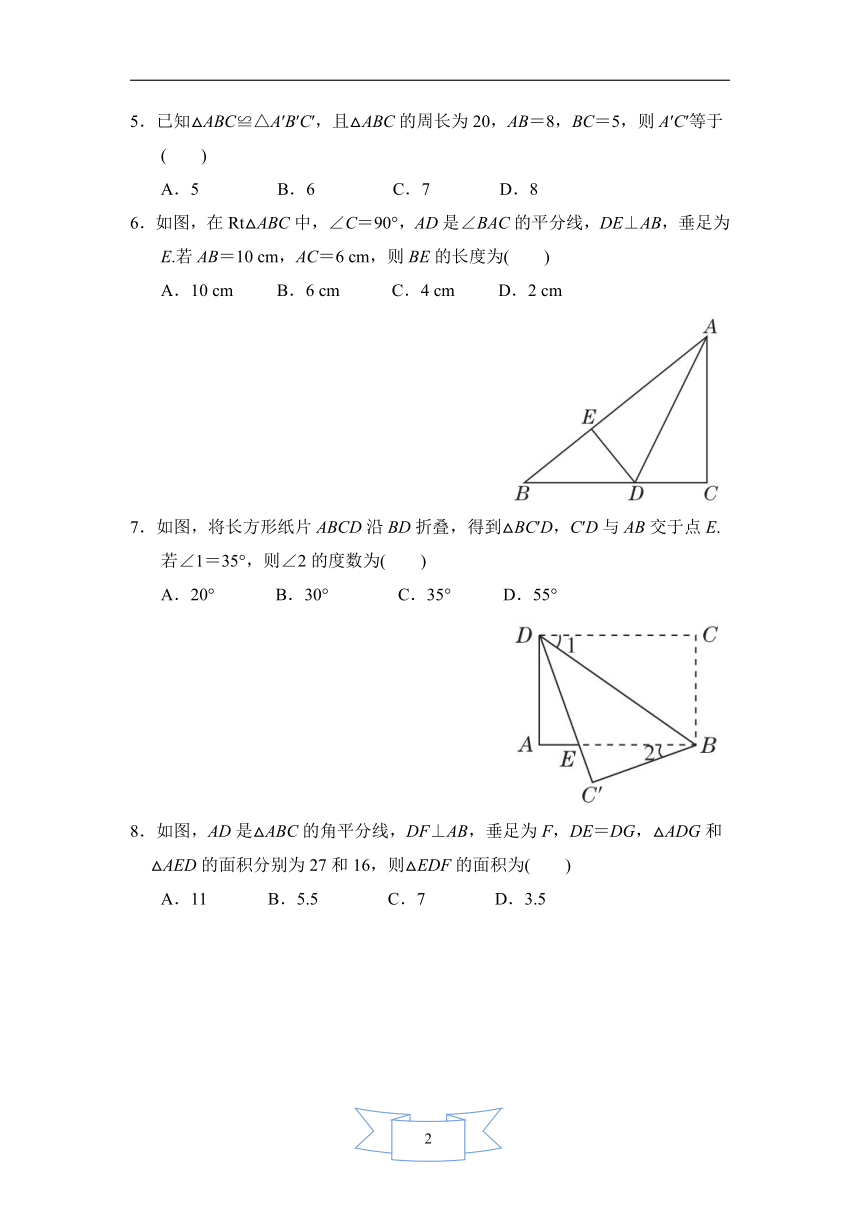
6.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.若AB=10
cm,AC=6
cm,则BE的长度为( )
A.10
cm
B.6
cm
C.4
cm
D.2
cm
7.如图,将长方形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20°
B.30°
C.35°
D.55°
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为27和16,则△EDF的面积为( )
A.11
B.5.5
C.7
D.3.5
9.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3
B.4
C.5
D.6
10.如图,将含有30°角的直角三角尺ABC绕直角顶点A逆时针旋转到△ADE的位置,使B点的对应点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ABD为等边三角形.其中正确的是( )
A.①②③
B.①②④
C.②③④
D.①②③④
二、填空题(每题3分,共30分)
11.把命题“等边对等角”的逆命题写成“如果……,那么……”的形式为________________________________________________________________________.
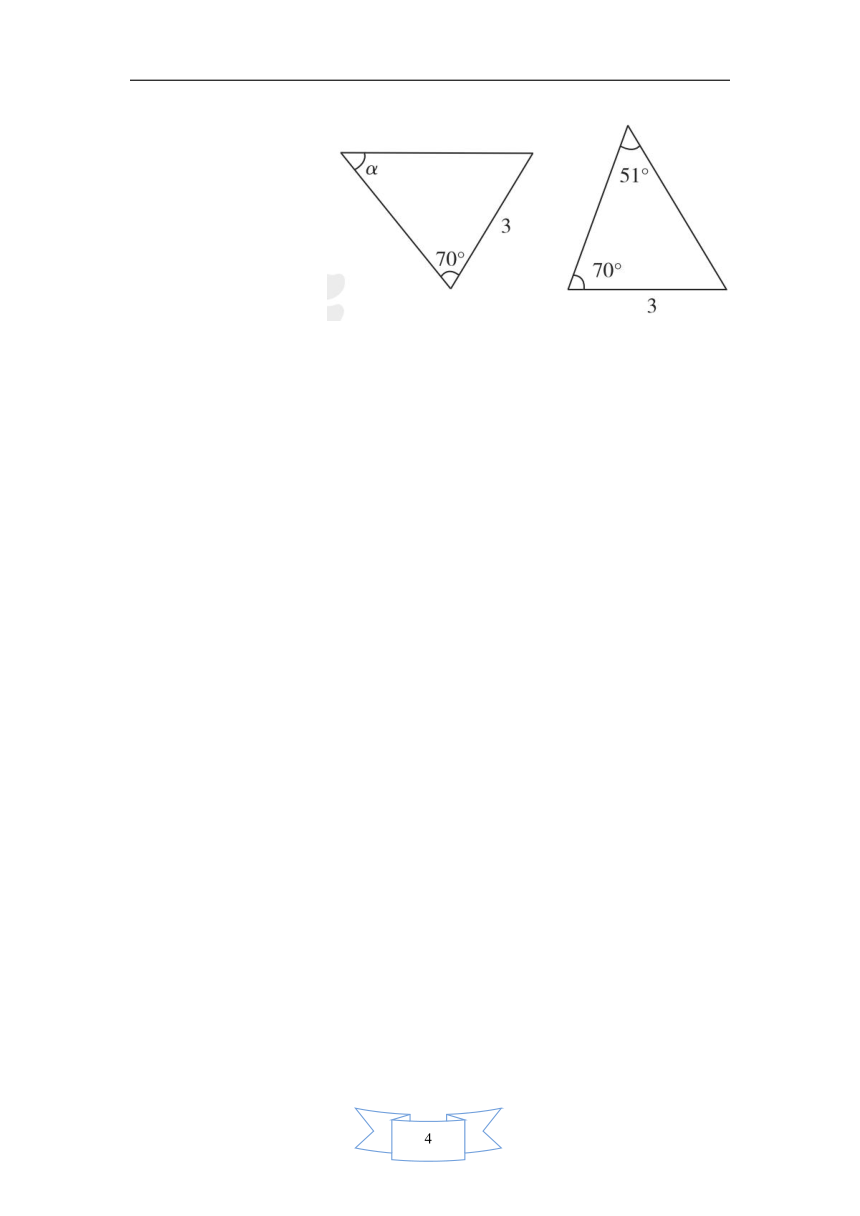
12.如图,两个三角形全等,根据图中所给的条件可知∠α=________.
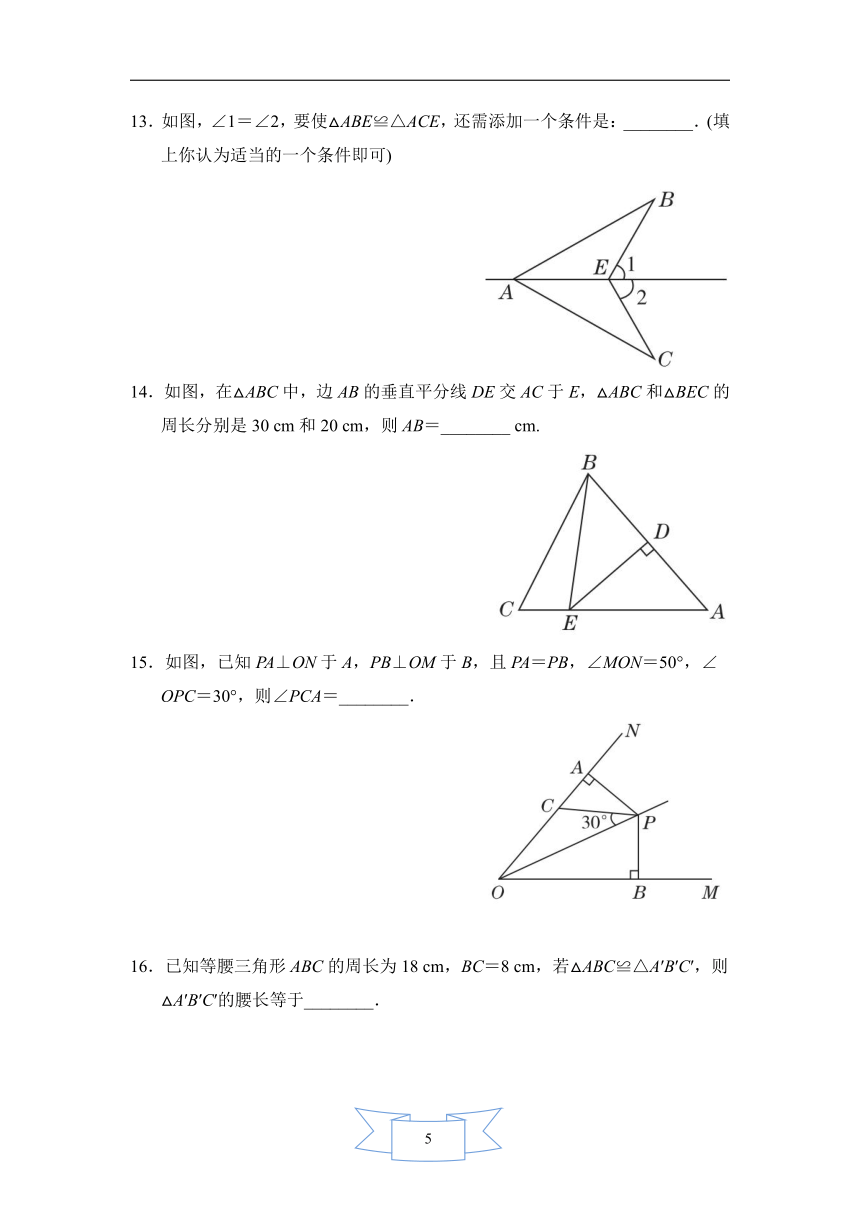
13.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是:________.(填上你认为适当的一个条件即可)
14.如图,在△ABC中,边AB的垂直平分线DE交AC于E,△ABC和△BEC的周长分别是30
cm和20
cm,则AB=________
cm.
15.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=________.
16.已知等腰三角形ABC的周长为18
cm,BC=8
cm,若△ABC≌△A′B′C′,则△A′B′C′的腰长等于________.
17.如图,在四边形ABCD中,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC=________.
18.如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为________.
19.如图,AB=12
m,CA⊥AB于点A,DB⊥AB于点B,且AC=4
m.点P从点B开始以1
m/min的速度向点A运动;点Q从点B开始以2
m/min的速度向点D运动.P,Q两点同时出发,运动________后,△CAP≌△PBQ.
20.如图,在△ABC中,BC的垂直平分线与∠BAC的邻补角的平分线相交于点D,DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CA-AB=2AE;③∠BDC+∠FAE=180°;④∠BAC=90°.其中正确的有____________.(填序号)
三、解答题(21,22题每题6分,23,24题每题8分,25,26题每题10分,27题12分,共60分)
21.如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).
22.如图,在平行四边形ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连结EF,与对角线AC交于点O.
求证:OE=OF.
23.如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
24.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,BD=DF.
求证:(1)CF=EB;(2)AB=AF+2EB.
25.如图,A,B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发在河岸上画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使E,C,A三点在同一直线上,则DE的长就是A,B之间的距离,请你说明道理.
26.如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
27.如图a,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图b,线段CF,BD所在直线的位置关系为________,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图c,①中的结论是否仍然成立,并说明理由.
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
答案
一、1.D 2.A 3.D 4.A 5.C 6.C
7.A 点拨:在Rt△DBC中,∠DCB=90°,∠1=35°,∴∠DBC=55°.
由折叠的性质可知△DBC≌△DBC′,
∴∠DBC′=∠DBC=55°.
又∵DC∥AB,∴∠DBA=∠1=35°.
∴∠2=∠DBC′-∠DBA=20°.故选A.
8.B
9.B 点拨:假设AB=AC=4,BC=6,如图,当CD=AC=4时,直线AD符合要求.当BE=AB=4时,直线AE符合要求.作线段AC的垂直平分线交BC于点F,则AF=FC,直线AF符合要求.作线段AB的垂直平分线交BC于点G,则AG=BG,直线AG符合要求.∴这样的直线最多可以画4条.故选B.
10.B
二、11.如果一个三角形有两个角相等,那么这两个角所对的边相等
12.51°
13.∠B=∠C(答案不唯一)
14.10 15.55° 16.8
cm或5
cm
17.80° 18.4 19.4
min
20.①②③
三、21.解:如图.
22.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵BE=DF,
∴AB+BE=CD+DF,即AE=CF.
∵AB∥CD,∴AE∥CF.
∴∠E=∠F.
又∵∠AOE=∠COF,
∴△AOE≌△COF.∴OE=OF.
23.解:(1)∵DE垂直平分AC,
∴AE=CE,∴∠ECD=∠A=36°.
(2)∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°.
又∵∠ECD=36°,
∴∠ECB=72°-36°=36°.
∴∠BEC=180°-∠ABC-∠ECB=180°-72°-36°=72°.
∴∠B=∠BEC,∴BC=CE=5.
24.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DE=DC,∠C=∠DEB=90°.
又∵BD=DF,
∴Rt△CDF≌Rt△EDB(H.L.),
∴CF=EB.
(2)由(1)可知DE=DC,
又∵AD=AD,∠C=∠AED=90°,
∴Rt△ADC≌Rt△ADE(H.L.),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
点拨:(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得CD=DE.进而证得Rt△CDF≌Rt△EDB,得CF=EB.(2)利用角平分线的性质证明Rt△ADC≌Rt△ADE,得AC=AE,再将线段AB进行转化.
25.解:∵E,C,A三点在同一直线上,B,C,D三点在同一直线上,∴∠ACB=∠ECD.
∵DE∥AB,∴∠A=∠E.
在△ABC与△EDC中,
∴△ABC≌△EDC(A.A.S.).
∴AB=DE.
26.(1)证明:∵ED⊥AC,FB⊥AC,∴∠DEG=∠BFE=90°.
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(H.L.).
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(A.A.S.).
∴FG=EG,即BD平分EF.
(2)解:BD平分EF的结论仍然成立.
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE.
∵ED⊥AC,FB⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(H.L.).
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(A.A.S.).
∴GF=GE,即BD平分EF,结论仍然成立.
点拨:本题综合考查了三角形全等的判定方法.(1)先利用H.L.判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用A.A.S.判定△BFG≌△DEG,从而得出FG=EG,即BD平分EF.(2)中结论仍然成立,证明过程同(1)类似.
27.解:(1)①CF⊥BD;CF=BD
②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BC(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,∴∠ACB=∠AGC=45°,∴△AGC是等腰直角三角形,∴AC=AG.
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
一、选择题(每题3分,共30分)
1.下列命题是假命题的是( )
A.两点确定一条直线
B.角平分线上的点到角两边的距离相等
C.有一个角等于60°的等腰三角形是等边三角形
D.角的边越长,角就越大
2.如图,已知AC=DB,AB=DC,你认为证明△ABC≌△DCB应该用( )
A.“边边边”
B.“边角边”
C.“角边角”
D.“角角边”
3.如图,已知△ABC的六个元素,图(1)(2)(3)中的三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.(2)
B.(3)
C.(1)和(2)
D.(2)和(3)
4.“已知等腰三角形的底边和底边上的高,用尺规作图求作等腰三角形”里用到的基本作图是( )
A.作一条线段等于已知线段,作已知线段的垂直平分线
B.作已知角的平分线
C.过直线外一点作已知直线的垂线
D.作一个角等于已知角
5.已知△ABC≌△A′B′C′,且△ABC的周长为20,AB=8,BC=5,则A′C′等于( )
A.5
B.6
C.7
D.8
6.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.若AB=10
cm,AC=6
cm,则BE的长度为( )
A.10
cm
B.6
cm
C.4
cm
D.2
cm
7.如图,将长方形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20°
B.30°
C.35°
D.55°
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为27和16,则△EDF的面积为( )
A.11
B.5.5
C.7
D.3.5
9.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3
B.4
C.5
D.6
10.如图,将含有30°角的直角三角尺ABC绕直角顶点A逆时针旋转到△ADE的位置,使B点的对应点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ABD为等边三角形.其中正确的是( )
A.①②③
B.①②④
C.②③④
D.①②③④
二、填空题(每题3分,共30分)
11.把命题“等边对等角”的逆命题写成“如果……,那么……”的形式为________________________________________________________________________.
12.如图,两个三角形全等,根据图中所给的条件可知∠α=________.
13.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是:________.(填上你认为适当的一个条件即可)
14.如图,在△ABC中,边AB的垂直平分线DE交AC于E,△ABC和△BEC的周长分别是30
cm和20
cm,则AB=________
cm.
15.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=________.
16.已知等腰三角形ABC的周长为18
cm,BC=8
cm,若△ABC≌△A′B′C′,则△A′B′C′的腰长等于________.
17.如图,在四边形ABCD中,∠ABC=∠DCB=70°,∠ABD=40°,AB=DC,则∠BAC=________.
18.如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为________.
19.如图,AB=12
m,CA⊥AB于点A,DB⊥AB于点B,且AC=4
m.点P从点B开始以1
m/min的速度向点A运动;点Q从点B开始以2
m/min的速度向点D运动.P,Q两点同时出发,运动________后,△CAP≌△PBQ.
20.如图,在△ABC中,BC的垂直平分线与∠BAC的邻补角的平分线相交于点D,DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CA-AB=2AE;③∠BDC+∠FAE=180°;④∠BAC=90°.其中正确的有____________.(填序号)
三、解答题(21,22题每题6分,23,24题每题8分,25,26题每题10分,27题12分,共60分)
21.如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).
22.如图,在平行四边形ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连结EF,与对角线AC交于点O.
求证:OE=OF.
23.如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
24.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,BD=DF.
求证:(1)CF=EB;(2)AB=AF+2EB.
25.如图,A,B两建筑物位于河的两岸,要测得它们之间的距离,可以从B点出发在河岸上画一条射线BF,在BF上截取BC=CD,过点D作DE∥AB,使E,C,A三点在同一直线上,则DE的长就是A,B之间的距离,请你说明道理.
26.如图①,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)若BD与EF交于点G,求证:BD平分EF;
(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
27.如图a,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图b,线段CF,BD所在直线的位置关系为________,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图c,①中的结论是否仍然成立,并说明理由.
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合)?并说明理由.
答案
一、1.D 2.A 3.D 4.A 5.C 6.C
7.A 点拨:在Rt△DBC中,∠DCB=90°,∠1=35°,∴∠DBC=55°.
由折叠的性质可知△DBC≌△DBC′,
∴∠DBC′=∠DBC=55°.
又∵DC∥AB,∴∠DBA=∠1=35°.
∴∠2=∠DBC′-∠DBA=20°.故选A.
8.B
9.B 点拨:假设AB=AC=4,BC=6,如图,当CD=AC=4时,直线AD符合要求.当BE=AB=4时,直线AE符合要求.作线段AC的垂直平分线交BC于点F,则AF=FC,直线AF符合要求.作线段AB的垂直平分线交BC于点G,则AG=BG,直线AG符合要求.∴这样的直线最多可以画4条.故选B.
10.B
二、11.如果一个三角形有两个角相等,那么这两个角所对的边相等
12.51°
13.∠B=∠C(答案不唯一)
14.10 15.55° 16.8
cm或5
cm
17.80° 18.4 19.4
min
20.①②③
三、21.解:如图.
22.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵BE=DF,
∴AB+BE=CD+DF,即AE=CF.
∵AB∥CD,∴AE∥CF.
∴∠E=∠F.
又∵∠AOE=∠COF,
∴△AOE≌△COF.∴OE=OF.
23.解:(1)∵DE垂直平分AC,
∴AE=CE,∴∠ECD=∠A=36°.
(2)∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°.
又∵∠ECD=36°,
∴∠ECB=72°-36°=36°.
∴∠BEC=180°-∠ABC-∠ECB=180°-72°-36°=72°.
∴∠B=∠BEC,∴BC=CE=5.
24.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,
∴DE=DC,∠C=∠DEB=90°.
又∵BD=DF,
∴Rt△CDF≌Rt△EDB(H.L.),
∴CF=EB.
(2)由(1)可知DE=DC,
又∵AD=AD,∠C=∠AED=90°,
∴Rt△ADC≌Rt△ADE(H.L.),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
点拨:(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得CD=DE.进而证得Rt△CDF≌Rt△EDB,得CF=EB.(2)利用角平分线的性质证明Rt△ADC≌Rt△ADE,得AC=AE,再将线段AB进行转化.
25.解:∵E,C,A三点在同一直线上,B,C,D三点在同一直线上,∴∠ACB=∠ECD.
∵DE∥AB,∴∠A=∠E.
在△ABC与△EDC中,
∴△ABC≌△EDC(A.A.S.).
∴AB=DE.
26.(1)证明:∵ED⊥AC,FB⊥AC,∴∠DEG=∠BFE=90°.
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(H.L.).
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(A.A.S.).
∴FG=EG,即BD平分EF.
(2)解:BD平分EF的结论仍然成立.
理由:∵AE=CF,
∴AE-EF=CF-EF,即AF=CE.
∵ED⊥AC,FB⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(H.L.).
∴BF=DE.
在△BFG和△DEG中,
∴△BFG≌△DEG(A.A.S.).
∴GF=GE,即BD平分EF,结论仍然成立.
点拨:本题综合考查了三角形全等的判定方法.(1)先利用H.L.判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用A.A.S.判定△BFG≌△DEG,从而得出FG=EG,即BD平分EF.(2)中结论仍然成立,证明过程同(1)类似.
27.解:(1)①CF⊥BD;CF=BD
②当点D在线段BC的延长线上时,①中的结论仍然成立.理由如下:由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BC(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,∴∠ACB=∠AGC=45°,∴△AGC是等腰直角三角形,∴AC=AG.
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
