人教八下数学教案18.2.2 菱形(第2课时)教案
文档属性
| 名称 | 人教八下数学教案18.2.2 菱形(第2课时)教案 |  | |
| 格式 | doc | ||
| 文件大小 | 49.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-03 12:36:15 | ||
图片预览

文档简介
菱形的判定
一、教学目标:
(1)知识目标:
经历菱形判定方法探究过程,掌握菱形三种判定方法 ,会根据菱形的三种判定方法判定一个四边形是菱形。
(2)能力目标:
1、经历利用菱形定义探究菱形其他判定方法的过程,培养学生的观察、推理的意识,发展学生的形象思维和逻辑推理能力。
2、根据菱形的判定进行简单的证明,培养学生逻辑推理能力和演绎能力。
(3)情感目标:
在探究菱形的判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心。
二、教学重点: 探索菱形判定定理的过程及应用
三、教学难点: 合理应用菱形的判定定理解决问题
四、学情分析:学生已掌握了平行四边形、矩形有关知识及菱形的定义和性质,经历过利用木条自己制作学具并进行探究的活动,对其探究方法有所了解。作为初二学生,他们的空间观念已初步建立,天生的好奇心成为孩子们学习的最好动力。经过培养我班学生具有了一定地主动探究的意识和习惯,对于自我展示有较强的渴望和一定的技能。学生学习的困难是利用所学知识对猜想和问题进行推理论证。
五、教法与学法:
1、教法
(1)创设问题情景,结合具体实例,让学生亲身经历数学知识发现和解决的过程,体验学习的快乐, 建立学习的信心。
(2)结合具体实例,让学生动脑自己归纳出结论
2、学法
观察讨论、自主探究、合作交流,猜想 验证。
六、教学资源:多媒体课件、可以转动的木条十字架、等腰三角形纸板(不等边)、三角板
七、教学过程:
(一)复习回归,导入新课
1、菱形的定义:一组邻边相等的平行四边形是菱形。
2、菱形的性质:(1)菱形的两组对边分别平行,四条边都相等;
(2) 菱形的两组对角分别相等,邻角互补;
(3)菱形的两条对角线互相平分;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
3、对称性:是轴对称图形,有两条对称轴。
4、菱形具有平行四边形的所有性质。
5、导入:
要判定一个四边形是菱形,除根据定义判定外,还有其它的判定方法吗?
(二)合作探究,自主归纳
1、学生自己制作的学具,一长一短两根木条,在它们的中点处固定一个小钉,做成一个可以转动的十字架,任意转动其中的一根木条,用笔和直尺画出木条四个端点的连线。
观察这个四边形总有什么特征?能证明你的发现吗?
设计意图:学生利用平行四边形的判定方法得出图形总是平行四边形。既为菱形的第二种判定方法的探究作好了知识上的铺垫,又巩固了平行四边形的判定方法,培养学生的观察能力和推理能力。
2、继续转动木条,观察什么时候围成的四边形变成菱形。
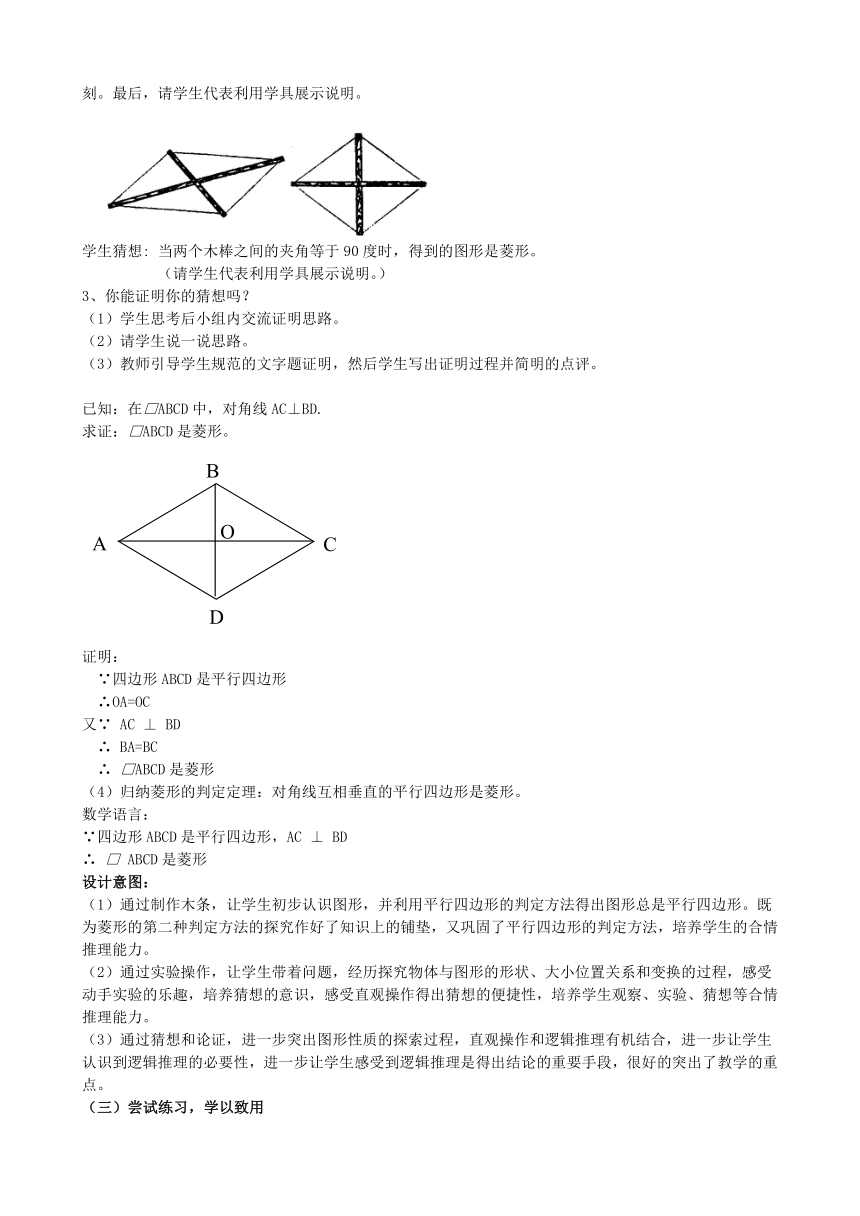
这时教师深入学生之中,引导学生观察,探究,深入思考。了解学生探究的过程,观察指导学生探究方法。得出结论,当两个木棒之间的夹角等于90度时,得到的图形是菱形。给学生以直观感受,印象深刻。最后,请学生代表利用学具展示说明。
学生猜想: 当两个木棒之间的夹角等于90度时,得到的图形是菱形。
(请学生代表利用学具展示说明。)
3、你能证明你的猜想吗?
(1)学生思考后小组内交流证明思路。
(2)请学生说一说思路。
(3)教师引导学生规范的文字题证明,然后学生写出证明过程并简明的点评。
已知:在□ABCD中,对角线AC⊥BD.
求证:□ABCD是菱形。
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵ AC ⊥ BD
∴ BA=BC
∴ □ABCD是菱形
(4)归纳菱形的判定定理:对角线互相垂直的平行四边形是菱形。
数学语言:
∵四边形ABCD是平行四边形,AC ⊥ BD
∴ □ ABCD是菱形
设计意图:
(1)通过制作木条,让学生初步认识图形,并利用平行四边形的判定方法得出图形总是平行四边形。既为菱形的第二种判定方法的探究作好了知识上的铺垫,又巩固了平行四边形的判定方法,培养学生的合情推理能力。
(2)通过实验操作,让学生带着问题,经历探究物体与图形的形状、大小位置关系和变换的过程,感受动手实验的乐趣,培养猜想的意识,感受直观操作得出猜想的便捷性,培养学生观察、实验、猜想等合情推理能力。
(3)通过猜想和论证,进一步突出图形性质的探索过程,直观操作和逻辑推理有机结合,进一步让学生认识到逻辑推理的必要性,进一步让学生感受到逻辑推理是得出结论的重要手段,很好的突出了教学的重点。
(三)尝试练习,学以致用
例 如图,如图,□ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3,求证:□ABCD是菱形。
1、学生充分思考后,交流不同的思路。教师引导学生选择恰当的方法。
2、教师指导学生完成规范证明。教师出示规范的板演,学生进行对照学习。
设计意图:根据已知条件明确思路、选择恰当的方法是问题解决的基本策略,学生经过独立思考、讨论交流、规范证明等过程,进一步培养推理论证、解决问题的能力。
(四)再次合作,探究新知
让学生拿出课前准备的两个全等的等腰三角形纸板(不等边),小组交流,开动脑筋,动手拼一拼,看一下可以拼出几种平行四边形。
1、问题解决:当两底边重合时拼出的四边形是什么图形?它的四条边有什么样的数量关系
2、思考与归纳:你能得到什么结论?
3、学生代表展示作品,并利用作品说明结论。 最后得出:四边相等的四边形是菱形。教师指导学生规范完成几何论证过程。
4、归纳菱形的判定定理:四边相等的四边形是菱形。
设计意图:这一探究活动贴近生活、轻松自然。学生利用平行四边形的判定和菱形的定义,演示说明自己的作品就是菱形,进一步培养了推理论证能力,体验了数学与生活的密切联系,产生了极大的成就感。
学生展示几何论证过程:
已知:在四边形ABCD中,AB=BC=CD=DA。
求证:四边形ABCD是菱形
证明:∵AD=BC AB=CD
∴四边形ABCD是平行四边形
又∵AB=AD
∴四边形ABCD是菱形
归纳菱形的判定定理:四条边都相等的四边形是菱形。
数学语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
(五)练习巩固
学生独立思考,教师点拨证明的思路。学生板演,教师点评。
设计意图:通过添加复习题上的一题,学生在做题之后,进一步掌握四边相等的四边形是菱形的这一判定方法。既巩固了三角形的中位线定理和矩形的性质,又达到了学以致用的目的,培养了学生的应用意识。
(六)随堂练习
一个平行四边形的一条边长是9,两条对角线的长分别是12和
6,这是一个特殊的平行四边形吗?为什么?求出它的面积。
设计意图:进一步培养根据已知条件和对图形的观察进行合情推理,选择合适的判定方法进行推理论证的能力。
(七)总结和反思
1、本节课你学习了几种判定菱形的方法?
2、你是怎样得到这些判别方法的?
3、对本节课的学习你有什么感受和想法?
设计意图:通过问题1,让学生理清本节课的知识结构,明确菱形的三种判定方法。通过问题2和问题3,让学生对学习过程回顾和反思,感受探究过程中的乐趣,体验克服困难的过程,树立自信心。及时地总结和反思是良好的学习习惯,不同的学生所得不同,感受和体会也不相同。我们要关注这些差异,并及时总结和反思,方能教学相长。
作业布置:
1、必做题:教科书第60页习题18.2第6题,61页习题18.2第10题。
2、选做题:拓展提升,教科书58页练习第3题。
设计意图:必做题:让学生在作业中,发现问题,及时查缺补漏。选做题:巩固提高,使各层次的学生得到不同的发展。
课后反思:
有效教学是教师教与学生学的统一。学生获得知识,必须建立在自己体验和思考的基础上;学生应用知识并逐步形成技能,离不开自己的实践;学生通过自主、合作、探究的学习方式,亲身经历观察、实验、猜想、推理、论证、展示、交流等活动,才能在数学思考、问题解决、情感态度方面得到发展。尊重学生个体差异,不同的学生侧重不同的学习方式,对不同的学生学习要求不同,追求不同的学生在数学上得到不同的发展,才能实现面向全体学生的数学教学。
一、教学目标:
(1)知识目标:
经历菱形判定方法探究过程,掌握菱形三种判定方法 ,会根据菱形的三种判定方法判定一个四边形是菱形。
(2)能力目标:
1、经历利用菱形定义探究菱形其他判定方法的过程,培养学生的观察、推理的意识,发展学生的形象思维和逻辑推理能力。
2、根据菱形的判定进行简单的证明,培养学生逻辑推理能力和演绎能力。
(3)情感目标:
在探究菱形的判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心。
二、教学重点: 探索菱形判定定理的过程及应用
三、教学难点: 合理应用菱形的判定定理解决问题
四、学情分析:学生已掌握了平行四边形、矩形有关知识及菱形的定义和性质,经历过利用木条自己制作学具并进行探究的活动,对其探究方法有所了解。作为初二学生,他们的空间观念已初步建立,天生的好奇心成为孩子们学习的最好动力。经过培养我班学生具有了一定地主动探究的意识和习惯,对于自我展示有较强的渴望和一定的技能。学生学习的困难是利用所学知识对猜想和问题进行推理论证。
五、教法与学法:
1、教法
(1)创设问题情景,结合具体实例,让学生亲身经历数学知识发现和解决的过程,体验学习的快乐, 建立学习的信心。
(2)结合具体实例,让学生动脑自己归纳出结论
2、学法
观察讨论、自主探究、合作交流,猜想 验证。
六、教学资源:多媒体课件、可以转动的木条十字架、等腰三角形纸板(不等边)、三角板
七、教学过程:
(一)复习回归,导入新课
1、菱形的定义:一组邻边相等的平行四边形是菱形。
2、菱形的性质:(1)菱形的两组对边分别平行,四条边都相等;
(2) 菱形的两组对角分别相等,邻角互补;
(3)菱形的两条对角线互相平分;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
3、对称性:是轴对称图形,有两条对称轴。
4、菱形具有平行四边形的所有性质。
5、导入:
要判定一个四边形是菱形,除根据定义判定外,还有其它的判定方法吗?
(二)合作探究,自主归纳
1、学生自己制作的学具,一长一短两根木条,在它们的中点处固定一个小钉,做成一个可以转动的十字架,任意转动其中的一根木条,用笔和直尺画出木条四个端点的连线。
观察这个四边形总有什么特征?能证明你的发现吗?
设计意图:学生利用平行四边形的判定方法得出图形总是平行四边形。既为菱形的第二种判定方法的探究作好了知识上的铺垫,又巩固了平行四边形的判定方法,培养学生的观察能力和推理能力。
2、继续转动木条,观察什么时候围成的四边形变成菱形。
这时教师深入学生之中,引导学生观察,探究,深入思考。了解学生探究的过程,观察指导学生探究方法。得出结论,当两个木棒之间的夹角等于90度时,得到的图形是菱形。给学生以直观感受,印象深刻。最后,请学生代表利用学具展示说明。
学生猜想: 当两个木棒之间的夹角等于90度时,得到的图形是菱形。
(请学生代表利用学具展示说明。)
3、你能证明你的猜想吗?
(1)学生思考后小组内交流证明思路。
(2)请学生说一说思路。
(3)教师引导学生规范的文字题证明,然后学生写出证明过程并简明的点评。
已知:在□ABCD中,对角线AC⊥BD.
求证:□ABCD是菱形。
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵ AC ⊥ BD
∴ BA=BC
∴ □ABCD是菱形
(4)归纳菱形的判定定理:对角线互相垂直的平行四边形是菱形。
数学语言:
∵四边形ABCD是平行四边形,AC ⊥ BD
∴ □ ABCD是菱形
设计意图:
(1)通过制作木条,让学生初步认识图形,并利用平行四边形的判定方法得出图形总是平行四边形。既为菱形的第二种判定方法的探究作好了知识上的铺垫,又巩固了平行四边形的判定方法,培养学生的合情推理能力。
(2)通过实验操作,让学生带着问题,经历探究物体与图形的形状、大小位置关系和变换的过程,感受动手实验的乐趣,培养猜想的意识,感受直观操作得出猜想的便捷性,培养学生观察、实验、猜想等合情推理能力。
(3)通过猜想和论证,进一步突出图形性质的探索过程,直观操作和逻辑推理有机结合,进一步让学生认识到逻辑推理的必要性,进一步让学生感受到逻辑推理是得出结论的重要手段,很好的突出了教学的重点。
(三)尝试练习,学以致用
例 如图,如图,□ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3,求证:□ABCD是菱形。
1、学生充分思考后,交流不同的思路。教师引导学生选择恰当的方法。
2、教师指导学生完成规范证明。教师出示规范的板演,学生进行对照学习。
设计意图:根据已知条件明确思路、选择恰当的方法是问题解决的基本策略,学生经过独立思考、讨论交流、规范证明等过程,进一步培养推理论证、解决问题的能力。
(四)再次合作,探究新知
让学生拿出课前准备的两个全等的等腰三角形纸板(不等边),小组交流,开动脑筋,动手拼一拼,看一下可以拼出几种平行四边形。
1、问题解决:当两底边重合时拼出的四边形是什么图形?它的四条边有什么样的数量关系
2、思考与归纳:你能得到什么结论?
3、学生代表展示作品,并利用作品说明结论。 最后得出:四边相等的四边形是菱形。教师指导学生规范完成几何论证过程。
4、归纳菱形的判定定理:四边相等的四边形是菱形。
设计意图:这一探究活动贴近生活、轻松自然。学生利用平行四边形的判定和菱形的定义,演示说明自己的作品就是菱形,进一步培养了推理论证能力,体验了数学与生活的密切联系,产生了极大的成就感。
学生展示几何论证过程:
已知:在四边形ABCD中,AB=BC=CD=DA。
求证:四边形ABCD是菱形
证明:∵AD=BC AB=CD
∴四边形ABCD是平行四边形
又∵AB=AD
∴四边形ABCD是菱形
归纳菱形的判定定理:四条边都相等的四边形是菱形。
数学语言:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
(五)练习巩固
学生独立思考,教师点拨证明的思路。学生板演,教师点评。
设计意图:通过添加复习题上的一题,学生在做题之后,进一步掌握四边相等的四边形是菱形的这一判定方法。既巩固了三角形的中位线定理和矩形的性质,又达到了学以致用的目的,培养了学生的应用意识。
(六)随堂练习
一个平行四边形的一条边长是9,两条对角线的长分别是12和
6,这是一个特殊的平行四边形吗?为什么?求出它的面积。
设计意图:进一步培养根据已知条件和对图形的观察进行合情推理,选择合适的判定方法进行推理论证的能力。
(七)总结和反思
1、本节课你学习了几种判定菱形的方法?
2、你是怎样得到这些判别方法的?
3、对本节课的学习你有什么感受和想法?
设计意图:通过问题1,让学生理清本节课的知识结构,明确菱形的三种判定方法。通过问题2和问题3,让学生对学习过程回顾和反思,感受探究过程中的乐趣,体验克服困难的过程,树立自信心。及时地总结和反思是良好的学习习惯,不同的学生所得不同,感受和体会也不相同。我们要关注这些差异,并及时总结和反思,方能教学相长。
作业布置:
1、必做题:教科书第60页习题18.2第6题,61页习题18.2第10题。
2、选做题:拓展提升,教科书58页练习第3题。
设计意图:必做题:让学生在作业中,发现问题,及时查缺补漏。选做题:巩固提高,使各层次的学生得到不同的发展。
课后反思:
有效教学是教师教与学生学的统一。学生获得知识,必须建立在自己体验和思考的基础上;学生应用知识并逐步形成技能,离不开自己的实践;学生通过自主、合作、探究的学习方式,亲身经历观察、实验、猜想、推理、论证、展示、交流等活动,才能在数学思考、问题解决、情感态度方面得到发展。尊重学生个体差异,不同的学生侧重不同的学习方式,对不同的学生学习要求不同,追求不同的学生在数学上得到不同的发展,才能实现面向全体学生的数学教学。
