北京市平谷区2019-2020学年高二下学期期末质量监控数学试题 Word版含答案
文档属性
| 名称 | 北京市平谷区2019-2020学年高二下学期期末质量监控数学试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-03 00:00:00 | ||
图片预览




文档简介
平谷区2019—2020学年度第二学期质量监控试卷
高二数学
2020.6
第Ⅰ卷选择题(共40分)
—、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的.)
在复平面内,复数对应的点的坐标是
2.知抛物线,那么其焦点到准线的距离是
A.2
B.4
C.6
D.8
3.已知等差数列}中那么
A.17
B.9
C.
10
D.
24
4,已知直线与圆相切,那么a的值为
A.3或-1
B.
C.-3或-7
D.
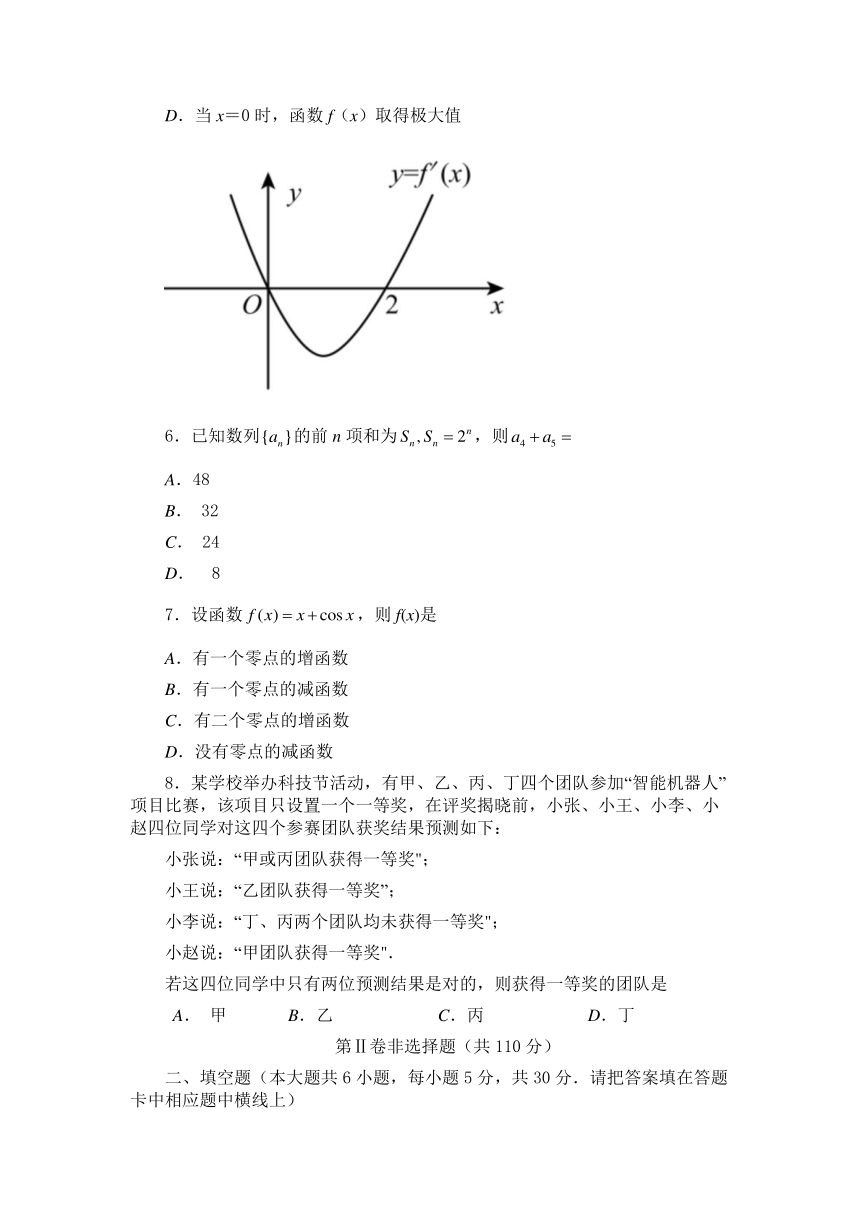
5.已知函数f(x)的导函数图像如图所示,那么下列说法正确的是
A.函数f(x)在上单调递减
B.函数f(x)有三个零点
C.当x=0时,函数f(x)取得最大值
D.当x=0时,函数f(x)取得极大值
6.已知数列的前n项和为,则
A.48
B.
32
C.
24
D.
8
7.设函数,则f(x)是
A.有一个零点的增函数
B.有一个零点的减函数
C.有二个零点的增函数
D.没有零点的减函数
8.某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖,在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:
小张说:“甲或丙团队获得一等奖";
小王说:“乙团队获得一等奖”;
小李说:“丁、丙两个团队均未获得一等奖";
小赵说:“甲团队获得一等奖".
若这四位同学中只有两位预测结果是对的,则获得一等奖的团队是
A.
甲
B.乙
C.丙
D.丁
第Ⅱ卷非选择题(共110分)
二、填空题(本大题共6小题,每小题5分,共30分.请把答案填在答题卡中相应题中横线上)
9.已知复数,那么________
10.已知直线与直线互相垂直,那么b=________
11.已知双曲线的一个焦点为(3,0),一个顶点为(1,0),那么其渐近线方程为________
12.已知等差数列中,,等比数列中,
,那么数列的前4项和________
13.已知双曲线的一个焦点与抛物线的焦点重合,且焦点到渐近线的距离为,那么双曲线的离心率为________
14.日常生活中的饮用水通常都是经过净化的,随着水纯净度的提高,所需净化费用不断增加.已知1t水净化到纯净度为x%时所需费用(单位:元)为.那么净化到纯净度为90%时所需净化费用的瞬时变化率是________元/t.
三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
)
15.
(本题满分13分)
已知函数
(Ⅰ)求曲线在点(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)在[—2,2]上的最大值和最小值.
16.
(本题满分13分)
设是等差数列的前n项和,,________.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前n项和的最值.
从中任选一个,补充在上面的问题中并作答.
(注:如果选择多个条件分别解答,按第一个解答计分).
17.
(本题满分13分)
已知椭圆的离心率为,过点(2,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设左、右焦点分别为,经过右焦点F2的直线l与椭圆C相交于A、B两点,若,求直线l方程。
18.
(本题满分14分)已知函数
(Ⅰ)若函数f(x)在x=e处取得极值,求a的值;
(Ⅱ)若对所有,都有f(x),求实数a的取值范围.
19.(本题满分14分)
已知椭圆C:的左、右焦点分别为,椭圆上一点满足.
(I)求椭圆C的方程;
(Ⅱ)已知椭圆C上两点M、N关于x轴对称,点P为椭圆上一动点(不与M、N重合),若直线PM,PN与
轴分别交于G、H两点,证明:为定值.
20.(本题满分13分)
定义首项为1,且公比为正数的等比数列为"M—数列”
(Ⅰ)已知数列是单调递增的等差数列,满足,求数列的通项公式;
(Ⅱ)已知数列的前n项和为,若是和1的等差中项,证明:数列是"M-数列";
(Ⅲ)在(Ⅰ)的条件下,若存在"M—数列”
,对于任意正整数k,都有成立.求此时数列公比q的最小值.
平谷区2019-2020学年度第二学期教学试卷参考答案
高二数学
2020.6
一.选择题:本大题共8小题,每小题5分,共40分.
题号
1
2
3
4
5
6
7
8
答案
C
B
B
A
D
C
A
B
二.填空题:本大题共6小题,每小题5分,共30分.
9.
;
10.
2;
11.
;
12.
320;
13.
14.
40.15
三、解答题:本大题共6小题,共80分;解答应写出文字说明,证明过程或演算步骤).
15.(本小题满分13分)
解:(I)因为,
………
2分
,即切线的斜率
………4分
又因为,即切点坐标为,
………
6分
所以曲线在点处的切线方程为.………
7分
(II)由,令,
………
8分
-2
-1
0
2
+
0
0
+
0
2
16
所以的最大值为16,最小值为0.
………13分
16.(本小题满分13分)
选①补充条件.
解:(I)设等差数列的公差为,
由,,得,解得,
所以.
………
7分
(II)解法1:由等差数列的通项公式可知,数列是单调递增数列,且首项为1,所以前项和有最小值,无最大值,且最小值为.
解法2:由数列的前项和
由二次函数图像性质可知,当时有最小值1,无最大值.
………
13分
选②补充条件.
解:(I)设等差数列的公差为,因为
,所以
由,
所以.
………7分
(II)解法1:因为,所以等差数列是单调递减数列.
令,,,所以前5项和为的最大值.
即前项和的最大值为,无最小值.
解法2:因为数列的前项和
由二次函数图像性质可知,当时有最大值,无最小值.
………
13分
选③补充条件.
解:(I)设等差数列的公差为,
由,,得,
解得,
所以.
………
7分
(II)解法1:因为,所以等差数列是单调递减数列.
令,,,即当时前项和有最大值.
所以前项和的最大值为,无最小值.
解法2:数列的前项和
由二次函数图像性质可知,当时有最大值45,无最小值.
……
13分
17.
(本小题满分13分)
解:(Ⅰ),且过点.
∴,
………
2分
∴
∴椭圆的标准方程为:;
………
4分
(Ⅱ)当斜率不存在时,设:,
得
显然不满足条件.
………6分
当斜率存在时设:,、,………
7分
联立整理得:,
∴,
………
9分
因为,
所以
即:
整理得
………
11分
带入化简:
∴直线方程为.
………
13分
18.(本小题满分14分)
解:(I)由得………
2分
因为函数在处取得极值,
所以,
………4分
解得
………5分
经检验,时,函数在处取得极大值.
所以
………
6分
(II)
因为对所有,都有,
所以
………
8分
设
则
………10分
因为,所以,
即在上单调递减
………12分
所以
即
………14分
19.(本小题满分14分)
解:(I)由椭圆上一点
满足.
得
………
2分
且
………
3分
所以
所以椭圆的方程为.
………
4分
(II)证明:因为,两点关于轴对称,
所以设,,则,
………
5分
得直线的方程为,
令得点的横坐标,
同理可得点的横坐标
.
………9分
∴,………
11分
因为,
∴,.
………
13分
即得:为定值.
………
14分
20.(本小题满分13分)
解:(I)因为是等差数列,
所以
………
1分
又因为是递增等差数列,
所以
即数列的通项公式为
………
3分
(II)因为是和1的等差中项,
所以
………
4分
当时,
………
5分
当时,
化简得
即数列是首项为1,公比为2的等比数列.
所以数列是“M-数列”.
………
7分
(III)因为数列是
“M-数列”
所以数列是首项为1,公比为正数的等比数列,设公比为,
则.
………
8分
因为对于任意正整数,都有成立,
即恒成立
两边取对数得
………
9分
设
则
令
即
即
所以比较大小
而
所以
………
11分
即
因为
所以
所以数列公比的最小值为.
………13分
高二数学
2020.6
第Ⅰ卷选择题(共40分)
—、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的.)
在复平面内,复数对应的点的坐标是
2.知抛物线,那么其焦点到准线的距离是
A.2
B.4
C.6
D.8
3.已知等差数列}中那么
A.17
B.9
C.
10
D.
24
4,已知直线与圆相切,那么a的值为
A.3或-1
B.
C.-3或-7
D.
5.已知函数f(x)的导函数图像如图所示,那么下列说法正确的是
A.函数f(x)在上单调递减
B.函数f(x)有三个零点
C.当x=0时,函数f(x)取得最大值
D.当x=0时,函数f(x)取得极大值
6.已知数列的前n项和为,则
A.48
B.
32
C.
24
D.
8
7.设函数,则f(x)是
A.有一个零点的增函数
B.有一个零点的减函数
C.有二个零点的增函数
D.没有零点的减函数
8.某学校举办科技节活动,有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛,该项目只设置一个一等奖,在评奖揭晓前,小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下:
小张说:“甲或丙团队获得一等奖";
小王说:“乙团队获得一等奖”;
小李说:“丁、丙两个团队均未获得一等奖";
小赵说:“甲团队获得一等奖".
若这四位同学中只有两位预测结果是对的,则获得一等奖的团队是
A.
甲
B.乙
C.丙
D.丁
第Ⅱ卷非选择题(共110分)
二、填空题(本大题共6小题,每小题5分,共30分.请把答案填在答题卡中相应题中横线上)
9.已知复数,那么________
10.已知直线与直线互相垂直,那么b=________
11.已知双曲线的一个焦点为(3,0),一个顶点为(1,0),那么其渐近线方程为________
12.已知等差数列中,,等比数列中,
,那么数列的前4项和________
13.已知双曲线的一个焦点与抛物线的焦点重合,且焦点到渐近线的距离为,那么双曲线的离心率为________
14.日常生活中的饮用水通常都是经过净化的,随着水纯净度的提高,所需净化费用不断增加.已知1t水净化到纯净度为x%时所需费用(单位:元)为.那么净化到纯净度为90%时所需净化费用的瞬时变化率是________元/t.
三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
)
15.
(本题满分13分)
已知函数
(Ⅰ)求曲线在点(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)在[—2,2]上的最大值和最小值.
16.
(本题满分13分)
设是等差数列的前n项和,,________.
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前n项和的最值.
从中任选一个,补充在上面的问题中并作答.
(注:如果选择多个条件分别解答,按第一个解答计分).
17.
(本题满分13分)
已知椭圆的离心率为,过点(2,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设左、右焦点分别为,经过右焦点F2的直线l与椭圆C相交于A、B两点,若,求直线l方程。
18.
(本题满分14分)已知函数
(Ⅰ)若函数f(x)在x=e处取得极值,求a的值;
(Ⅱ)若对所有,都有f(x),求实数a的取值范围.
19.(本题满分14分)
已知椭圆C:的左、右焦点分别为,椭圆上一点满足.
(I)求椭圆C的方程;
(Ⅱ)已知椭圆C上两点M、N关于x轴对称,点P为椭圆上一动点(不与M、N重合),若直线PM,PN与
轴分别交于G、H两点,证明:为定值.
20.(本题满分13分)
定义首项为1,且公比为正数的等比数列为"M—数列”
(Ⅰ)已知数列是单调递增的等差数列,满足,求数列的通项公式;
(Ⅱ)已知数列的前n项和为,若是和1的等差中项,证明:数列是"M-数列";
(Ⅲ)在(Ⅰ)的条件下,若存在"M—数列”
,对于任意正整数k,都有成立.求此时数列公比q的最小值.
平谷区2019-2020学年度第二学期教学试卷参考答案
高二数学
2020.6
一.选择题:本大题共8小题,每小题5分,共40分.
题号
1
2
3
4
5
6
7
8
答案
C
B
B
A
D
C
A
B
二.填空题:本大题共6小题,每小题5分,共30分.
9.
;
10.
2;
11.
;
12.
320;
13.
14.
40.15
三、解答题:本大题共6小题,共80分;解答应写出文字说明,证明过程或演算步骤).
15.(本小题满分13分)
解:(I)因为,
………
2分
,即切线的斜率
………4分
又因为,即切点坐标为,
………
6分
所以曲线在点处的切线方程为.………
7分
(II)由,令,
………
8分
-2
-1
0
2
+
0
0
+
0
2
16
所以的最大值为16,最小值为0.
………13分
16.(本小题满分13分)
选①补充条件.
解:(I)设等差数列的公差为,
由,,得,解得,
所以.
………
7分
(II)解法1:由等差数列的通项公式可知,数列是单调递增数列,且首项为1,所以前项和有最小值,无最大值,且最小值为.
解法2:由数列的前项和
由二次函数图像性质可知,当时有最小值1,无最大值.
………
13分
选②补充条件.
解:(I)设等差数列的公差为,因为
,所以
由,
所以.
………7分
(II)解法1:因为,所以等差数列是单调递减数列.
令,,,所以前5项和为的最大值.
即前项和的最大值为,无最小值.
解法2:因为数列的前项和
由二次函数图像性质可知,当时有最大值,无最小值.
………
13分
选③补充条件.
解:(I)设等差数列的公差为,
由,,得,
解得,
所以.
………
7分
(II)解法1:因为,所以等差数列是单调递减数列.
令,,,即当时前项和有最大值.
所以前项和的最大值为,无最小值.
解法2:数列的前项和
由二次函数图像性质可知,当时有最大值45,无最小值.
……
13分
17.
(本小题满分13分)
解:(Ⅰ),且过点.
∴,
………
2分
∴
∴椭圆的标准方程为:;
………
4分
(Ⅱ)当斜率不存在时,设:,
得
显然不满足条件.
………6分
当斜率存在时设:,、,………
7分
联立整理得:,
∴,
………
9分
因为,
所以
即:
整理得
………
11分
带入化简:
∴直线方程为.
………
13分
18.(本小题满分14分)
解:(I)由得………
2分
因为函数在处取得极值,
所以,
………4分
解得
………5分
经检验,时,函数在处取得极大值.
所以
………
6分
(II)
因为对所有,都有,
所以
………
8分
设
则
………10分
因为,所以,
即在上单调递减
………12分
所以
即
………14分
19.(本小题满分14分)
解:(I)由椭圆上一点
满足.
得
………
2分
且
………
3分
所以
所以椭圆的方程为.
………
4分
(II)证明:因为,两点关于轴对称,
所以设,,则,
………
5分
得直线的方程为,
令得点的横坐标,
同理可得点的横坐标
.
………9分
∴,………
11分
因为,
∴,.
………
13分
即得:为定值.
………
14分
20.(本小题满分13分)
解:(I)因为是等差数列,
所以
………
1分
又因为是递增等差数列,
所以
即数列的通项公式为
………
3分
(II)因为是和1的等差中项,
所以
………
4分
当时,
………
5分
当时,
化简得
即数列是首项为1,公比为2的等比数列.
所以数列是“M-数列”.
………
7分
(III)因为数列是
“M-数列”
所以数列是首项为1,公比为正数的等比数列,设公比为,
则.
………
8分
因为对于任意正整数,都有成立,
即恒成立
两边取对数得
………
9分
设
则
令
即
即
所以比较大小
而
所以
………
11分
即
因为
所以
所以数列公比的最小值为.
………13分
同课章节目录
