苏科版九下数学 6.6图形的位似教案(习题无答案)
文档属性
| 名称 | 苏科版九下数学 6.6图形的位似教案(习题无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 00:00:00 | ||
图片预览

文档简介
图形的位似
教学目标:
1.了解位似多边形及其有关概念,了解位似与相似的联系和区别,掌握位似多边形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
教学重点:
位似多边形的有关概念、性质与作图.
教学难点:
利用位似将一个图形放大或缩小.
课前参与:
把幻灯片上的图形放大到屏幕上,形成的新图形和原图形就是典型的位似图形。
1.位似形的相关概念
如果两个图形相似,而且对应点的连线相交于一点,那么这两个图形叫做位似形,这个交点叫做位似中心.
说明:位似形一定是相似形,但相似形不一定是位似形.
2.位似形的意义及画法
(1)意义:利用位似形可以将一个图形________或________.
(2)画法:以△ABC为例,将△ABC扩大n倍(或缩小),得到△A'B'C'.
①确定位似中心O,连接OA、OB、OC;
②延长(或反向延长)OA、OB、OC;
③在延长线(或反向延长线)OA上取OA'=n·OA,在延长线(或反向延长线)OB上取OB'=n·OB,在延长线(或反向延长线)OC上取OC'=n·OC;
④顺次连接A'B'、B'C'、C'A',则△A'B'C'就是所画的图形.
3.位似形的性质
如图,若△A'B'C'与△ABC位似,相似比为k.
(1)
∵,∠A'OC'=∠AOC,
∴△________∽△________.
∴________,同理,________.
归纳:在位似形中,各对应点到位似中心的距离之比等于________。有时称位似图形的位似比就是相似比(注意:对应点重合除外).
(2)∵,∠A'OC'=∠AOC,
∴△________∽△________.
∴∠________=∠________.∴A'C'____AC.同理,B'C'____BC,A'B'_____AB.
归纳:在位似形中,各对应边____________(注意:对应边所在的直线重合除外).
课中参与:
例1
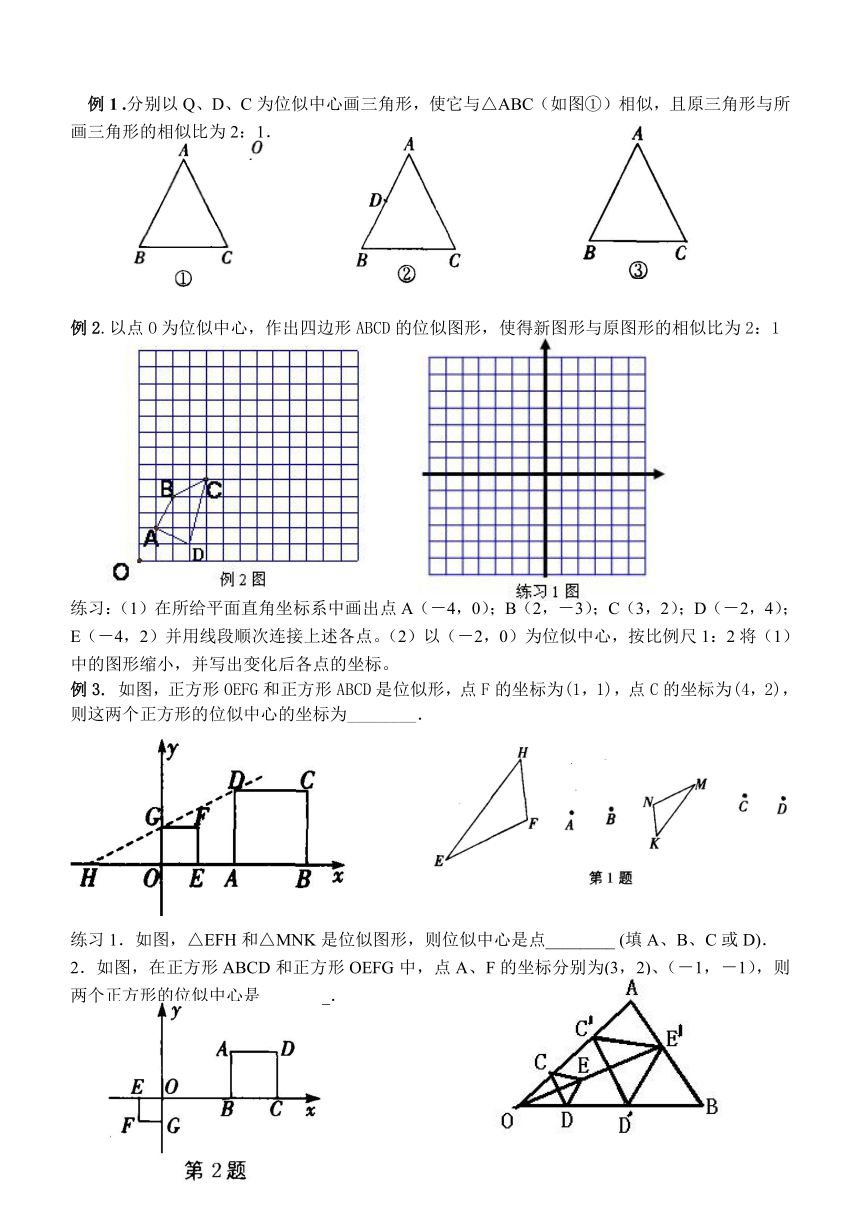
.分别以Q、D、C为位似中心画三角形,使它与△ABC(如图①)相似,且原三角形与所画三角形的相似比为2:1.
例2.以点O为位似中心,作出四边形ABCD的位似图形,使得新图形与原图形的相似比为2:1
练习:(1)在所给平面直角坐标系中画出点A(-4,0);B(2,-3);C(3,2);D(-2,4);E(-4,2)并用线段顺次连接上述各点。(2)以(-2,0)为位似中心,按比例尺1:2将(1)中的图形缩小,并写出变化后各点的坐标。
例3.
如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形的位似中心的坐标为________.
练习1.如图,△EFH和△MNK是位似图形,则位似中心是点________
(填A、B、C或D).
2.如图,在正方形ABCD和正方形OEFG中,点A、F的坐标分别为(3,2)、(-1,-1),则两个正方形的位似中心是________.
例4题图
例4.如图,用下面的方法可以画△AOB的“内接等边三角形”。阅读后证明相应的问题。
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②
连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,
作E′D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接三角形。
请你判断△C′D′E′是否是等边三角形,并说明理由。
课后参与
1.用作位似形的方法,可以将一个图形放大或缩小,位似中心(
)
A.只能选在原图形的外部
B.只能选在原图形的内部
C.只能选在原图形的边上
D.可以选择任意位置
2.下列说法正确的个数是( )
①位似图形一定是相似图形
②相似图形一定是位似图形
③两个位似图形若全等,则位似中心一定在两个图形之间
④若四边形ABCD与四边形EFGH是位似图形,则其中△ABC与△FEG也是位似图形
A.1个
B.2个 C.3个
D.4个
3.设四边形ABCD与四边形A′B′C′D′是位似图形,且位似比为k。给出下列4个等式:①;②△ABC∽△A′B′C′③④。其中,等式成立的个数为(
)
(A)1个
(B)2个
(C)3个
(D)4个
4.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a
,b),那么大“鱼”上对应“顶点”的坐标为(
)
A.(-a,-2b)
B.(-2a,-b)
C.(-2a,-2b)
D.(-2b,-2a)
第4题
第5题
第6题
5.如下图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则为(
)
A.
B.
C.
D.
6.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为(
)
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
7.五边形ABCDE位似于五边形A′B′C′D′E′,它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A′的距离为___________
8.如图,以菱形ABCD的对角线所在的直线为坐标
轴建立直角坐标系,以点O为位似中心,在图中画一个
与已知菱形位似的菱形,使其面积扩大4倍.
9.如图,在矩形ABCD中,以对角线AC、BD的交点O为位似中心,解答以下问题:
(1)按新图与已知图形的相似比为和2作两个矩形A1B1C1D1和A2B2C2D2
(2)求△OA1B1和四边形A1D1D2A2的面积之比.
10.如图,直角梯形ABCD中,AB∥DC,∠ABC=90°,AD=BD,AC与BD相交于点E,
AC⊥BD,过点E作EF∥AB,交AD于点F。
①说明AF=BE的理由;
②AF2与AE·EC有什么样的数量关系?为什么?
11.如图,点E、F分别是平行四边形ABCD的边AB和CD的延长线上的点,连接EF,分别交AD、BC于点H、G,写出图中的位似三角形.
12.在给定的锐角△ABC中,求作一个正方形DEFG,使D、E落在BC上,F、G分别落在AC、AB边上,作法如下:
第一步:画出一个有3个顶点落在△ABC两边上的正方形D1E1F1G1;
第二步:连结BF1,并延长交AC于点F;
第三步:过F点作FE⊥BC交AB于点E;第四步:过F点作FG∥BC交AB于点G;第五步:过G点作GD⊥BC于点D.四边形DEFG即为所求作的正方形DEFG.
根据以上作图步骤,回答以下问题:
(1)上述所求作的四边形DEFG是正方形吗?为什么?
(2)在△ABC中,如果BC=10,高AQ=6,求上述正方形DEFG的边长.
A
B
C
D
E
F
G
G1
D1
E1
F1
PAGE
教学目标:
1.了解位似多边形及其有关概念,了解位似与相似的联系和区别,掌握位似多边形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
教学重点:
位似多边形的有关概念、性质与作图.
教学难点:
利用位似将一个图形放大或缩小.
课前参与:
把幻灯片上的图形放大到屏幕上,形成的新图形和原图形就是典型的位似图形。
1.位似形的相关概念
如果两个图形相似,而且对应点的连线相交于一点,那么这两个图形叫做位似形,这个交点叫做位似中心.
说明:位似形一定是相似形,但相似形不一定是位似形.
2.位似形的意义及画法
(1)意义:利用位似形可以将一个图形________或________.
(2)画法:以△ABC为例,将△ABC扩大n倍(或缩小),得到△A'B'C'.
①确定位似中心O,连接OA、OB、OC;
②延长(或反向延长)OA、OB、OC;
③在延长线(或反向延长线)OA上取OA'=n·OA,在延长线(或反向延长线)OB上取OB'=n·OB,在延长线(或反向延长线)OC上取OC'=n·OC;
④顺次连接A'B'、B'C'、C'A',则△A'B'C'就是所画的图形.
3.位似形的性质
如图,若△A'B'C'与△ABC位似,相似比为k.
(1)
∵,∠A'OC'=∠AOC,
∴△________∽△________.
∴________,同理,________.
归纳:在位似形中,各对应点到位似中心的距离之比等于________。有时称位似图形的位似比就是相似比(注意:对应点重合除外).
(2)∵,∠A'OC'=∠AOC,
∴△________∽△________.
∴∠________=∠________.∴A'C'____AC.同理,B'C'____BC,A'B'_____AB.
归纳:在位似形中,各对应边____________(注意:对应边所在的直线重合除外).
课中参与:
例1
.分别以Q、D、C为位似中心画三角形,使它与△ABC(如图①)相似,且原三角形与所画三角形的相似比为2:1.
例2.以点O为位似中心,作出四边形ABCD的位似图形,使得新图形与原图形的相似比为2:1
练习:(1)在所给平面直角坐标系中画出点A(-4,0);B(2,-3);C(3,2);D(-2,4);E(-4,2)并用线段顺次连接上述各点。(2)以(-2,0)为位似中心,按比例尺1:2将(1)中的图形缩小,并写出变化后各点的坐标。
例3.
如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形的位似中心的坐标为________.
练习1.如图,△EFH和△MNK是位似图形,则位似中心是点________
(填A、B、C或D).
2.如图,在正方形ABCD和正方形OEFG中,点A、F的坐标分别为(3,2)、(-1,-1),则两个正方形的位似中心是________.
例4题图
例4.如图,用下面的方法可以画△AOB的“内接等边三角形”。阅读后证明相应的问题。
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②
连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,
作E′D′∥ED,交OB于点D′;
③连接C′D′,则△C′D′E′是△AOB的内接三角形。
请你判断△C′D′E′是否是等边三角形,并说明理由。
课后参与
1.用作位似形的方法,可以将一个图形放大或缩小,位似中心(
)
A.只能选在原图形的外部
B.只能选在原图形的内部
C.只能选在原图形的边上
D.可以选择任意位置
2.下列说法正确的个数是( )
①位似图形一定是相似图形
②相似图形一定是位似图形
③两个位似图形若全等,则位似中心一定在两个图形之间
④若四边形ABCD与四边形EFGH是位似图形,则其中△ABC与△FEG也是位似图形
A.1个
B.2个 C.3个
D.4个
3.设四边形ABCD与四边形A′B′C′D′是位似图形,且位似比为k。给出下列4个等式:①;②△ABC∽△A′B′C′③④。其中,等式成立的个数为(
)
(A)1个
(B)2个
(C)3个
(D)4个
4.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a
,b),那么大“鱼”上对应“顶点”的坐标为(
)
A.(-a,-2b)
B.(-2a,-b)
C.(-2a,-2b)
D.(-2b,-2a)
第4题
第5题
第6题
5.如下图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则为(
)
A.
B.
C.
D.
6.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为(
)
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
7.五边形ABCDE位似于五边形A′B′C′D′E′,它们的面积比为4:9,已知位似中心O到A点的距离为6,那么O到A′的距离为___________
8.如图,以菱形ABCD的对角线所在的直线为坐标
轴建立直角坐标系,以点O为位似中心,在图中画一个
与已知菱形位似的菱形,使其面积扩大4倍.
9.如图,在矩形ABCD中,以对角线AC、BD的交点O为位似中心,解答以下问题:
(1)按新图与已知图形的相似比为和2作两个矩形A1B1C1D1和A2B2C2D2
(2)求△OA1B1和四边形A1D1D2A2的面积之比.
10.如图,直角梯形ABCD中,AB∥DC,∠ABC=90°,AD=BD,AC与BD相交于点E,
AC⊥BD,过点E作EF∥AB,交AD于点F。
①说明AF=BE的理由;
②AF2与AE·EC有什么样的数量关系?为什么?
11.如图,点E、F分别是平行四边形ABCD的边AB和CD的延长线上的点,连接EF,分别交AD、BC于点H、G,写出图中的位似三角形.
12.在给定的锐角△ABC中,求作一个正方形DEFG,使D、E落在BC上,F、G分别落在AC、AB边上,作法如下:
第一步:画出一个有3个顶点落在△ABC两边上的正方形D1E1F1G1;
第二步:连结BF1,并延长交AC于点F;
第三步:过F点作FE⊥BC交AB于点E;第四步:过F点作FG∥BC交AB于点G;第五步:过G点作GD⊥BC于点D.四边形DEFG即为所求作的正方形DEFG.
根据以上作图步骤,回答以下问题:
(1)上述所求作的四边形DEFG是正方形吗?为什么?
(2)在△ABC中,如果BC=10,高AQ=6,求上述正方形DEFG的边长.
A
B
C
D
E
F
G
G1
D1
E1
F1
PAGE
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
