苏科版九下数学第6章相似三角形复习教案
文档属性
| 名称 | 苏科版九下数学第6章相似三角形复习教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 120.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 00:00:00 | ||
图片预览

文档简介
相似三角形复习教案
教学目标
:
1.
进一步掌握相似三角形的判定方法和性质。
2.
会用相似三角形的判定方法和性质解决问题。
能力目标:
1.
进一步培养学生对相似三角形的性质与判定知识的理解能力。
2.
培养学生的思维能力和合作能力。
教学重点:
相似三角形的性质与判定的应用
教学难点:
相似三角形的综合应用能力
教学过程:
1.
知识回顾:
1.什么叫相似三角形?
2.相似三角形的判定方法有哪些?
3.
相似三角形的性质有哪些?
二.典型题型
1.如图所示,D、E分别是△ABC边AB、AC上的点,请你添加一个条件,
使△ABC
与△AED相似,你添加的条件是__________.
2.如图在△ABC中,D.E分别在AB.AC上,DE//BC,AD:AB=1:3,DE=2,
则BC=______
(第1题)
(第2题)
3
.雨后初晴,一学生在运动场上玩耍,从他前面2m远一块小积水处,
他看到了旗杆的倒影,如果旗杆底端到积水处的距离为40
m,
该生眼睛的高度是1.5
m,那么旗杆的高度是______
4.如图∠1=∠2,DE:BC=2:3,AE=4,则AC=_____
5、如图,已知∠EBC=∠ABD,∠ACB=∠DEB;AB:BD=3:2,
△ABC的周长
为9,则△BDE的周长为=____
(第3题)
(第4题)
(第5题)
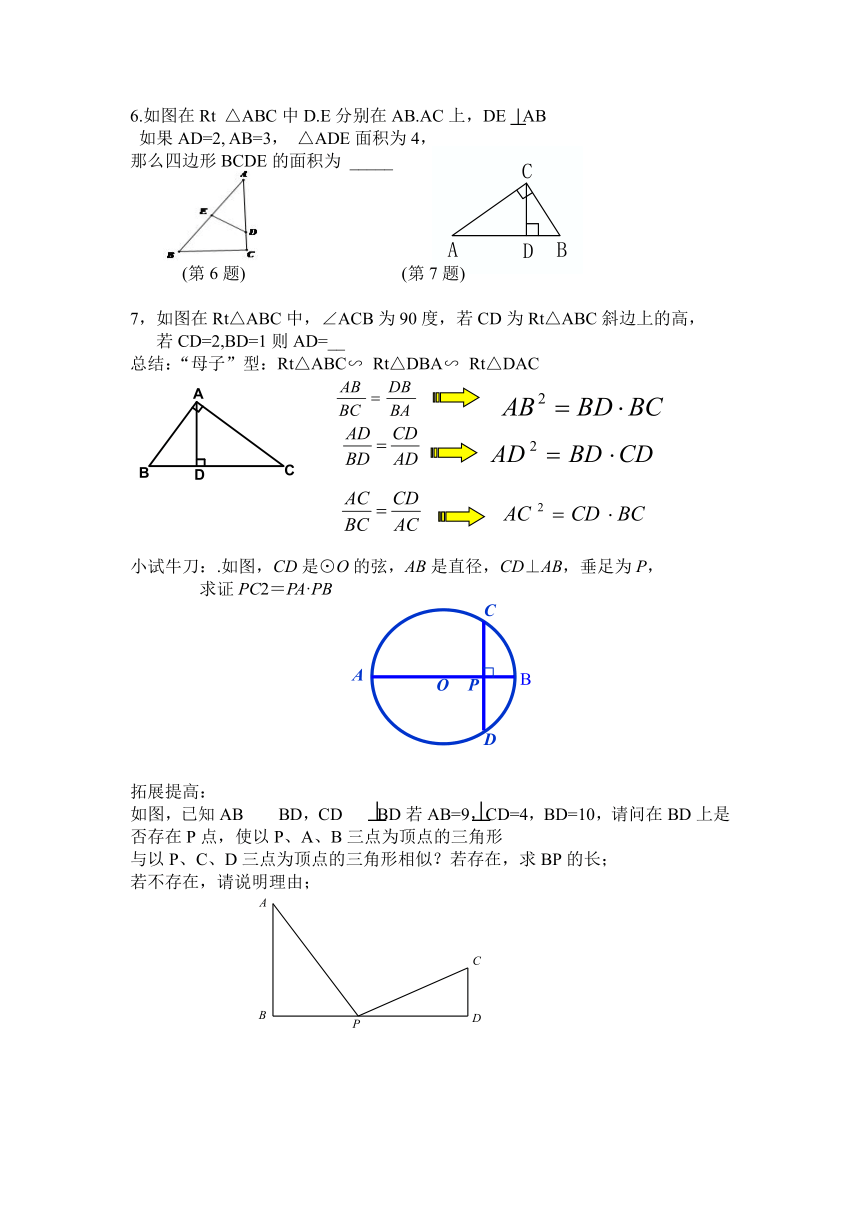
6.如图在Rt
△ABC中D.E分别在AB.AC上,DE
AB
如果AD=2,
AB=3,
△ADE面积为4,
那么四边形BCDE的面积为
_____
(第6题)
(第7题)
7,如图在Rt△ABC中,∠ACB为90度,若CD为Rt△ABC斜边上的高,
若CD=2,BD=1则AD=__
总结:“母子”型:Rt△ABC∽
Rt△DBA∽
Rt△DAC
小试牛刀:.如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,
求证PC2=PA·PB
B
拓展提高:
如图,已知AB
BD,CD
BD若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形
与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;
若不存在,请说明理由;
归纳总结:相似三角形的几种基本图形
(1)如图:称为“平行线型”的相似三角形(有“A型”与“X型”图)
(2)
如图:其中∠1=∠2,则△ADE∽△ABC称为“斜交型”的相似三角形。
(3)如图:已知∠1=∠2,∠B=∠D,则△ADE∽△ABC,
称为“旋转型”的相似三角形。
(4)如图:称“垂直型”(有“母子型”、“K型”)
三.综合运用
1.如图,抛物线经过A,C,D三点,且三点坐标为
A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(1)B点的坐标为
;
(2)是否存在F点,使四边形DFBG为矩形,
如存在求出F点坐标,如不存在,说明理由
2.
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),
D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,
且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,
设运动时间为t秒.
(1)填空:点A坐标为______;抛物线的解析式为______
.
(2)在图中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,
同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在(2)的条件下,当t为何值时,D.Q.P三点共线?
四小结
通过这节课的复习,你又增加了哪些收获?能与大家一起分享吗?
A
C
D
O
P
教学目标
:
1.
进一步掌握相似三角形的判定方法和性质。
2.
会用相似三角形的判定方法和性质解决问题。
能力目标:
1.
进一步培养学生对相似三角形的性质与判定知识的理解能力。
2.
培养学生的思维能力和合作能力。
教学重点:
相似三角形的性质与判定的应用
教学难点:
相似三角形的综合应用能力
教学过程:
1.
知识回顾:
1.什么叫相似三角形?
2.相似三角形的判定方法有哪些?
3.
相似三角形的性质有哪些?
二.典型题型
1.如图所示,D、E分别是△ABC边AB、AC上的点,请你添加一个条件,
使△ABC
与△AED相似,你添加的条件是__________.
2.如图在△ABC中,D.E分别在AB.AC上,DE//BC,AD:AB=1:3,DE=2,
则BC=______
(第1题)
(第2题)
3
.雨后初晴,一学生在运动场上玩耍,从他前面2m远一块小积水处,
他看到了旗杆的倒影,如果旗杆底端到积水处的距离为40
m,
该生眼睛的高度是1.5
m,那么旗杆的高度是______
4.如图∠1=∠2,DE:BC=2:3,AE=4,则AC=_____
5、如图,已知∠EBC=∠ABD,∠ACB=∠DEB;AB:BD=3:2,
△ABC的周长
为9,则△BDE的周长为=____
(第3题)
(第4题)
(第5题)
6.如图在Rt
△ABC中D.E分别在AB.AC上,DE
AB
如果AD=2,
AB=3,
△ADE面积为4,
那么四边形BCDE的面积为
_____
(第6题)
(第7题)
7,如图在Rt△ABC中,∠ACB为90度,若CD为Rt△ABC斜边上的高,
若CD=2,BD=1则AD=__
总结:“母子”型:Rt△ABC∽
Rt△DBA∽
Rt△DAC
小试牛刀:.如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,
求证PC2=PA·PB
B
拓展提高:
如图,已知AB
BD,CD
BD若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形
与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;
若不存在,请说明理由;
归纳总结:相似三角形的几种基本图形
(1)如图:称为“平行线型”的相似三角形(有“A型”与“X型”图)
(2)
如图:其中∠1=∠2,则△ADE∽△ABC称为“斜交型”的相似三角形。
(3)如图:已知∠1=∠2,∠B=∠D,则△ADE∽△ABC,
称为“旋转型”的相似三角形。
(4)如图:称“垂直型”(有“母子型”、“K型”)
三.综合运用
1.如图,抛物线经过A,C,D三点,且三点坐标为
A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(1)B点的坐标为
;
(2)是否存在F点,使四边形DFBG为矩形,
如存在求出F点坐标,如不存在,说明理由
2.
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),
D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,
且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,
设运动时间为t秒.
(1)填空:点A坐标为______;抛物线的解析式为______
.
(2)在图中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,
同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在(2)的条件下,当t为何值时,D.Q.P三点共线?
四小结
通过这节课的复习,你又增加了哪些收获?能与大家一起分享吗?
A
C
D
O
P
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
