苏科版九下数学 7.3特殊角的三角函数教案
文档属性
| 名称 | 苏科版九下数学 7.3特殊角的三角函数教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 25.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 18:20:33 | ||
图片预览

文档简介
课
题
7.3特殊角的三角函数值
课时
课
型
新授
素养目标
1.能通过推理得30°、45°、60°角的三角函数值,进一步体会三角函数的意义;2.会计算含有30°、45°、60°角的三角函数值,能根据30°、45°、60°角的三角函数值,说出相应锐角的大小;3.经历探索30°、45°、60°角的三角函数值的过程,发展学生推理能力和计算能力.
教学重点
能结合几何图形求出30°、45°、60°角的三角函数值,并能运用计算求值.
教学难点
能结合几何图形求出30°、45°、60°角的三角函数值,并能运用计算求值.
教学方法
自主学习,思考交流.
课前预习
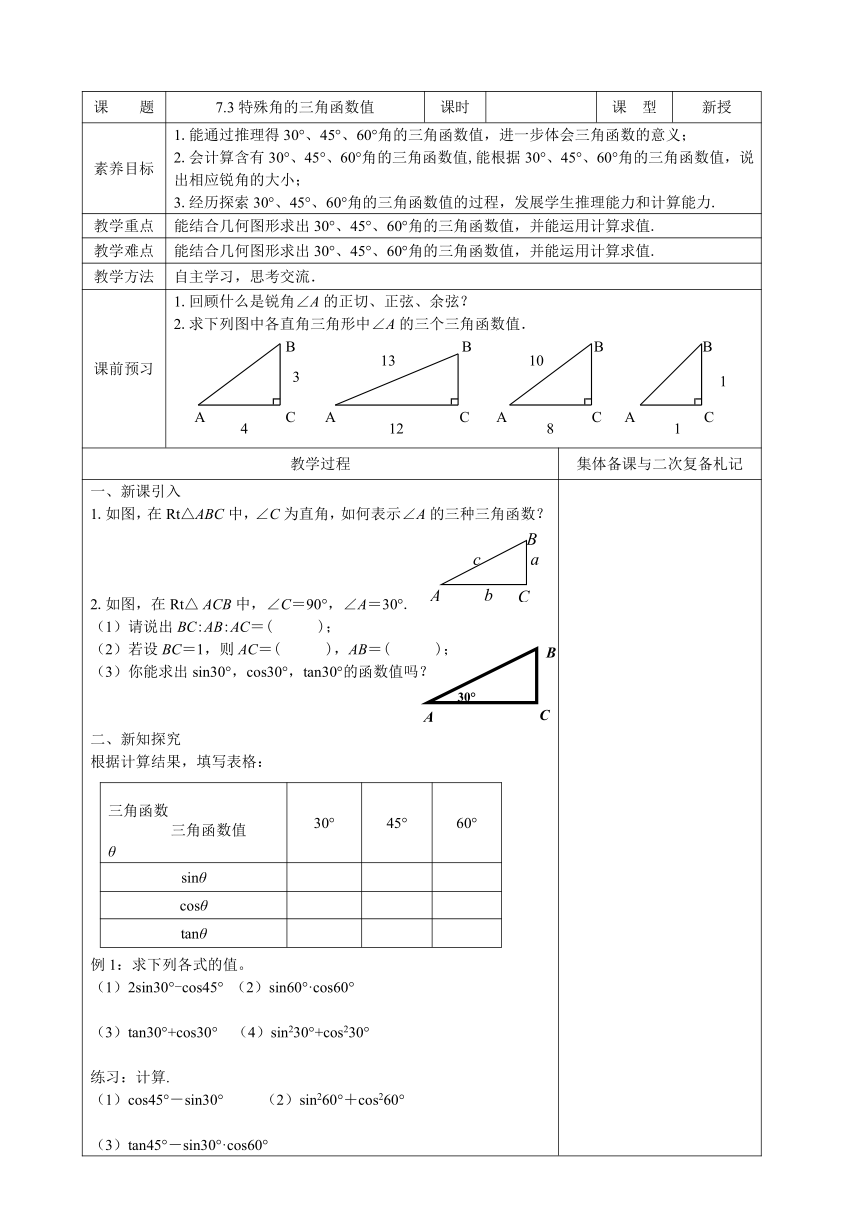
1.回顾什么是锐角∠A的正切、正弦、余弦?2.求下列图中各直角三角形中∠A的三个三角函数值.
教学过程
集体备课与二次复备札记
一、新课引入1.如图,在Rt△ABC中,∠C为直角,如何表示∠A的三种三角函数?2.如图,在Rt△
ACB中,∠C=90°,∠A=30°.(1)请说出BC:AB:AC=(
);(2)若设BC=1,则AC=(
),AB=(
);(3)你能求出sin30°,cos30°,tan30°的函数值吗?二、新知探究根据计算结果,填写表格:三角函数
三角函数值θ30°45°60°sinθcosθtanθ例1:求下列各式的值。(1)2sin30°-cos45°
(2)sin60°·cos60°
(3)tan30°+cos30°
(4)sin230°+cos230°练习:计算.(1)cos45°-sin30°
(2)sin260°+cos260°(3)tan45°-sin30°·cos60°
例2:求满足下列条件的锐角α:(1)cosα=
(2)2sinα=1
(3)2sinα-=0
(4)tanα-1=0例3:计算(1)
2sin30°-tan60°+cos45°;
(2)
sin260°+cos260°+tan45°.练习:(1)在△ABC中,∠A=75°,sinC=,则∠B=
;
(2)锐角α满足2sin(3α-15°)=1,则α为
;(3)已知α是锐角,且满足tan(α+20°)=3,则α=
°;(4)在△ABC中,若=0,则∠C=
°.三、拓展延伸:1.已知α为锐角,当无意义时,求tan(α+15°)-tan(α-15°)的值.2.已知△ABD中,AC是BD边上的高,AC=2,AB=2,AD=4,求∠BAD的度数.四、课堂小结1.你能说一说特殊角的三角函数有哪些求法吗?2.这节课你掌握了哪些数学方法?感受到什么数学思想?3.你还有什么收获或困惑吗?五、自主检测
教后反思
A
A
A
A
B
B
B
B
C
C
C
C
3
4
12
13
8
10
1
1
C
A
b
a
c
B
A
B
C
30°
题
7.3特殊角的三角函数值
课时
课
型
新授
素养目标
1.能通过推理得30°、45°、60°角的三角函数值,进一步体会三角函数的意义;2.会计算含有30°、45°、60°角的三角函数值,能根据30°、45°、60°角的三角函数值,说出相应锐角的大小;3.经历探索30°、45°、60°角的三角函数值的过程,发展学生推理能力和计算能力.
教学重点
能结合几何图形求出30°、45°、60°角的三角函数值,并能运用计算求值.
教学难点
能结合几何图形求出30°、45°、60°角的三角函数值,并能运用计算求值.
教学方法
自主学习,思考交流.
课前预习
1.回顾什么是锐角∠A的正切、正弦、余弦?2.求下列图中各直角三角形中∠A的三个三角函数值.
教学过程
集体备课与二次复备札记
一、新课引入1.如图,在Rt△ABC中,∠C为直角,如何表示∠A的三种三角函数?2.如图,在Rt△
ACB中,∠C=90°,∠A=30°.(1)请说出BC:AB:AC=(
);(2)若设BC=1,则AC=(
),AB=(
);(3)你能求出sin30°,cos30°,tan30°的函数值吗?二、新知探究根据计算结果,填写表格:三角函数
三角函数值θ30°45°60°sinθcosθtanθ例1:求下列各式的值。(1)2sin30°-cos45°
(2)sin60°·cos60°
(3)tan30°+cos30°
(4)sin230°+cos230°练习:计算.(1)cos45°-sin30°
(2)sin260°+cos260°(3)tan45°-sin30°·cos60°
例2:求满足下列条件的锐角α:(1)cosα=
(2)2sinα=1
(3)2sinα-=0
(4)tanα-1=0例3:计算(1)
2sin30°-tan60°+cos45°;
(2)
sin260°+cos260°+tan45°.练习:(1)在△ABC中,∠A=75°,sinC=,则∠B=
;
(2)锐角α满足2sin(3α-15°)=1,则α为
;(3)已知α是锐角,且满足tan(α+20°)=3,则α=
°;(4)在△ABC中,若=0,则∠C=
°.三、拓展延伸:1.已知α为锐角,当无意义时,求tan(α+15°)-tan(α-15°)的值.2.已知△ABD中,AC是BD边上的高,AC=2,AB=2,AD=4,求∠BAD的度数.四、课堂小结1.你能说一说特殊角的三角函数有哪些求法吗?2.这节课你掌握了哪些数学方法?感受到什么数学思想?3.你还有什么收获或困惑吗?五、自主检测
教后反思
A
A
A
A
B
B
B
B
C
C
C
C
3
4
12
13
8
10
1
1
C
A
b
a
c
B
A
B
C
30°
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
