人教版八年级数学下册第18章平行四边形章节测试(含答案)
文档属性
| 名称 | 人教版八年级数学下册第18章平行四边形章节测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-03 23:23:17 | ||
图片预览

文档简介
八年级数学下册
第十八章平行四边形
一、选择题
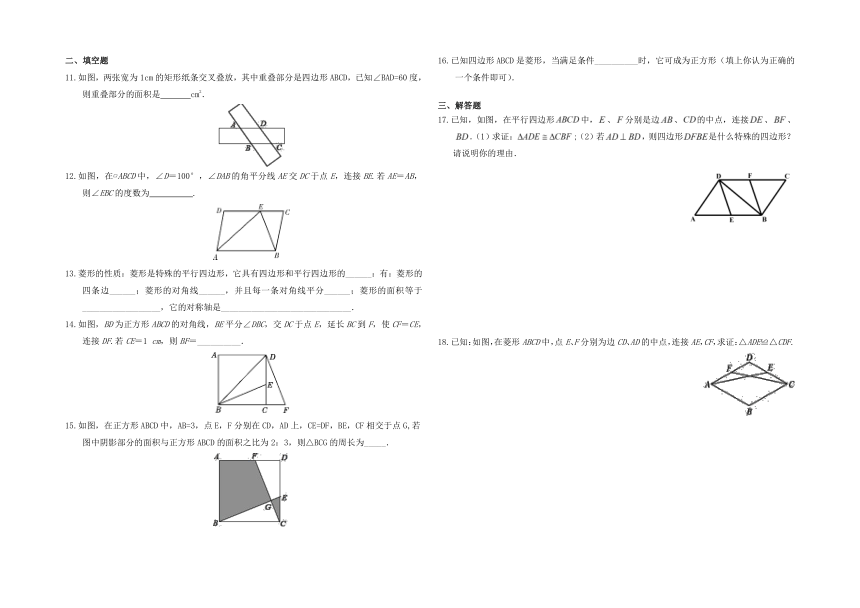
1.如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是(
)
A.
1<m<11
B.
2<m<22
C.
10<m<12
D.
5<m<6
2.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(
)
A.6
B.12
C.20
D.24
3.下列命题中,正确的是(
).
A.两邻边相等的四边形是菱形
B.一条对角线平分一个内角的平行四边形是菱形
C.对角线垂直且一组邻边相等的四边形是菱形
D.对角线垂直的四边形是菱形
4.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠ABC=75°,则∠EAF的度数为(
)
A.60°
B.65°
C.70°
D.75°
5.在?ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是(
)
A.AB=AD
B.OA=OB
C.AC=BD
D.DC⊥BC
6.如图,已知在菱形ABCD中,AE⊥BC于点E,若S菱形ABCD=24,且AE=6,则菱形的边长为
(
)
A.12
B.8
C.4
D.2
7.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB;
②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A.B、D、E构成的四边形是菱形,其中正确的是(
)
A.①④
B.①③④
C.①②③
D.②③④
8.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于(
)
A.75°
B.60°
C.45°
D.30°
9.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为(
).
A.4,4,8,8
B.5,5,7,7
C.5.5,5.5,6.5,6.5
D.3,3,9,9
10.如图,若平行四边形ABCD的周长是28
cm,△ABC的周长是22
cm,则AC的长为(
)
A.14
cm
B.12
cm
C.10
cm
D.8
cm
二、填空题
11.如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分是四边形ABCD,已知∠BAD=60度,则重叠部分的面积是
cm2.
12.如图,在?ABCD中,∠D=100°,∠DAB的角平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
13.菱形的性质:菱形是特殊的平行四边形,它具有四边形和平行四边形的______:有:菱形的四条边______;菱形的对角线______,并且每一条对角线平分______;菱形的面积等于__________________,它的对称轴是______________________________.
14.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1
cm,则BF=__________.
15.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.
16.已知四边形ABCD是菱形,当满足条件__________时,它可成为正方形(填上你认为正确的一个条件即可).
三、解答题
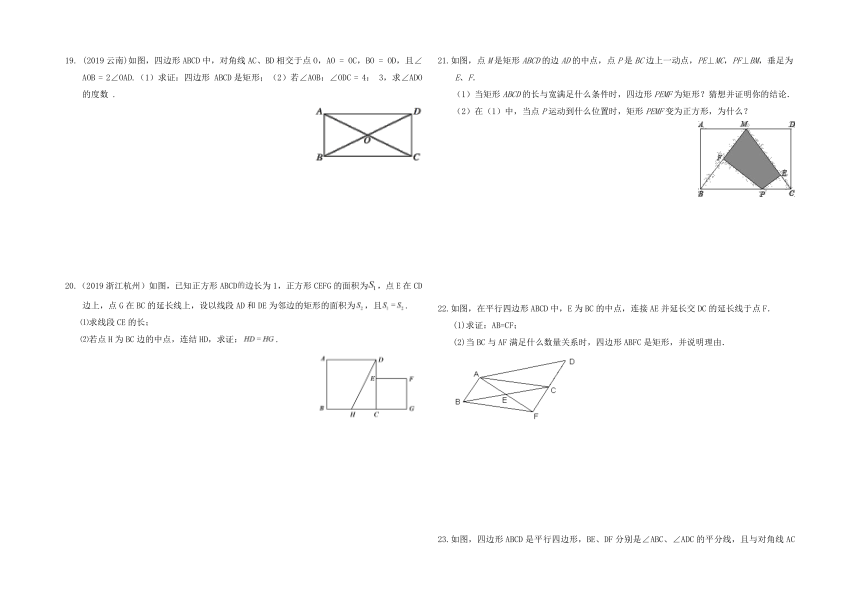
17.已知,如图,在平行四边形中,、分别是边、的中点,连接、、.(1)求证:;(2)若,则四边形是什么特殊的四边形?
请说明你的理由.
18.已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.
19.
(2019云南)如图,四边形ABCD中,对角线AC、BD相交于点O,AO
=
OC,BO
=
OD,且∠AOB
=
2∠OAD.(1)求证:四边形
ABCD是矩形;(2)若∠AOB:∠ODC
=
4:
3,求∠ADO的度数
.
20.(2019浙江杭州)如图,已知正方形ABCD边长为1,正方形CEFG的面积为,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:.
21.如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
22.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
23.如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.求证:AE=CF.
24.如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)试说明△BDE≌△CDF;
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
答案解析
1
2
3
4
5
6
7
8
9
10
A
D
B
D
A
C
A
B
B
D
11.
12.30°
13.所有性质,都相等;互相垂直,一组对角;底乘以高的一半或两条对角线之积的一半;对角线所在的直线.
14.
(2+)cm 点拨:过点E作EG⊥BD于点G.
∵BE平分∠DBC,∠EGB=∠BCE=90°,
∴EG=EC=1
cm.
易知△DEG为等腰直角三角形,
∴DE=EG=cm.∴CD=(1+)cm,那么BC=(1+)cm.又∵CF=CE=1
cm,
∴BF=(2+)cm.
15.+3.
16.答案不唯一,如:∠A=90°
17.(1)证明:∵四边形是平行四边形
∴
又∵、分别是边、的中点
∴
在和
∵
∴
(2)四边形是菱形,理由如下:
∵且
∴四边形是平行四边形
又∵且是的中点
∴
∴平行四边形是菱形.
18.【答案】证明∵四边形ABCD是菱形,
∴AD=CD,
∵点E、F分别为边CD、AD的中点,
∴AD=2DF,CD=2DE,
∴DE=DF,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS).
【解析】由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由SAS证明△ADE≌△CDF即可.
19.
(1)
证明:∵AO
=
OC,
BO
=
OD,
∴四边形
ABCD是平行四边形.
∵∠AOB
=
2∠OAD,∠AOB
=
∠OAD∠+
ODA,
∴∠OAD
=∠ODA.
∴AO
=
DO.
∴AO
=
OC
=
BO
=
OD,
∴AC
=
BD.
∴四边形ABCD是矩形.
(2)
设∠AOB
=
4
x°,∠ODC
=
3x°,则∠COD
=
4x°,∠OCD
=
3x°.
在△COD中,∠COD
+∠OCD
+∠ODC
=
180°,
∴4x
+
3
x
+
3
x
=
180
,
解得
x
=
18
,∴∠ODC
=
3x°
=
54°,
∴∠ADO
=
90°
-
∠ODC
=
90°
–
54°
=
36
°.
20.【答案】(1)CE=;(2)见解析.
【详解】根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0因为S1=S2,所以x2=1-x,
解得x=(负根舍去),
即CE=
(2)因为点H为BC边的中点,
所以CH=,所以HD=,
因为CG=CE=,点H,C,G在同一直线上,
所以HG=HC+CG=+=,所以HD=HG
【点睛】本题考查正方形的性质、勾股定理和一元二次函数,解题的关键是根据题意列出一元二次函数.
21.【分析】(1)根据矩形的性质推出∠A=∠D=90°,AB=CD,AM=DM,求出∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,求出∠BMC,即可求出矩形PEMF.
(2)根据AAS证△BFP≌△CEP,推出PE=PF即可.
【解答】(1)解:当AD=2AB时,四边形PEMF为矩形.
证明:∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵AD=2AB=2CD,AM=DM=AD,
∴AB=AM=DM=CD,
∴∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,
∴∠BMC=180°﹣45°﹣45°=90°,
∵PE⊥MC,PF⊥BM,
∴∠MEP=∠FPE=90°,
∴四边形PEMF为矩形,
即当AD=2AB时,四边形PEMF为矩形.
(2)解:当P是BC的中点时,矩形PEMF为正方形.
理由是:∵四边形PEMF为矩形,
∴∠PFM=∠PFB=∠PEC=90°,
在△BFP和△CEP中
,
∴△BFP≌△CEP(AAS),
∴PE=PF,
∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当P是BC的中点时,矩形PEMF为正方形.
【点评】本题主要考查对矩形的判定和性质,正方形的判定,等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.
22.(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴,
∵E为BC的中点
∴BE=EC
∴
△ABE≌△FCE
∴
AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.理由如下:
∵AB∥CF,AB=CF
∴四边形ABFC是平行四边形
∵BC=AF
∴四边形ABFC是矩形.
23.证明:因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,∠ABC=∠ADC,
所以∠BAC=∠DCF,
又因为BE、DF分别是∠ABC、∠ADC的平分线,
所以∠ABE=∠ABC,∠CDF=∠ADC,
所以∠ABE=∠CDF,
所以△ABE≌△CDF(ASA),
所以AE=CF.
24.解:(1)∵CF∥BE,
∴∠FCD=∠EBD.
∵D是BC的中点,
∴CD=BD.
∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
(2)四边形BECF是平行四边形.
理由:∵△CDF≌△BDE,
∴DF=DE,DC=DB.
∴四边形BECF是平行四边形.
第十八章平行四边形
一、选择题
1.如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是(
)
A.
1<m<11
B.
2<m<22
C.
10<m<12
D.
5<m<6
2.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(
)
A.6
B.12
C.20
D.24
3.下列命题中,正确的是(
).
A.两邻边相等的四边形是菱形
B.一条对角线平分一个内角的平行四边形是菱形
C.对角线垂直且一组邻边相等的四边形是菱形
D.对角线垂直的四边形是菱形
4.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠ABC=75°,则∠EAF的度数为(
)
A.60°
B.65°
C.70°
D.75°
5.在?ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是(
)
A.AB=AD
B.OA=OB
C.AC=BD
D.DC⊥BC
6.如图,已知在菱形ABCD中,AE⊥BC于点E,若S菱形ABCD=24,且AE=6,则菱形的边长为
(
)
A.12
B.8
C.4
D.2
7.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB;
②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A.B、D、E构成的四边形是菱形,其中正确的是(
)
A.①④
B.①③④
C.①②③
D.②③④
8.在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于(
)
A.75°
B.60°
C.45°
D.30°
9.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为(
).
A.4,4,8,8
B.5,5,7,7
C.5.5,5.5,6.5,6.5
D.3,3,9,9
10.如图,若平行四边形ABCD的周长是28
cm,△ABC的周长是22
cm,则AC的长为(
)
A.14
cm
B.12
cm
C.10
cm
D.8
cm
二、填空题
11.如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分是四边形ABCD,已知∠BAD=60度,则重叠部分的面积是
cm2.
12.如图,在?ABCD中,∠D=100°,∠DAB的角平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为
.
13.菱形的性质:菱形是特殊的平行四边形,它具有四边形和平行四边形的______:有:菱形的四条边______;菱形的对角线______,并且每一条对角线平分______;菱形的面积等于__________________,它的对称轴是______________________________.
14.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1
cm,则BF=__________.
15.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.
16.已知四边形ABCD是菱形,当满足条件__________时,它可成为正方形(填上你认为正确的一个条件即可).
三、解答题
17.已知,如图,在平行四边形中,、分别是边、的中点,连接、、.(1)求证:;(2)若,则四边形是什么特殊的四边形?
请说明你的理由.
18.已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.
19.
(2019云南)如图,四边形ABCD中,对角线AC、BD相交于点O,AO
=
OC,BO
=
OD,且∠AOB
=
2∠OAD.(1)求证:四边形
ABCD是矩形;(2)若∠AOB:∠ODC
=
4:
3,求∠ADO的度数
.
20.(2019浙江杭州)如图,已知正方形ABCD边长为1,正方形CEFG的面积为,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:.
21.如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
22.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
23.如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.求证:AE=CF.
24.如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)试说明△BDE≌△CDF;
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
答案解析
1
2
3
4
5
6
7
8
9
10
A
D
B
D
A
C
A
B
B
D
11.
12.30°
13.所有性质,都相等;互相垂直,一组对角;底乘以高的一半或两条对角线之积的一半;对角线所在的直线.
14.
(2+)cm 点拨:过点E作EG⊥BD于点G.
∵BE平分∠DBC,∠EGB=∠BCE=90°,
∴EG=EC=1
cm.
易知△DEG为等腰直角三角形,
∴DE=EG=cm.∴CD=(1+)cm,那么BC=(1+)cm.又∵CF=CE=1
cm,
∴BF=(2+)cm.
15.+3.
16.答案不唯一,如:∠A=90°
17.(1)证明:∵四边形是平行四边形
∴
又∵、分别是边、的中点
∴
在和
∵
∴
(2)四边形是菱形,理由如下:
∵且
∴四边形是平行四边形
又∵且是的中点
∴
∴平行四边形是菱形.
18.【答案】证明∵四边形ABCD是菱形,
∴AD=CD,
∵点E、F分别为边CD、AD的中点,
∴AD=2DF,CD=2DE,
∴DE=DF,
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS).
【解析】由菱形的性质得出AD=CD,由中点的定义证出DE=DF,由SAS证明△ADE≌△CDF即可.
19.
(1)
证明:∵AO
=
OC,
BO
=
OD,
∴四边形
ABCD是平行四边形.
∵∠AOB
=
2∠OAD,∠AOB
=
∠OAD∠+
ODA,
∴∠OAD
=∠ODA.
∴AO
=
DO.
∴AO
=
OC
=
BO
=
OD,
∴AC
=
BD.
∴四边形ABCD是矩形.
(2)
设∠AOB
=
4
x°,∠ODC
=
3x°,则∠COD
=
4x°,∠OCD
=
3x°.
在△COD中,∠COD
+∠OCD
+∠ODC
=
180°,
∴4x
+
3
x
+
3
x
=
180
,
解得
x
=
18
,∴∠ODC
=
3x°
=
54°,
∴∠ADO
=
90°
-
∠ODC
=
90°
–
54°
=
36
°.
20.【答案】(1)CE=;(2)见解析.
【详解】根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0
解得x=(负根舍去),
即CE=
(2)因为点H为BC边的中点,
所以CH=,所以HD=,
因为CG=CE=,点H,C,G在同一直线上,
所以HG=HC+CG=+=,所以HD=HG
【点睛】本题考查正方形的性质、勾股定理和一元二次函数,解题的关键是根据题意列出一元二次函数.
21.【分析】(1)根据矩形的性质推出∠A=∠D=90°,AB=CD,AM=DM,求出∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,求出∠BMC,即可求出矩形PEMF.
(2)根据AAS证△BFP≌△CEP,推出PE=PF即可.
【解答】(1)解:当AD=2AB时,四边形PEMF为矩形.
证明:∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵AD=2AB=2CD,AM=DM=AD,
∴AB=AM=DM=CD,
∴∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,
∴∠BMC=180°﹣45°﹣45°=90°,
∵PE⊥MC,PF⊥BM,
∴∠MEP=∠FPE=90°,
∴四边形PEMF为矩形,
即当AD=2AB时,四边形PEMF为矩形.
(2)解:当P是BC的中点时,矩形PEMF为正方形.
理由是:∵四边形PEMF为矩形,
∴∠PFM=∠PFB=∠PEC=90°,
在△BFP和△CEP中
,
∴△BFP≌△CEP(AAS),
∴PE=PF,
∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当P是BC的中点时,矩形PEMF为正方形.
【点评】本题主要考查对矩形的判定和性质,正方形的判定,等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.
22.(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴,
∵E为BC的中点
∴BE=EC
∴
△ABE≌△FCE
∴
AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.理由如下:
∵AB∥CF,AB=CF
∴四边形ABFC是平行四边形
∵BC=AF
∴四边形ABFC是矩形.
23.证明:因为四边形ABCD是平行四边形,
所以AB=CD,AB∥CD,∠ABC=∠ADC,
所以∠BAC=∠DCF,
又因为BE、DF分别是∠ABC、∠ADC的平分线,
所以∠ABE=∠ABC,∠CDF=∠ADC,
所以∠ABE=∠CDF,
所以△ABE≌△CDF(ASA),
所以AE=CF.
24.解:(1)∵CF∥BE,
∴∠FCD=∠EBD.
∵D是BC的中点,
∴CD=BD.
∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
(2)四边形BECF是平行四边形.
理由:∵△CDF≌△BDE,
∴DF=DE,DC=DB.
∴四边形BECF是平行四边形.
