人教版八年级数学 下册期末提优测试:第二十章 数据的分析(含答案)
文档属性
| 名称 | 人教版八年级数学 下册期末提优测试:第二十章 数据的分析(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 05:51:46 | ||
图片预览



文档简介
第二十章
数据的分析
1.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是(
)
A.255分
B.84分
C.84.5分
D.86分
2.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
3.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是( )
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
4.若数据m,2,5,7,1,4,n的平均数为4,则m,n的平均数为(
)
(A)7.5
(B)5.5
(C)2.5
(D)4.5
5.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较(
)
A.变大
B.变小
C.相等
D.无法确定
6.为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm)为:16 9 14 11 12 10 16 8 17 19,则这组数据的中位数和极差分别是
A.?13,16????????????????????????????B.?14,11???????????????????????????
C.?12,11????????????????????????????D.?13,11
7.在某中学举行的演讲比赛中,八年级5名参赛选手的成绩如下表所示,你根据表中提供的数据,计算出这5名选手成绩的方差为(
)
A.2
B.6.8
C.34
D.93
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为(
)
A.76
B.75
C.74
D.73
9.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.?79.25分???????????????????????????B.?80.75分???????????????????????????
C.?81.06分???????????????????????????D.?82.53分
10.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是( )
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
11.一组数据共4个数,其平均数为5,极差是6,则下列满足条件的一组数据是(???).
A.?0,8,6,6????????????????????????????B.?1,5,5,7?????????????????????????????
C.?1,7,6,6?????????????????????????????D.?3,5,6,6
12.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
.?
13.如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是________.
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
15.一组数据按从小到大的顺序排列为1,2,3,x,4,5,若这组数据的平均数为3,则x的值是________.
16.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
17.小明等五名同学四月份参加某次数学测验的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为________
.
18.某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2015﹣2019这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
2015
2016
2017
2018
2019
234
233
245
247
256
(1)这五年的全年空气质量优良天数的中位数是________,平均数是________;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是________年(填写年份);
(3)求这五年的全年空气质量优良天数的方差________.
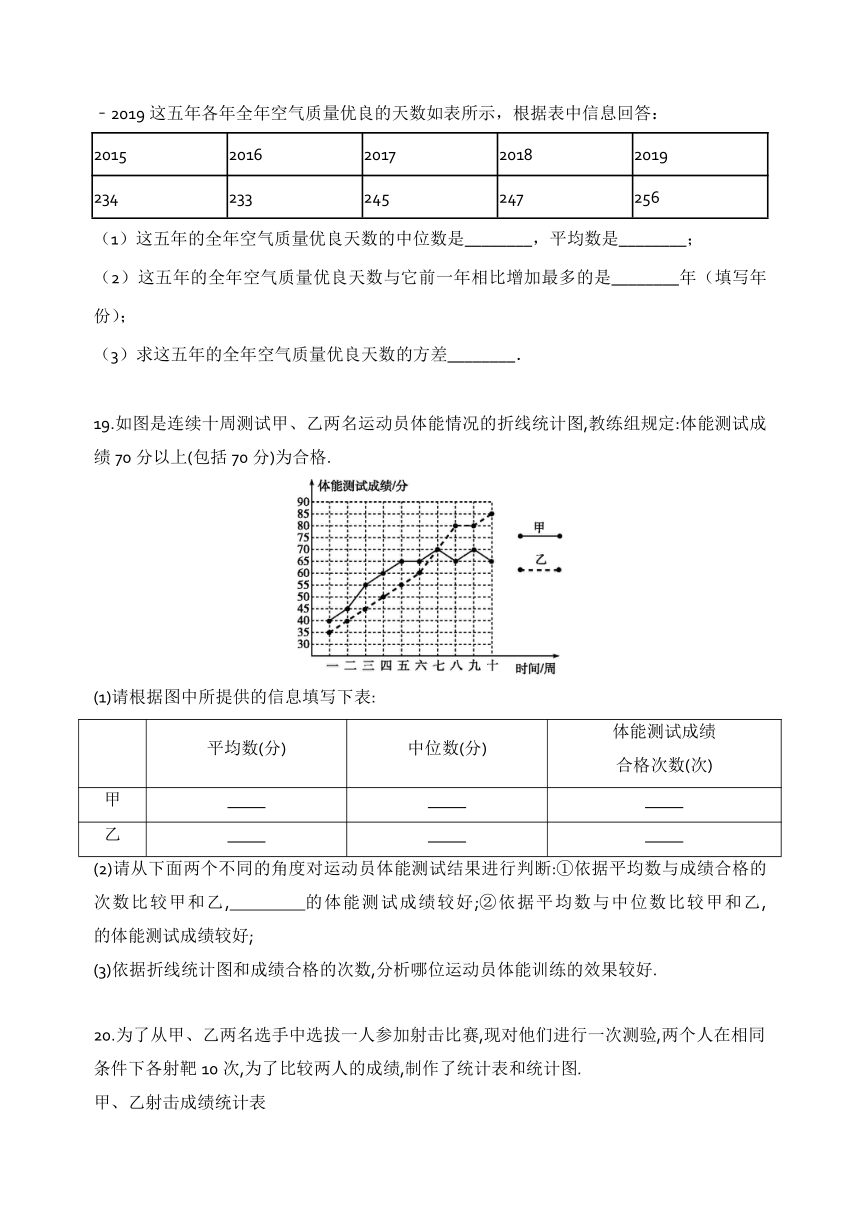
19.如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合格.
(1)请根据图中所提供的信息填写下表:
平均数(分)
中位数(分)
体能测试成绩合格次数(次)
甲
?
?
?
乙
?
?
?
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙, 的体能测试成绩较好;②依据平均数与中位数比较甲和乙,
的体能测试成绩较好;?
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
21.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
22.某市为了节约生活用水,计划制定每位居民统一的月用水量标准,然后根据标准,实行分段收费.为此,对居民上年度的月均用水量进行了抽样调查,并根据调查结果绘制了上年度月均用水量的频数分布直方图(图中分组含最低值,不含最高值),请根据图中信息解答下列问题:
(1)本次调查的居民人数为 ;?
(2)本次调查的居民月均用水量的中位数落在频数分布直方图中的第 小组内(从左至右数);?
(3)当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准,根据上述调查结果,你认为月用水量标准(取整数)定为多少吨时较为合适?
23.某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号
1
2
3
4
5
6
7
8
9
10
打分
7.0
7.8
3.2
8.0
8.4
8.4
9.8
8.0
8.4
8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
答案
1.
D
2.
D
3.
C
4.
D
5.
B
6.
D
7.
B
8.
A
9.
C
10.
A
11.
C
12.
82
13.
7
14.
183
15.
3
16.
350
17.
60或110
18.
245;243;2012;74
19.
解:(1)填表如下
平均数(分)
中位数(分)
体能测试成绩合格次数(次)
甲
60 ?
65 ?
2 ?
乙
60 ?
57.5 ?
4 ?
(2)乙 甲
(3)从折线图上看,两名运动员体能测试成绩都呈上升的趋势,但是,乙的增长速度比甲快,并且后一阶段乙的成绩合格的次数比甲多,所以乙训练的效果较好.
20.
解
(1)根据折线统计图得乙的射击成绩为2,4,6,7,7,8,8,9,9,10,则平均数为=7,中位数为7.5,方差为×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
7
1.6
0
乙
7
7.5
5.4
1
甲、乙射击成绩折线图
(2)因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,所以甲胜出.
(3)希望乙胜出,规则为命中9环与10环的总数大的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.
21.
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
22.
解
(1)100
(2)5(或五)
(3)居民月用水量标准定为3吨较为合适.
23.
解:(1)方案一最后得分:(7.0+7.8+3.2+3×8+3×8.4+9.8)=7.7;
方案二最后得分:(7.0+7.8+3×8+3×8.4)=8;
方案三最后得分:8;
方案四最后得分:8和8.4.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案;
数据的分析
1.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是(
)
A.255分
B.84分
C.84.5分
D.86分
2.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
3.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是( )
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
4.若数据m,2,5,7,1,4,n的平均数为4,则m,n的平均数为(
)
(A)7.5
(B)5.5
(C)2.5
(D)4.5
5.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较(
)
A.变大
B.变小
C.相等
D.无法确定
6.为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm)为:16 9 14 11 12 10 16 8 17 19,则这组数据的中位数和极差分别是
A.?13,16????????????????????????????B.?14,11???????????????????????????
C.?12,11????????????????????????????D.?13,11
7.在某中学举行的演讲比赛中,八年级5名参赛选手的成绩如下表所示,你根据表中提供的数据,计算出这5名选手成绩的方差为(
)
A.2
B.6.8
C.34
D.93
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为(
)
A.76
B.75
C.74
D.73
9.某年级有四个班,人数分别为:一班25人,二班22人,三班27人,四班26人.在一次考试中,四个班的班级平均分依次为81分,75分,89分,78分,则这次考试的年级平均分为( )
A.?79.25分???????????????????????????B.?80.75分???????????????????????????
C.?81.06分???????????????????????????D.?82.53分
10.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是( )
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
11.一组数据共4个数,其平均数为5,极差是6,则下列满足条件的一组数据是(???).
A.?0,8,6,6????????????????????????????B.?1,5,5,7?????????????????????????????
C.?1,7,6,6?????????????????????????????D.?3,5,6,6
12.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
.?
13.如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是________.
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
15.一组数据按从小到大的顺序排列为1,2,3,x,4,5,若这组数据的平均数为3,则x的值是________.
16.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
17.小明等五名同学四月份参加某次数学测验的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为________
.
18.某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2015﹣2019这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
2015
2016
2017
2018
2019
234
233
245
247
256
(1)这五年的全年空气质量优良天数的中位数是________,平均数是________;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是________年(填写年份);
(3)求这五年的全年空气质量优良天数的方差________.
19.如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合格.
(1)请根据图中所提供的信息填写下表:
平均数(分)
中位数(分)
体能测试成绩合格次数(次)
甲
?
?
?
乙
?
?
?
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙, 的体能测试成绩较好;②依据平均数与中位数比较甲和乙,
的体能测试成绩较好;?
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
21.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
22.某市为了节约生活用水,计划制定每位居民统一的月用水量标准,然后根据标准,实行分段收费.为此,对居民上年度的月均用水量进行了抽样调查,并根据调查结果绘制了上年度月均用水量的频数分布直方图(图中分组含最低值,不含最高值),请根据图中信息解答下列问题:
(1)本次调查的居民人数为 ;?
(2)本次调查的居民月均用水量的中位数落在频数分布直方图中的第 小组内(从左至右数);?
(3)当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准,根据上述调查结果,你认为月用水量标准(取整数)定为多少吨时较为合适?
23.某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号
1
2
3
4
5
6
7
8
9
10
打分
7.0
7.8
3.2
8.0
8.4
8.4
9.8
8.0
8.4
8.0
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
答案
1.
D
2.
D
3.
C
4.
D
5.
B
6.
D
7.
B
8.
A
9.
C
10.
A
11.
C
12.
82
13.
7
14.
183
15.
3
16.
350
17.
60或110
18.
245;243;2012;74
19.
解:(1)填表如下
平均数(分)
中位数(分)
体能测试成绩合格次数(次)
甲
60 ?
65 ?
2 ?
乙
60 ?
57.5 ?
4 ?
(2)乙 甲
(3)从折线图上看,两名运动员体能测试成绩都呈上升的趋势,但是,乙的增长速度比甲快,并且后一阶段乙的成绩合格的次数比甲多,所以乙训练的效果较好.
20.
解
(1)根据折线统计图得乙的射击成绩为2,4,6,7,7,8,8,9,9,10,则平均数为=7,中位数为7.5,方差为×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
7
1.6
0
乙
7
7.5
5.4
1
甲、乙射击成绩折线图
(2)因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,所以甲胜出.
(3)希望乙胜出,规则为命中9环与10环的总数大的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.
21.
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
22.
解
(1)100
(2)5(或五)
(3)居民月用水量标准定为3吨较为合适.
23.
解:(1)方案一最后得分:(7.0+7.8+3.2+3×8+3×8.4+9.8)=7.7;
方案二最后得分:(7.0+7.8+3×8+3×8.4)=8;
方案三最后得分:8;
方案四最后得分:8和8.4.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案;
