第18章 平行四边形 2020年春人教版八年级数学下册期末培优测试(含答案)
文档属性
| 名称 | 第18章 平行四边形 2020年春人教版八年级数学下册期末培优测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 15:02:17 | ||
图片预览

文档简介
十八章
平行四边形
1.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( )
(A)20
(B)24
(C)40
(D)48
2.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F.在下列结论中,不一定正确的是(
)
A.△AFD≌△DCE
B.AF=AD
C.AB=AF
D.BE=AD-DF
3.在ABCD中,∠A=5∠B,则∠C的度数是( )
(A)30°
(B)60°
(C)120°
(D)150°
4.如图,在?ABCD中,已知∠ODA=90°,AC=10
cm,BD=6
cm,则AD的长为(
)
A.4
cm
B.5
cm
C.6
cm
D.8
cm
5.如图,矩形ABCD的对角线AC和BD相交于点O,若∠AOD=120°,AC=10,则AB的长为( )
A.10
B.8
C.6
D.5
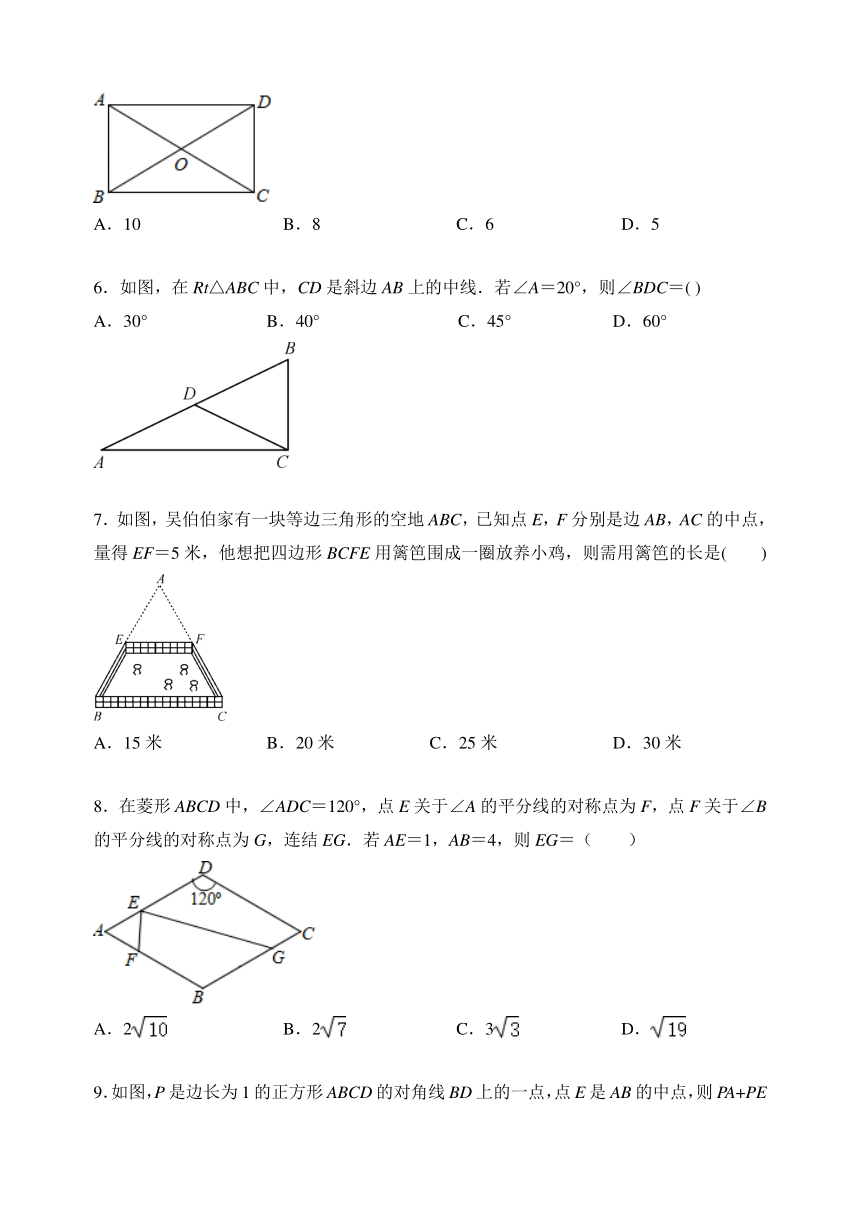
6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=(
)
A.30°
B.40°
C.45°
D.60°
7.如图,吴伯伯家有一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需用篱笆的长是(
)
A.15米
B.20米
C.25米
D.30米
8.在菱形ABCD中,∠ADC=120°,点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,连结EG.若AE=1,AB=4,则EG=( )
A.2
B.2
C.3
D.
9.如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
A.
B.
C.
D.
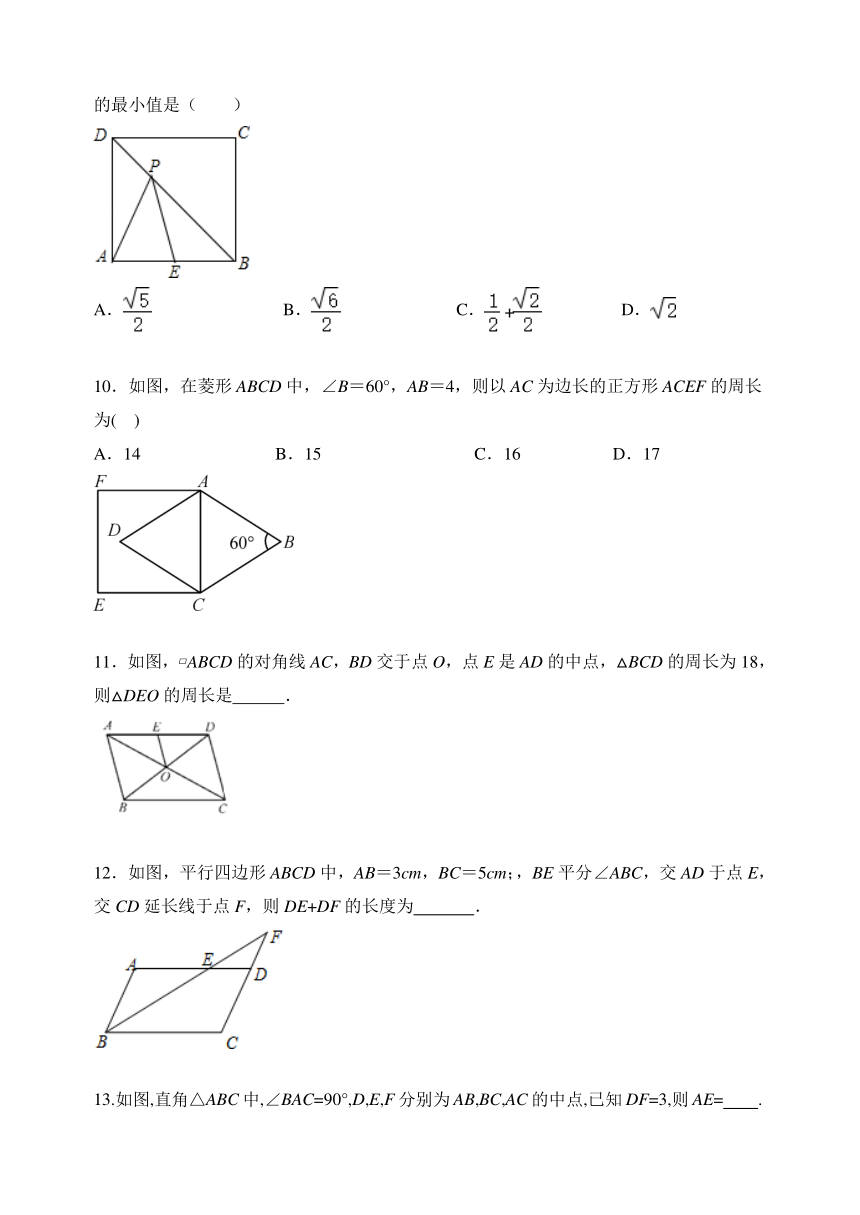
10.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为(
)
A.14
B.15
C.16
D.17
11.如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是
.
12.如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
.
13.如图,直角△ABC中,∠BAC=90°,D,E,F分别为AB,BC,AC的中点,已知DF=3,则AE= .?
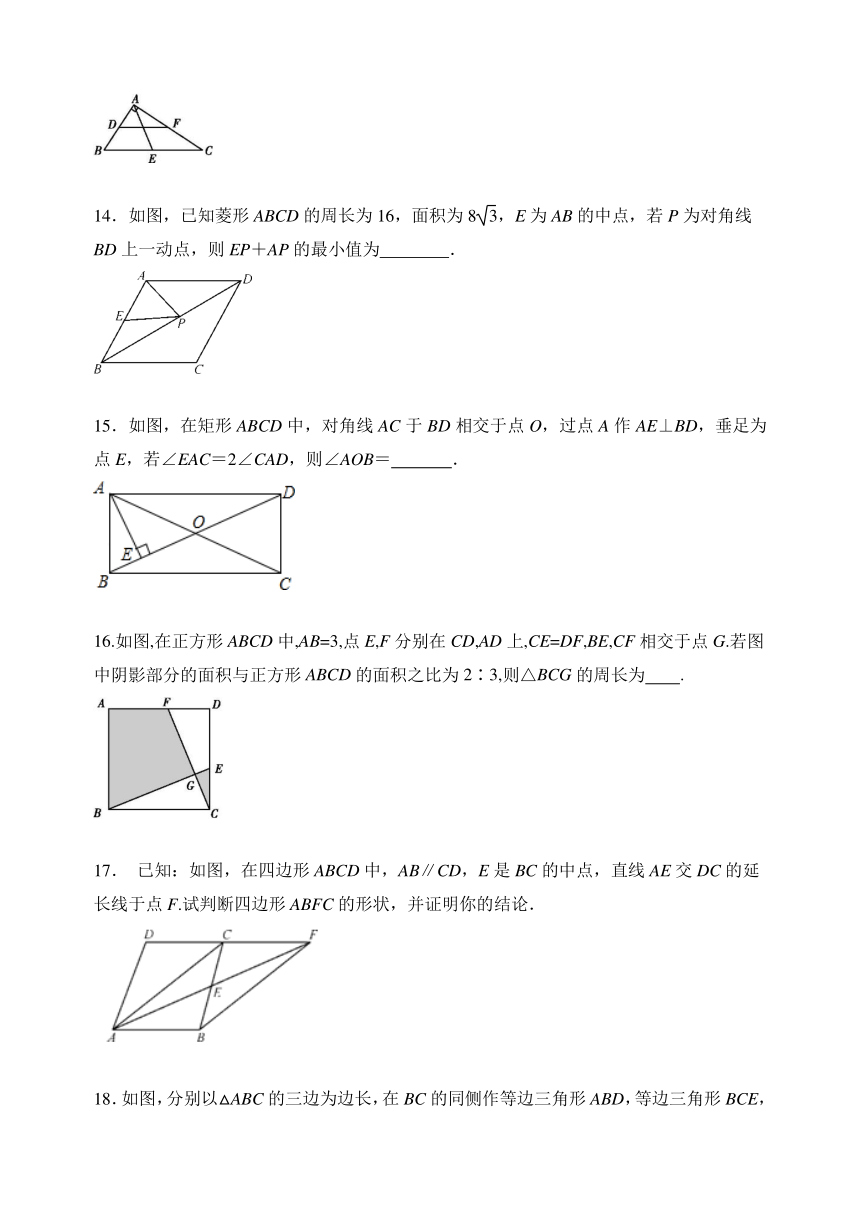
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为
.
15.如图,在矩形ABCD中,对角线AC于BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠AOB=
.
16.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为 .?
17.
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
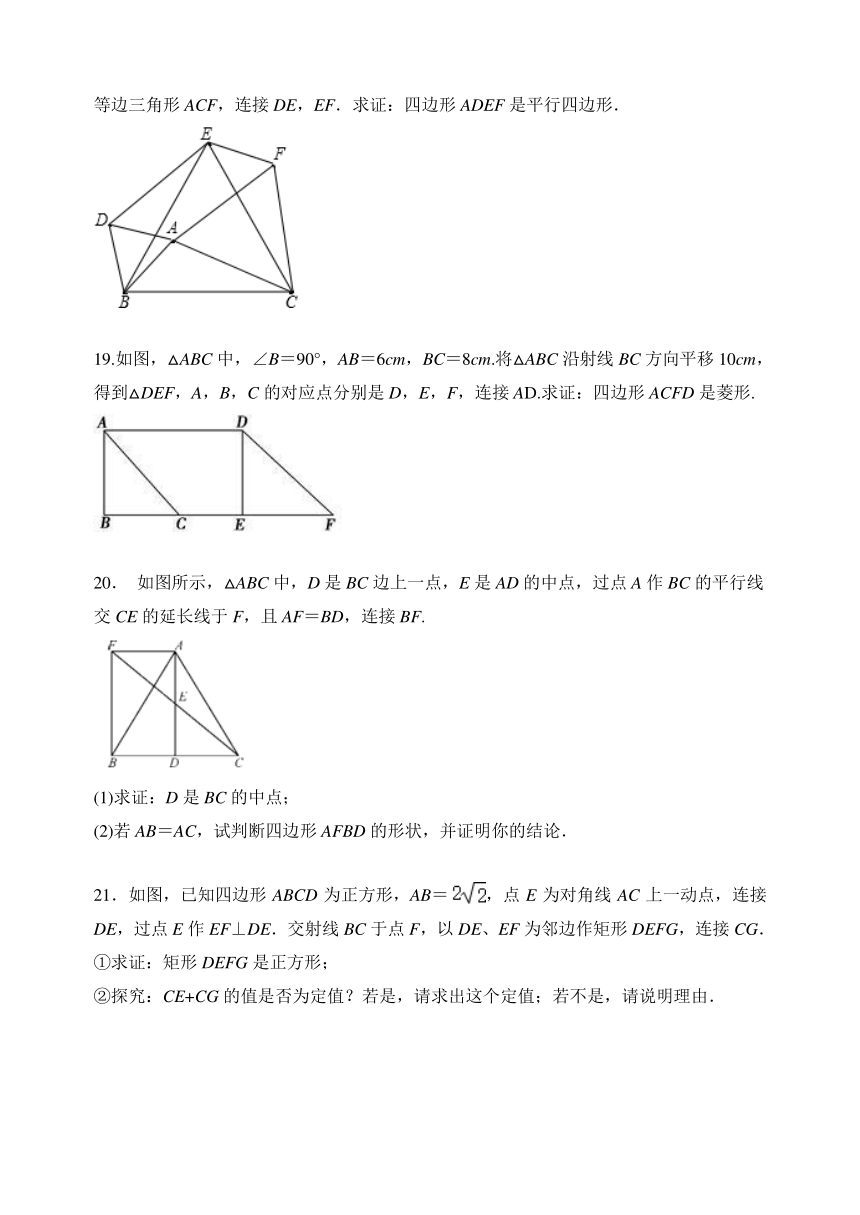
18.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
19.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
20.
如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
21.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
22.如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24
cm,BC=26
cm,点P从点A出发,以1
cm/s的速度向点D运动,同时点Q从点C出发,以3
cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为t
s.
(1)当t= s时,四边形APQB为矩形;?
(2)当四边形PQCD为平行四边形时,求t的值.
参考答案
1.
A
2.
B
3.
D
4.
A
5.
D
6.
B
7.
C
8.
B
9.
A
10.
C
11.
9
12.
4cm
13.
3
14.
2
15.
45°
16.
+3
17.
解:四边形ABFC是平行四边形.
证明:∵AB∥CD,
∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS).∴AB=CF.
又∵AB∥CF,∴四边形ABFC是平行四边形.
18.
证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE﹣∠ACE=∠ACF﹣∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
19.
证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴AC===10,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形.
20.
解:(1)证明:∵AF∥BC,
∴∠AFC=∠FCB.
又∵∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC(AAS).∴AF=DC.
又∵AF=BD,∴BD=DC,即D是BC的中点.
(2)四边形AFBD是矩形.
证明:∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADB=90°.
∴四边形AFBD是矩形.
21.
①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
②解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE=AB=×2=4,
∴CE+CG=4
是定值.
22.
解:(1)根据题意得AP=t
cm,CQ=3t
cm,
∵AD=24
cm,BC=26
cm,
∴BQ=(26-3t)
cm,
∵AD∥BC,∠B=90°,
∴当AP=BQ时,
四边形APQB是矩形,
∴t=26-3t,
解得t=6.5,
即当t=6.5
s时,
四边形APQB是矩形.
故答案为6.5.
(2)因为PD=(24-t)
cm,
CQ=3t
cm,
所以当PD=CQ时,
四边形PQCD为平行四边形,
即24-t=3t,
解得t=6.
所以当四边形PQCD为平行四边形时,t的值为6.
平行四边形
1.如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( )
(A)20
(B)24
(C)40
(D)48
2.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F.在下列结论中,不一定正确的是(
)
A.△AFD≌△DCE
B.AF=AD
C.AB=AF
D.BE=AD-DF
3.在ABCD中,∠A=5∠B,则∠C的度数是( )
(A)30°
(B)60°
(C)120°
(D)150°
4.如图,在?ABCD中,已知∠ODA=90°,AC=10
cm,BD=6
cm,则AD的长为(
)
A.4
cm
B.5
cm
C.6
cm
D.8
cm
5.如图,矩形ABCD的对角线AC和BD相交于点O,若∠AOD=120°,AC=10,则AB的长为( )
A.10
B.8
C.6
D.5
6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=(
)
A.30°
B.40°
C.45°
D.60°
7.如图,吴伯伯家有一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需用篱笆的长是(
)
A.15米
B.20米
C.25米
D.30米
8.在菱形ABCD中,∠ADC=120°,点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,连结EG.若AE=1,AB=4,则EG=( )
A.2
B.2
C.3
D.
9.如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
A.
B.
C.
D.
10.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为(
)
A.14
B.15
C.16
D.17
11.如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是
.
12.如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为
.
13.如图,直角△ABC中,∠BAC=90°,D,E,F分别为AB,BC,AC的中点,已知DF=3,则AE= .?
14.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为
.
15.如图,在矩形ABCD中,对角线AC于BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠AOB=
.
16.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为 .?
17.
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
18.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
19.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
20.
如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
21.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
22.如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24
cm,BC=26
cm,点P从点A出发,以1
cm/s的速度向点D运动,同时点Q从点C出发,以3
cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为t
s.
(1)当t= s时,四边形APQB为矩形;?
(2)当四边形PQCD为平行四边形时,求t的值.
参考答案
1.
A
2.
B
3.
D
4.
A
5.
D
6.
B
7.
C
8.
B
9.
A
10.
C
11.
9
12.
4cm
13.
3
14.
2
15.
45°
16.
+3
17.
解:四边形ABFC是平行四边形.
证明:∵AB∥CD,
∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS).∴AB=CF.
又∵AB∥CF,∴四边形ABFC是平行四边形.
18.
证明:∵△BCE、△ACF、△ABD都是等边三角形,
∴AB=AD,AC=CF,BC=CE,∠BCE=∠ACF,
∴∠BCE﹣∠ACE=∠ACF﹣∠ACE,
即∠BCA=∠FCE,
在△BCA和△ECF中,
,
∴△BCA≌△ECF(SAS),
∴AB=EF,
∵AB=AD,
∴AD=EF,
同理DE=AF,
∴四边形ADEF是平行四边形.
19.
证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴AC===10,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形.
20.
解:(1)证明:∵AF∥BC,
∴∠AFC=∠FCB.
又∵∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC(AAS).∴AF=DC.
又∵AF=BD,∴BD=DC,即D是BC的中点.
(2)四边形AFBD是矩形.
证明:∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADB=90°.
∴四边形AFBD是矩形.
21.
①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
②解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE=AB=×2=4,
∴CE+CG=4
是定值.
22.
解:(1)根据题意得AP=t
cm,CQ=3t
cm,
∵AD=24
cm,BC=26
cm,
∴BQ=(26-3t)
cm,
∵AD∥BC,∠B=90°,
∴当AP=BQ时,
四边形APQB是矩形,
∴t=26-3t,
解得t=6.5,
即当t=6.5
s时,
四边形APQB是矩形.
故答案为6.5.
(2)因为PD=(24-t)
cm,
CQ=3t
cm,
所以当PD=CQ时,
四边形PQCD为平行四边形,
即24-t=3t,
解得t=6.
所以当四边形PQCD为平行四边形时,t的值为6.
