11.1.2 三角形的高、中线与角平分线课件(共28张PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 16:08:08 | ||
图片预览



文档简介
(共28张PPT)
人教版
八年级数学上
11.1.2
三角形的高、中线与角平分线
学习目标
1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
回顾旧知
l
A
B
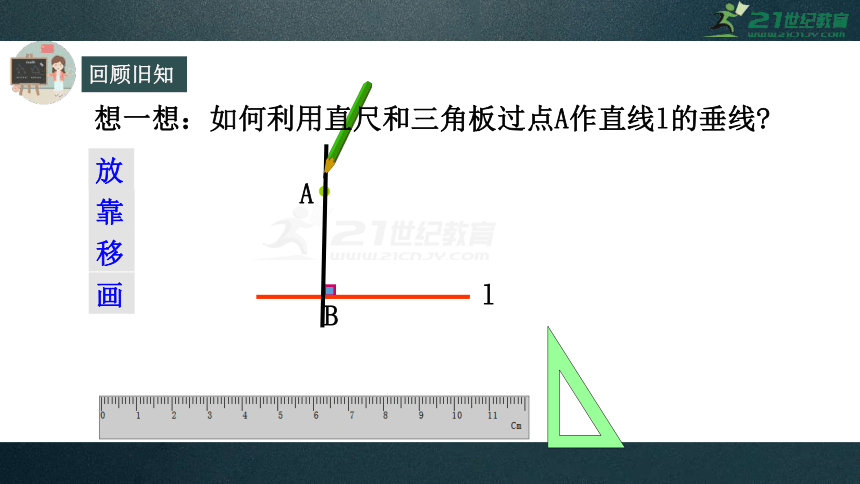
想一想:如何利用直尺和三角板过点A作直线l的垂线?
画
放
移
靠
合作探究---三角形的高
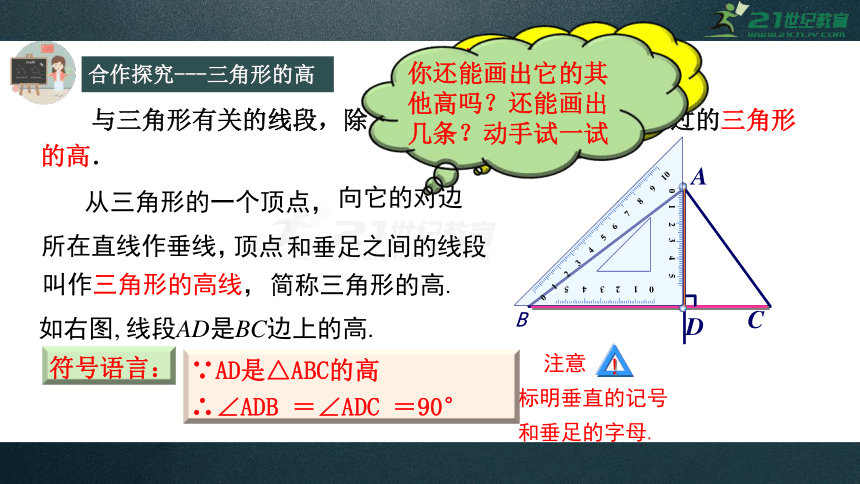
与三角形有关的线段,除了三条边,还有我们已经学过的三角形的高.
A
从三角形的一个顶点,
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫作三角形的高线,
简称三角形的高.
如右图,
线段AD是BC边上的高.
和垂足的字母.
注意
!
标明垂直的记号
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
你能过三角形顶点A,画出它的对边的高吗?
∵AD是△ABC的高
∴∠ADB
=∠ADC
=90°
符号语言:
你还能画出它的其他高吗?还能画出几条?动手试一试
合作探究---三角形的高
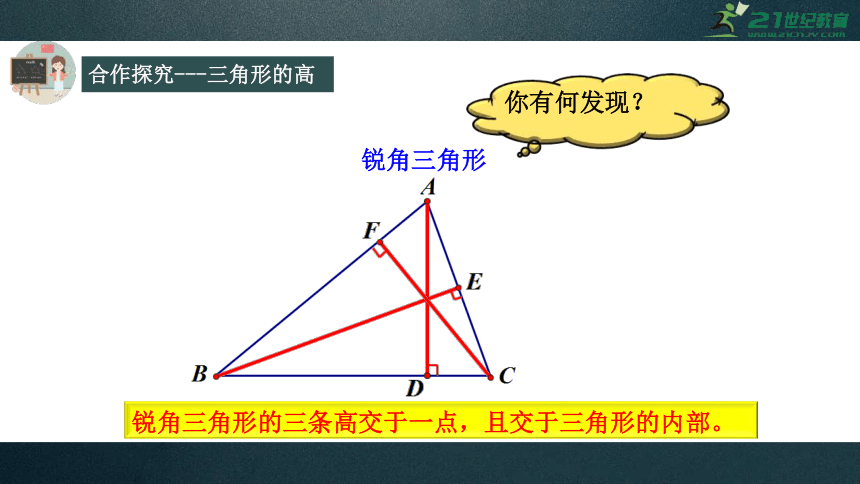
锐角三角形
锐角三角形的三条高交于一点,且交于三角形的内部。
你有何发现?
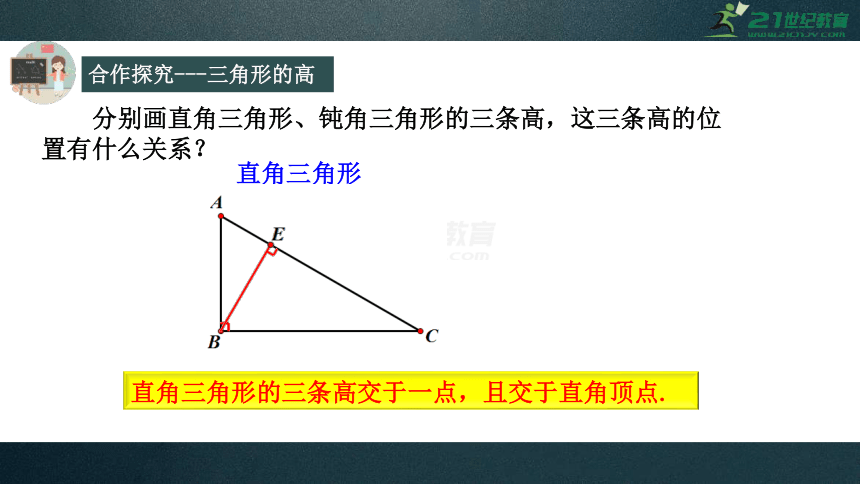
分别画直角三角形、钝角三角形的三条高,这三条高的位置有什么关系?
直角三角形
直角三角形的三条高交于一点,且交于直角顶点.
合作探究---三角形的高
合作探究---三角形的高
分别画直角三角形、钝角三角形的三条高,这三条高的位置有什么关系?
钝角三角形
钝角三角形的三条高没有交于一点.
钝角三角形的三条高所在直线交于
一点,且交于三角形的外部。
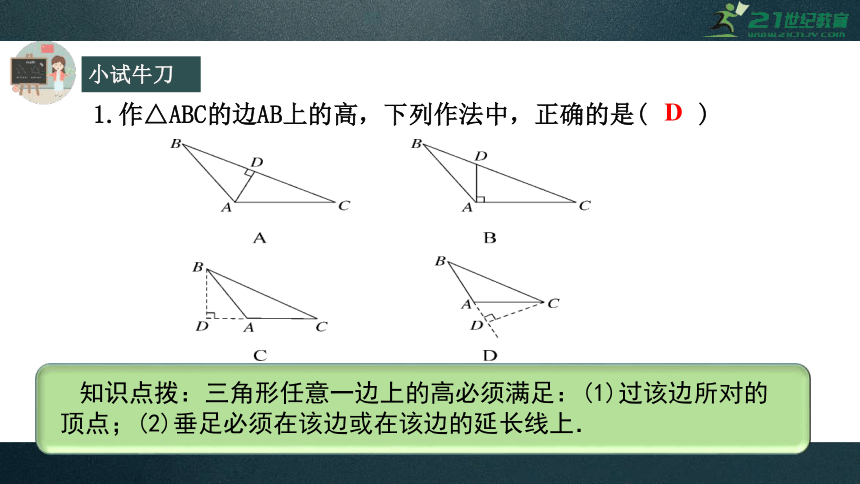
1.作△ABC的边AB上的高,下列作法中,正确的是( )
知识点拨:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
小试牛刀
小试牛刀
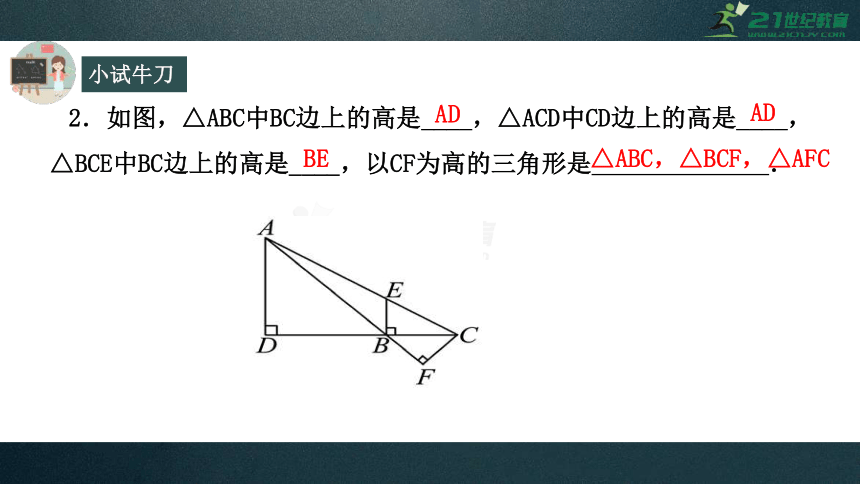
2.如图,△ABC中BC边上的高是____,△ACD中CD边上的高是____,△BCE中BC边上的高是____,以CF为高的三角形是
.
AD
AD
BE
△ABC,△BCF,△AFC
小试牛刀
如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
知识点拨:可利用面积相等作桥梁(但不求面积)求三角形的高,此解题方法通常称为“面积法”.
合作探究---三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线.
AE是BC边上的中线.
三角形的“中线”
B
A
C
A
BE=EC
E
∵AD是△ABC的中线
∴BD
=CD
=
BC
符号语言:
你能用同样方法,画出△ABC的另两条边上的中线吗?
合作探究---三角形的中线
你有何发现?
三角形的三条中线交于一点,且在三角形的内部.
合作探究---三角形的中线
钝角三角形和直角三角形的中线又是怎样的?折一折,画一画,并与同伴交流
三角形的三条中线交于一点,且都在三角形的内部.
三角形三条中线的交点,叫做三角形的重心.
小试牛刀
1、在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
知识点拨:一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差。
7cm
2.三角形一边上的中线把原三角形分成两个(
)
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
知识点拨:一边上的中线把原三角形分成两个面积相等的三角形。
合作探究---三角形的角平分线
三角形的角平分线的定义:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
注意:“三角形的角平分线”是一条线段.
∠1=∠2
∵BD是△ABC的角平分线
∴∠1=∠2=
符号语言:
合作探究---三角形的角平分线
思考:
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?
1、用量角器
2、将画出三角形并剪下,将它的一个角对折,使其两边重合.
A
B
C
A
D
合作探究---三角形的角平分线
分别画锐角三角形、直角三角形、钝角三角形的三条角平分线,这三条角平分线的位置有什么关系?
三角形的三条角平分线交于一点且均在三角形的内部.
小试牛刀
1.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是
( )
A.①②
B.③④
C.①④
D.②③
D
课后作业
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
2、如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
课堂小结
今天我们收获了哪些知识?
1.你能分别描述三角形中的几种重要线段及其特点吗?
2.你能说说什么是三角形的重心吗?
综合演练
1.下列说法正确的是
( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
知识点拨:所有三角形的三条角平分线、三条中线、三条高线(或其延长线)均交于一点,角平分线交点、中线交点都在三角形的内部;而对于高线的交点:锐角三角形在内部,直角三角形在直角顶点、钝角三角形在外部。其次角平分线、高线、中线均为线段。
综合演练
2.如图,AD⊥BC于点D,则图中以AD为高的
三角形有____个
6
3.如图,在△ABC中,CD是△ABC的角平分线,DE∥BC,交AC于点E,若∠ACB=60°,则∠EDC的度数是(
)
A.15°
B.30°
C.45°
D.60°
.
B
综合演练
4.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则AB=
2__,
BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,∠3=_________,
∠ACB=______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
综合演练
5.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,
求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C
)
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°=
9°.
B
A
C
D
E
综合演练
6.如图,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24和30两部分,求△ABC各边的长.
综合演练
7、
课后作业
课本教材第8页:3、4、8题
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
11.1.2
三角形的高、中线与角平分线
学习目标
1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
回顾旧知
l
A
B
想一想:如何利用直尺和三角板过点A作直线l的垂线?
画
放
移
靠
合作探究---三角形的高
与三角形有关的线段,除了三条边,还有我们已经学过的三角形的高.
A
从三角形的一个顶点,
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫作三角形的高线,
简称三角形的高.
如右图,
线段AD是BC边上的高.
和垂足的字母.
注意
!
标明垂直的记号
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
你能过三角形顶点A,画出它的对边的高吗?
∵AD是△ABC的高
∴∠ADB
=∠ADC
=90°
符号语言:
你还能画出它的其他高吗?还能画出几条?动手试一试
合作探究---三角形的高
锐角三角形
锐角三角形的三条高交于一点,且交于三角形的内部。
你有何发现?
分别画直角三角形、钝角三角形的三条高,这三条高的位置有什么关系?
直角三角形
直角三角形的三条高交于一点,且交于直角顶点.
合作探究---三角形的高
合作探究---三角形的高
分别画直角三角形、钝角三角形的三条高,这三条高的位置有什么关系?
钝角三角形
钝角三角形的三条高没有交于一点.
钝角三角形的三条高所在直线交于
一点,且交于三角形的外部。
1.作△ABC的边AB上的高,下列作法中,正确的是( )
知识点拨:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
小试牛刀
小试牛刀
2.如图,△ABC中BC边上的高是____,△ACD中CD边上的高是____,△BCE中BC边上的高是____,以CF为高的三角形是
.
AD
AD
BE
△ABC,△BCF,△AFC
小试牛刀
如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
知识点拨:可利用面积相等作桥梁(但不求面积)求三角形的高,此解题方法通常称为“面积法”.
合作探究---三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线.
AE是BC边上的中线.
三角形的“中线”
B
A
C
A
BE=EC
E
∵AD是△ABC的中线
∴BD
=CD
=
BC
符号语言:
你能用同样方法,画出△ABC的另两条边上的中线吗?
合作探究---三角形的中线
你有何发现?
三角形的三条中线交于一点,且在三角形的内部.
合作探究---三角形的中线
钝角三角形和直角三角形的中线又是怎样的?折一折,画一画,并与同伴交流
三角形的三条中线交于一点,且都在三角形的内部.
三角形三条中线的交点,叫做三角形的重心.
小试牛刀
1、在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
知识点拨:一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差。
7cm
2.三角形一边上的中线把原三角形分成两个(
)
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
知识点拨:一边上的中线把原三角形分成两个面积相等的三角形。
合作探究---三角形的角平分线
三角形的角平分线的定义:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
注意:“三角形的角平分线”是一条线段.
∠1=∠2
∵BD是△ABC的角平分线
∴∠1=∠2=
符号语言:
合作探究---三角形的角平分线
思考:
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?
1、用量角器
2、将画出三角形并剪下,将它的一个角对折,使其两边重合.
A
B
C
A
D
合作探究---三角形的角平分线
分别画锐角三角形、直角三角形、钝角三角形的三条角平分线,这三条角平分线的位置有什么关系?
三角形的三条角平分线交于一点且均在三角形的内部.
小试牛刀
1.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是
( )
A.①②
B.③④
C.①④
D.②③
D
课后作业
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
2、如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
课堂小结
今天我们收获了哪些知识?
1.你能分别描述三角形中的几种重要线段及其特点吗?
2.你能说说什么是三角形的重心吗?
综合演练
1.下列说法正确的是
( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
知识点拨:所有三角形的三条角平分线、三条中线、三条高线(或其延长线)均交于一点,角平分线交点、中线交点都在三角形的内部;而对于高线的交点:锐角三角形在内部,直角三角形在直角顶点、钝角三角形在外部。其次角平分线、高线、中线均为线段。
综合演练
2.如图,AD⊥BC于点D,则图中以AD为高的
三角形有____个
6
3.如图,在△ABC中,CD是△ABC的角平分线,DE∥BC,交AC于点E,若∠ACB=60°,则∠EDC的度数是(
)
A.15°
B.30°
C.45°
D.60°
.
B
综合演练
4.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则AB=
2__,
BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,∠3=_________,
∠ACB=______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
综合演练
5.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,
求∠DAE的大小.
解:
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-(∠ADC+∠C
)
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°=
9°.
B
A
C
D
E
综合演练
6.如图,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24和30两部分,求△ABC各边的长.
综合演练
7、
课后作业
课本教材第8页:3、4、8题
https://www.21cnjy.com/help/help_extract.php
