苏科版九下数学 5.4二次函数与一元二次方程教案
文档属性
| 名称 | 苏科版九下数学 5.4二次函数与一元二次方程教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 53.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-05 00:00:00 | ||
图片预览

文档简介
5.4
二次函数与一元二次方程(1)
班级:
姓名:
【学习目标】
1.体会函数与方程之间的联系,初步体会利用函数图像研究方程问题的方法;
2.理解二次函数图像与x轴(横轴)交点的个数与一元二次方程的根的个数之间的关系,理解方程有两个不等的实根、两个相等的实根和没有实根的函数图像特征;
3.理解一元二次方程的根就是二次函数与y=h(h是实数)图像交点的横坐标.
【学习重点】经历“类比——观察——发现——归纳”而得出二次函数与一元二次方程的关系的探索过程.
【学习难点】准确理解二次函数与一元二次方程的关系.
【学习过程】
1、
方法引领
想一想:一次函数y=x+1与一元一次方程x+1=0有怎样的关系?
二、自主构建
1.观察二次函数
的图像,你能确定一元二次方程
的根吗?
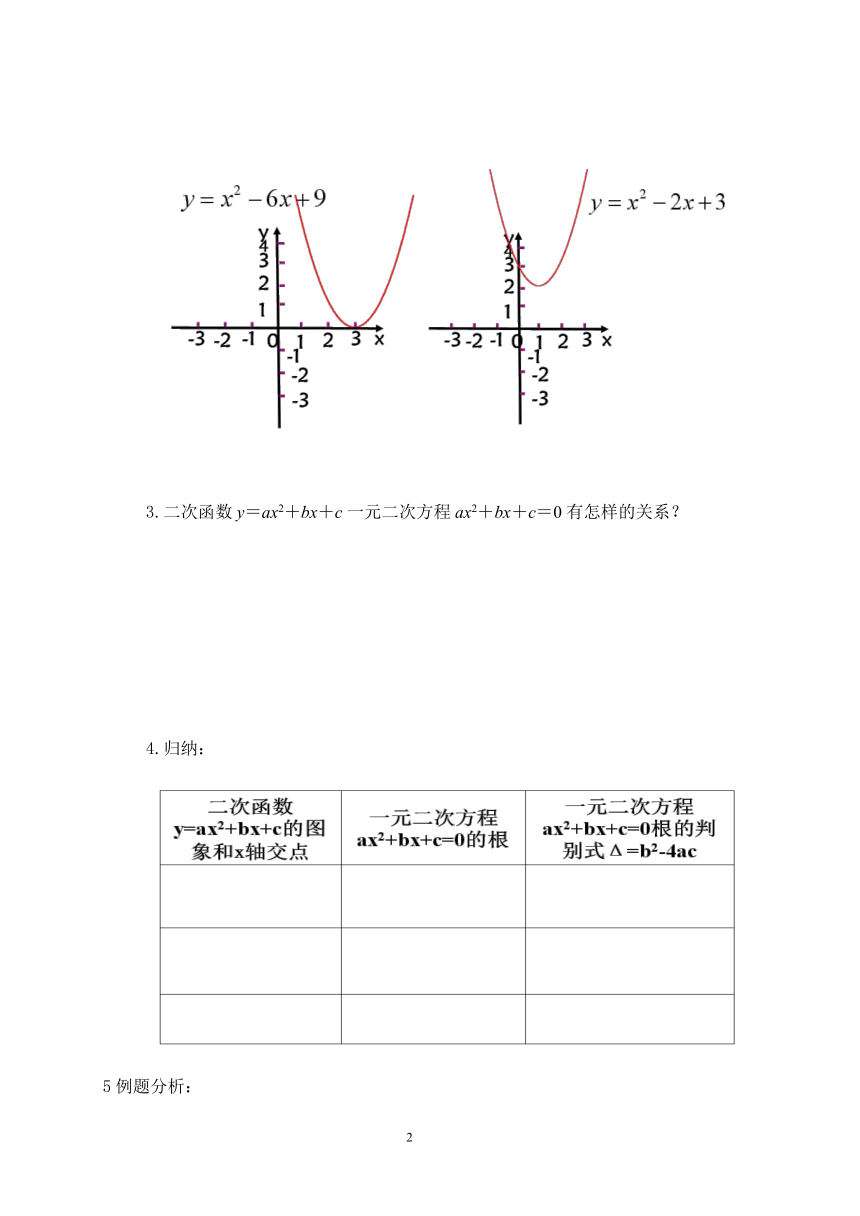
2.观察下列图像,分别说出一元二次方程x2-6x+9=0,x2-2x+3=0的根?
3.二次函数y=ax2+bx+c一元二次方程ax2+bx+c=0有怎样的关系?
4.归纳:
5例题分析:
例1.
不画图像,你能判断函数的图像y=x2+6x-6与x轴是否有公共点吗?请说明理由.
例2.已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.
三、互动体验
1.方程的根是
;则函数
的图像与x轴的交点有
个,其坐标是
.
2.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
.
3.若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴交点情况是(
)
A.无交点
B.只有一个交点
C.有两个交点
D.不能确定
4.抛物线y=ax2+bx+c(a≠0)的图象全部在x轴下方的条件是(
)
A.a<0
b2-4ac≤0.
B.a<0
b2-4ac>0
C.a>0
b2-4ac>0
D.a<0
b2-4ac<0
四、能力提升
阅读课本P“读一读”,试解决下面问题:
已知抛物线
y=x2-3x-4
(1)求抛物线与x轴交点坐标.
(2)当x为何值时y﹥0,y=0,y﹤0.
五、小结
1.一元二次方程的两个根即二次函数图像与x轴两个交点的横坐标,因此方程的根的情况决定着有无交点及交点的个数.
2.“给定函数值求自变量问题”转化为“解方程的问题”.
4
3
二次函数与一元二次方程(1)
班级:
姓名:
【学习目标】
1.体会函数与方程之间的联系,初步体会利用函数图像研究方程问题的方法;
2.理解二次函数图像与x轴(横轴)交点的个数与一元二次方程的根的个数之间的关系,理解方程有两个不等的实根、两个相等的实根和没有实根的函数图像特征;
3.理解一元二次方程的根就是二次函数与y=h(h是实数)图像交点的横坐标.
【学习重点】经历“类比——观察——发现——归纳”而得出二次函数与一元二次方程的关系的探索过程.
【学习难点】准确理解二次函数与一元二次方程的关系.
【学习过程】
1、
方法引领
想一想:一次函数y=x+1与一元一次方程x+1=0有怎样的关系?
二、自主构建
1.观察二次函数
的图像,你能确定一元二次方程
的根吗?
2.观察下列图像,分别说出一元二次方程x2-6x+9=0,x2-2x+3=0的根?
3.二次函数y=ax2+bx+c一元二次方程ax2+bx+c=0有怎样的关系?
4.归纳:
5例题分析:
例1.
不画图像,你能判断函数的图像y=x2+6x-6与x轴是否有公共点吗?请说明理由.
例2.已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.
三、互动体验
1.方程的根是
;则函数
的图像与x轴的交点有
个,其坐标是
.
2.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
.
3.若抛物线y=ax2+bx+c,当
a>0,c<0时,图象与x轴交点情况是(
)
A.无交点
B.只有一个交点
C.有两个交点
D.不能确定
4.抛物线y=ax2+bx+c(a≠0)的图象全部在x轴下方的条件是(
)
A.a<0
b2-4ac≤0.
B.a<0
b2-4ac>0
C.a>0
b2-4ac>0
D.a<0
b2-4ac<0
四、能力提升
阅读课本P“读一读”,试解决下面问题:
已知抛物线
y=x2-3x-4
(1)求抛物线与x轴交点坐标.
(2)当x为何值时y﹥0,y=0,y﹤0.
五、小结
1.一元二次方程的两个根即二次函数图像与x轴两个交点的横坐标,因此方程的根的情况决定着有无交点及交点的个数.
2.“给定函数值求自变量问题”转化为“解方程的问题”.
4
3
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
