1.1 生活中的立体图形同步练习题(含答案)
文档属性
| 名称 | 1.1 生活中的立体图形同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章
丰富的图形世界
1
生活中的立体图形
考点知识清单
考点1
常见几何体的分类
例1(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称。
(2)将这些几何体分类,并写出分类的理由。
思路提示:(1)根据正方体、长方体、圆柱、圆锥、球、棱柱等常见几何体的图形特征,一一进行识别;(2)常见几何体的分类,一般按柱体、锥体、球体,或组成面的平或曲进行划分。
方法归纳
1.首先根据立体图形的底面的个数确定它是柱体、锥体还是球体,然后根据其侧面是否为多边形来判断它是棱柱(锥),还是圆柱(锥)。
2.对几何体进行分类时,首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.注意柱体包括圆柱和棱柱,锥体包括圆锥和棱锥。
考题训练
1.下列标注的图形名称与图形不相符的是(
)
2.下列物体的形状属于球体的是(
)
3.下列图形中属于棱柱的有(
)
A.2个
B.3个
C.4个
D.5个
4.下列图形中,含有曲面的是(
)
A.①②
B.①③
C.②③
D.②④
5.如图所示为8个立体图形。
其中,是柱体的序号为_____________;是锥体的序号为___________;是球的序号为____________。
考点2
棱柱的概念及特征
例2
如图,一个正五棱柱的底面边长为2cm、高为4cm。
(1)这个棱柱共有多少个面?计算出它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数。
思路提示:可以先识别这个几何体是几棱柱,然后再根据棱柱的顶点数、面数、棱的条数的规律公式作答,也可根据图形直观地数一数获得结论,并通过棱柱的结构特征发现其具有的规律,或者通过数几种简单棱柱的各项数据去探索规律。
方法归纳
1.棱柱可以分为直棱柱和斜棱柱.在初中阶段研究的棱柱都是直棱柱。
2.在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱.相关特征:
(1)棱柱的所有侧棱长都相等;
(2)棱柱的上、下底面的形状相同,侧面的形状都是长方形;
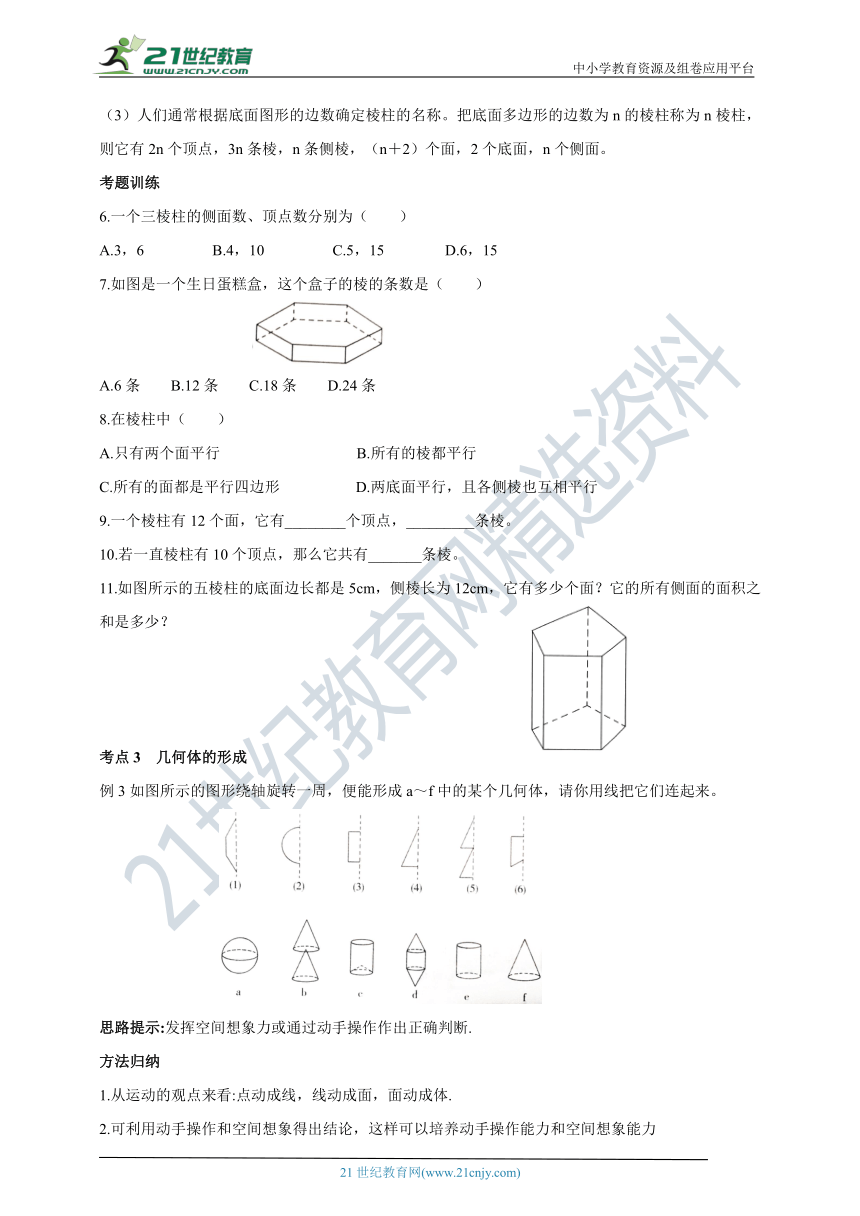
(3)人们通常根据底面图形的边数确定棱柱的名称。把底面多边形的边数为n的棱柱称为n棱柱,则它有2n个顶点,3n条棱,n条侧棱,(n+2)个面,2个底面,n个侧面。
考题训练
6.一个三棱柱的侧面数、顶点数分别为(
)
A.3,6
B.4,10
C.5,15
D.6,15
7.如图是一个生日蛋糕盒,这个盒子的棱的条数是(
)
A.6条
B.12条
C.18条
D.24条
8.在棱柱中(
)
A.只有两个面平行
B.所有的棱都平行
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也互相平行
9.一个棱柱有12个面,它有________个顶点,_________条棱。
10.若一直棱柱有10个顶点,那么它共有_______条棱。
11.如图所示的五棱柱的底面边长都是5cm,侧棱长为12cm,它有多少个面?它的所有侧面的面积之和是多少?
考点3
几何体的形成
例3如图所示的图形绕轴旋转一周,便能形成a~f中的某个几何体,请你用线把它们连起来。
思路提示:发挥空间想象力或通过动手操作作出正确判断.
方法归纳
1.从运动的观点来看:点动成线,线动成面,面动成体.
2.可利用动手操作和空间想象得出结论,这样可以培养动手操作能力和空间想象能力
考题训练
12.下列现象能说明“面动成体”的是(
)
A.天空划过一道流星
B.旋转一扇门,门在空中运动的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.汽车雨刷在挡风玻璃上刷出的痕迹
13.如图所示,把一个长方形绕着给定的直线旋转一周后,可能形成的几何体是(
)
14.将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是(
)
15.将直角边分别为3和4的直角三角形绕直角边旋转一周,所得的立体图形的体积最大是多少?
提分突破
A
基础巩固
1.下列图形不是立体图形的是(
)
A.球
B.圆柱
C.圆锥
D.圆
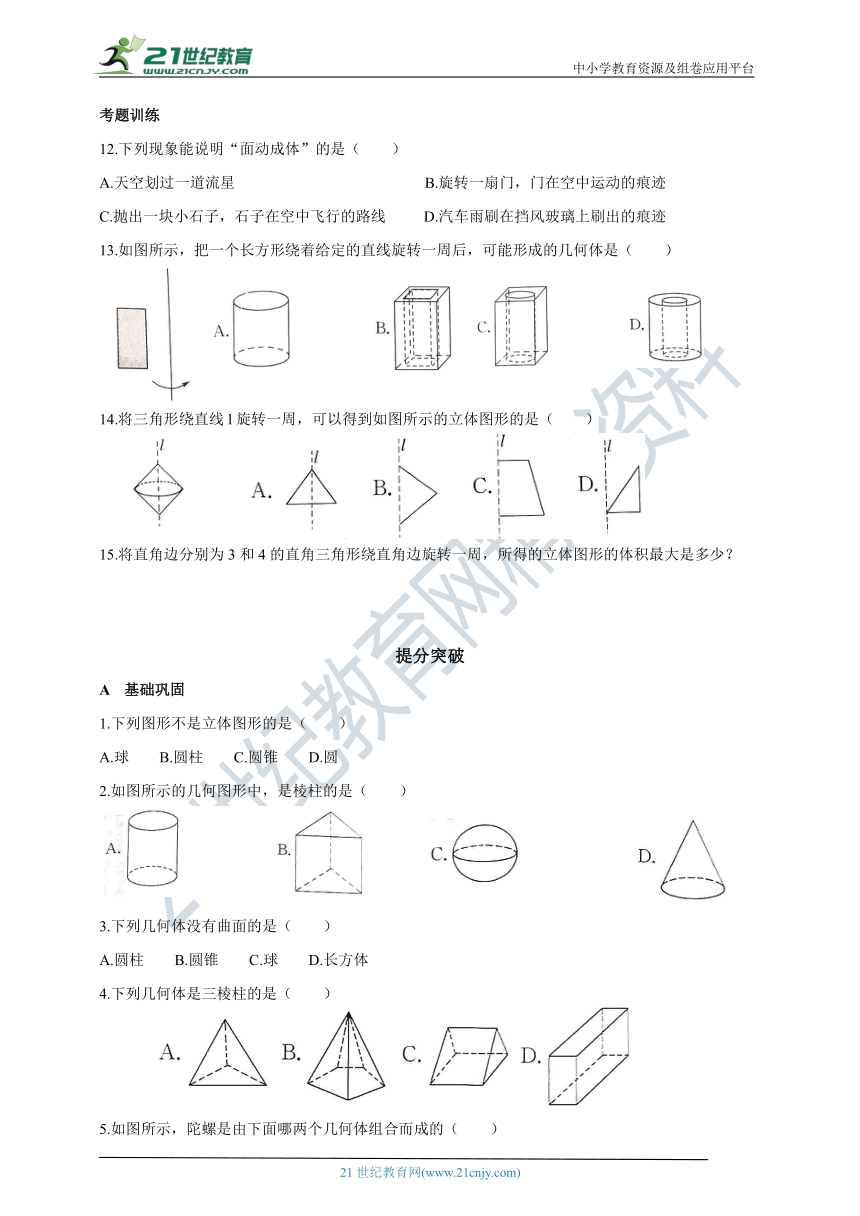
2.如图所示的几何图形中,是棱柱的是(
)
3.下列几何体没有曲面的是(
)
A.圆柱
B.圆锥
C.球
D.长方体
4.下列几何体是三棱柱的是(
)
5.如图所示,陀螺是由下面哪两个几何体组合而成的(
)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
6.如图,正方体的面有(
)
A.4个
B.5个
C.6个
D.7个
7.如图,图中的棱柱一共有(
)
A.6个面,12条棱
B.6个面,15条棱
C.7个面,12条棱
D.7个面,15条棱
8.下面现象说明“线动成面”的是(
)
A.把一枚硬币立在桌面上用力一转,形成一个球
B.写字时圆珠笔尖在纸上划过的痕迹
C.将一张纸对折后留下一道痕迹
D.一条拉直的细线切开了一块豆腐
9.将如图所示的几何图形,绕直线旋转一周得到的立体图形是(
)
B
综合运用
10.下列关于长方体的面的四个说法错误的是(
)
A.长方体的每个面都是长方形
B.长方体中每两个面都互相垂直
C.长方体中相对的两个面的面积相等
D.长方体中与一个面垂直的面有四个
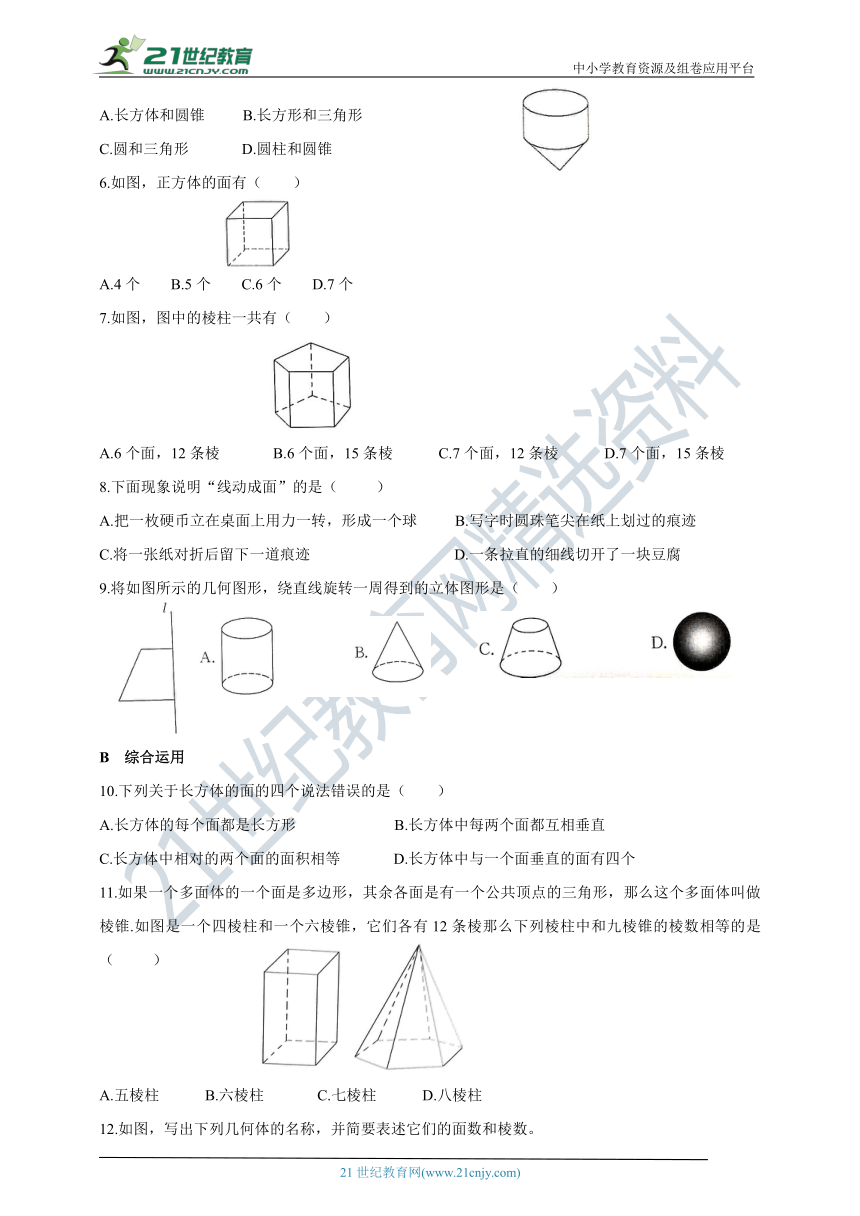
11.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱那么下列棱柱中和九棱锥的棱数相等的是(
)
A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
12.如图,写出下列几何体的名称,并简要表述它们的面数和棱数。
13.观察如图所示的直四棱柱。
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
C
拓展探究
14.观察是学习的一种重要能力。
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
15.台州奉化一果农有一批经过挑选的橙子要包装出售,现随意挑选10个橙子测量直径,数据分别为(单位:cm):7.9,7.8,8,7.9,8,8,7.9,7.9,7.8,7.8.橙子内包装模型的横截面如图①,凹型为半圆形,半圆的直径比这批橙子的大约平均值多0.2cm,现用纸箱作为外包装,内包装嵌入纸箱内,每箱装一层,一层装5×4个,如图②所示,且纸箱的高度比内包装高5cm.
(1)估计这批橙子的平均直径大约是多少;
(2)请根据题意设计出纸箱(不加盖子)的长、宽、高各为多少;(数据保留整数,设计时,长和宽比内包装各需加长0.5cm)
(3)加工成一只纸箱的外包装,需要硬纸板的面积为多少平方厘米?请给出一种较合理方案.(不计接头重叠部分,盖子顶面用透明纸)
参考答案
例1
解:(1)球、圆柱、圆锥、长方体、三棱柱;
(2)按柱体、锥体、球体分类,球属于球体,圆柱、长方体、三棱柱属于柱体,圆锥属于锥体;按组成面的平或曲分类,球、圆柱、圆锥属于一类,它们都含有曲面,长方体、三棱柱属于一类,它们的组成面都是平面。
考题训练
1.A
2.B
3.C
【解析】符合棱柱定义的有第一、二、六、七个几何体,共4个。
4.C
5.①②⑤⑦⑧
④⑥
③
例2
解:(1)这个棱柱共有7个面;侧面积为2×4×5=40(cm2);(2)这个棱柱共有10个顶点,15条棱;(3)n棱柱的顶点数为2n,面数为n+2,棱的条数为3n。
考题训练
6.A
7.C
8.D
9.
20
30
10.
15
11.解:这个五棱柱有7个面,沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是长方形,面积为5×12×5=300(cm2).答:这个五棱柱有7个面,所有侧面的面积之和是300
cm2.
例3
解:(1)—d;(2)—a;(3)—e;(4)—f;(5)—b;(6)—c。
考题训练
12.B
13.D
14.B
15.解:若以长3的直角边为圆锥的高,则V=π×42×3=16π;若以长4的直角边为圆锥的高,则V=π×32×4=12π.所以旋转成的圆锥的最大体积是16π.
【提分突破】
A
基础巩固
1.D
2.B
3.D
4.C
5.D
6.C
7.D
8.D
9.C
B
综合运用
10.B
【解析】A.长方体的每个面都是长方形,故本选项正确;B.长方体中相对的两个面互相平行,相邻的两个面互相垂直,故本选项错误;C.长方体中相对的两个面长与宽都相等,所以面积相等,故本选项正确;D.长方体中与一个面相邻的面有四个,所以与一个面垂直的面有四个,故本选项正确。
11.B
【解析】九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,A.五棱柱共15条棱,故A错误;B.六棱柱共18条棱,故B正确;C.七棱柱共21条棱,故C错误;D.八棱柱共24条棱,故D错误。
12.解:(1)该图形是圆锥,由1个曲面和1个平面构成;(2)该图形是六棱柱,由8个平面和18条棱构成;(3)该图形是长方体,由6个平面和12条棱构成;(4)该图形是圆柱,由1个曲面和2个平面构成;(5)该图形是球,由1个曲面构成。
13.解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;(2)侧面的个数与底面多边形的边数相等,都为4;(3)它的侧面积为20×8=160(cm2)
C
拓展探究
14.解:(1)在图①中,按上、下分类观察知,该几何体是八面体;(2)在图②中,按前、中、后分类观察知,该几何体是十二面体;(3)在图③中,按上、中、下分类观察知,该几何体是二十面体。
15.解:(1)(7.9+7.8+8+7.9+8+8+7.+7.9+7.8+7.8)÷10=7.9(cm);
(2)长=(7.9+0.2)×5+6+0.5=47(cm),宽=(7.9+0.2)×4+5+0.5≈38(cm),
高=(7.9+0.2)÷2+1+5≈10(cm);
(3)箱身=47×38+47×10×2+38×10×2=3486(cm2),
较合理的一种方案:面积为3486cm2。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第一章
丰富的图形世界
1
生活中的立体图形
考点知识清单
考点1
常见几何体的分类
例1(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称。
(2)将这些几何体分类,并写出分类的理由。
思路提示:(1)根据正方体、长方体、圆柱、圆锥、球、棱柱等常见几何体的图形特征,一一进行识别;(2)常见几何体的分类,一般按柱体、锥体、球体,或组成面的平或曲进行划分。
方法归纳
1.首先根据立体图形的底面的个数确定它是柱体、锥体还是球体,然后根据其侧面是否为多边形来判断它是棱柱(锥),还是圆柱(锥)。
2.对几何体进行分类时,首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.注意柱体包括圆柱和棱柱,锥体包括圆锥和棱锥。
考题训练
1.下列标注的图形名称与图形不相符的是(
)
2.下列物体的形状属于球体的是(
)
3.下列图形中属于棱柱的有(
)
A.2个
B.3个
C.4个
D.5个
4.下列图形中,含有曲面的是(
)
A.①②
B.①③
C.②③
D.②④
5.如图所示为8个立体图形。
其中,是柱体的序号为_____________;是锥体的序号为___________;是球的序号为____________。
考点2
棱柱的概念及特征
例2
如图,一个正五棱柱的底面边长为2cm、高为4cm。
(1)这个棱柱共有多少个面?计算出它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数。
思路提示:可以先识别这个几何体是几棱柱,然后再根据棱柱的顶点数、面数、棱的条数的规律公式作答,也可根据图形直观地数一数获得结论,并通过棱柱的结构特征发现其具有的规律,或者通过数几种简单棱柱的各项数据去探索规律。
方法归纳
1.棱柱可以分为直棱柱和斜棱柱.在初中阶段研究的棱柱都是直棱柱。
2.在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱.相关特征:
(1)棱柱的所有侧棱长都相等;
(2)棱柱的上、下底面的形状相同,侧面的形状都是长方形;
(3)人们通常根据底面图形的边数确定棱柱的名称。把底面多边形的边数为n的棱柱称为n棱柱,则它有2n个顶点,3n条棱,n条侧棱,(n+2)个面,2个底面,n个侧面。
考题训练
6.一个三棱柱的侧面数、顶点数分别为(
)
A.3,6
B.4,10
C.5,15
D.6,15
7.如图是一个生日蛋糕盒,这个盒子的棱的条数是(
)
A.6条
B.12条
C.18条
D.24条
8.在棱柱中(
)
A.只有两个面平行
B.所有的棱都平行
C.所有的面都是平行四边形
D.两底面平行,且各侧棱也互相平行
9.一个棱柱有12个面,它有________个顶点,_________条棱。
10.若一直棱柱有10个顶点,那么它共有_______条棱。
11.如图所示的五棱柱的底面边长都是5cm,侧棱长为12cm,它有多少个面?它的所有侧面的面积之和是多少?
考点3
几何体的形成
例3如图所示的图形绕轴旋转一周,便能形成a~f中的某个几何体,请你用线把它们连起来。
思路提示:发挥空间想象力或通过动手操作作出正确判断.
方法归纳
1.从运动的观点来看:点动成线,线动成面,面动成体.
2.可利用动手操作和空间想象得出结论,这样可以培养动手操作能力和空间想象能力
考题训练
12.下列现象能说明“面动成体”的是(
)
A.天空划过一道流星
B.旋转一扇门,门在空中运动的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.汽车雨刷在挡风玻璃上刷出的痕迹
13.如图所示,把一个长方形绕着给定的直线旋转一周后,可能形成的几何体是(
)
14.将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是(
)
15.将直角边分别为3和4的直角三角形绕直角边旋转一周,所得的立体图形的体积最大是多少?
提分突破
A
基础巩固
1.下列图形不是立体图形的是(
)
A.球
B.圆柱
C.圆锥
D.圆
2.如图所示的几何图形中,是棱柱的是(
)
3.下列几何体没有曲面的是(
)
A.圆柱
B.圆锥
C.球
D.长方体
4.下列几何体是三棱柱的是(
)
5.如图所示,陀螺是由下面哪两个几何体组合而成的(
)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
6.如图,正方体的面有(
)
A.4个
B.5个
C.6个
D.7个
7.如图,图中的棱柱一共有(
)
A.6个面,12条棱
B.6个面,15条棱
C.7个面,12条棱
D.7个面,15条棱
8.下面现象说明“线动成面”的是(
)
A.把一枚硬币立在桌面上用力一转,形成一个球
B.写字时圆珠笔尖在纸上划过的痕迹
C.将一张纸对折后留下一道痕迹
D.一条拉直的细线切开了一块豆腐
9.将如图所示的几何图形,绕直线旋转一周得到的立体图形是(
)
B
综合运用
10.下列关于长方体的面的四个说法错误的是(
)
A.长方体的每个面都是长方形
B.长方体中每两个面都互相垂直
C.长方体中相对的两个面的面积相等
D.长方体中与一个面垂直的面有四个
11.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱那么下列棱柱中和九棱锥的棱数相等的是(
)
A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
12.如图,写出下列几何体的名称,并简要表述它们的面数和棱数。
13.观察如图所示的直四棱柱。
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
C
拓展探究
14.观察是学习的一种重要能力。
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
15.台州奉化一果农有一批经过挑选的橙子要包装出售,现随意挑选10个橙子测量直径,数据分别为(单位:cm):7.9,7.8,8,7.9,8,8,7.9,7.9,7.8,7.8.橙子内包装模型的横截面如图①,凹型为半圆形,半圆的直径比这批橙子的大约平均值多0.2cm,现用纸箱作为外包装,内包装嵌入纸箱内,每箱装一层,一层装5×4个,如图②所示,且纸箱的高度比内包装高5cm.
(1)估计这批橙子的平均直径大约是多少;
(2)请根据题意设计出纸箱(不加盖子)的长、宽、高各为多少;(数据保留整数,设计时,长和宽比内包装各需加长0.5cm)
(3)加工成一只纸箱的外包装,需要硬纸板的面积为多少平方厘米?请给出一种较合理方案.(不计接头重叠部分,盖子顶面用透明纸)
参考答案
例1
解:(1)球、圆柱、圆锥、长方体、三棱柱;
(2)按柱体、锥体、球体分类,球属于球体,圆柱、长方体、三棱柱属于柱体,圆锥属于锥体;按组成面的平或曲分类,球、圆柱、圆锥属于一类,它们都含有曲面,长方体、三棱柱属于一类,它们的组成面都是平面。
考题训练
1.A
2.B
3.C
【解析】符合棱柱定义的有第一、二、六、七个几何体,共4个。
4.C
5.①②⑤⑦⑧
④⑥
③
例2
解:(1)这个棱柱共有7个面;侧面积为2×4×5=40(cm2);(2)这个棱柱共有10个顶点,15条棱;(3)n棱柱的顶点数为2n,面数为n+2,棱的条数为3n。
考题训练
6.A
7.C
8.D
9.
20
30
10.
15
11.解:这个五棱柱有7个面,沿一条侧棱将其侧面全部展开成一个平面图形,这个图形是长方形,面积为5×12×5=300(cm2).答:这个五棱柱有7个面,所有侧面的面积之和是300
cm2.
例3
解:(1)—d;(2)—a;(3)—e;(4)—f;(5)—b;(6)—c。
考题训练
12.B
13.D
14.B
15.解:若以长3的直角边为圆锥的高,则V=π×42×3=16π;若以长4的直角边为圆锥的高,则V=π×32×4=12π.所以旋转成的圆锥的最大体积是16π.
【提分突破】
A
基础巩固
1.D
2.B
3.D
4.C
5.D
6.C
7.D
8.D
9.C
B
综合运用
10.B
【解析】A.长方体的每个面都是长方形,故本选项正确;B.长方体中相对的两个面互相平行,相邻的两个面互相垂直,故本选项错误;C.长方体中相对的两个面长与宽都相等,所以面积相等,故本选项正确;D.长方体中与一个面相邻的面有四个,所以与一个面垂直的面有四个,故本选项正确。
11.B
【解析】九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,A.五棱柱共15条棱,故A错误;B.六棱柱共18条棱,故B正确;C.七棱柱共21条棱,故C错误;D.八棱柱共24条棱,故D错误。
12.解:(1)该图形是圆锥,由1个曲面和1个平面构成;(2)该图形是六棱柱,由8个平面和18条棱构成;(3)该图形是长方体,由6个平面和12条棱构成;(4)该图形是圆柱,由1个曲面和2个平面构成;(5)该图形是球,由1个曲面构成。
13.解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;(2)侧面的个数与底面多边形的边数相等,都为4;(3)它的侧面积为20×8=160(cm2)
C
拓展探究
14.解:(1)在图①中,按上、下分类观察知,该几何体是八面体;(2)在图②中,按前、中、后分类观察知,该几何体是十二面体;(3)在图③中,按上、中、下分类观察知,该几何体是二十面体。
15.解:(1)(7.9+7.8+8+7.9+8+8+7.+7.9+7.8+7.8)÷10=7.9(cm);
(2)长=(7.9+0.2)×5+6+0.5=47(cm),宽=(7.9+0.2)×4+5+0.5≈38(cm),
高=(7.9+0.2)÷2+1+5≈10(cm);
(3)箱身=47×38+47×10×2+38×10×2=3486(cm2),
较合理的一种方案:面积为3486cm2。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
