湘教版七年级下册数学 4.1.2 相交直线所成的角课件 (共21张PPT)
文档属性
| 名称 | 湘教版七年级下册数学 4.1.2 相交直线所成的角课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 17:32:50 | ||
图片预览



文档简介
(共21张PPT)
4.1
——4.1.2
相交直线所成的角
平面上两条直线的位置关系
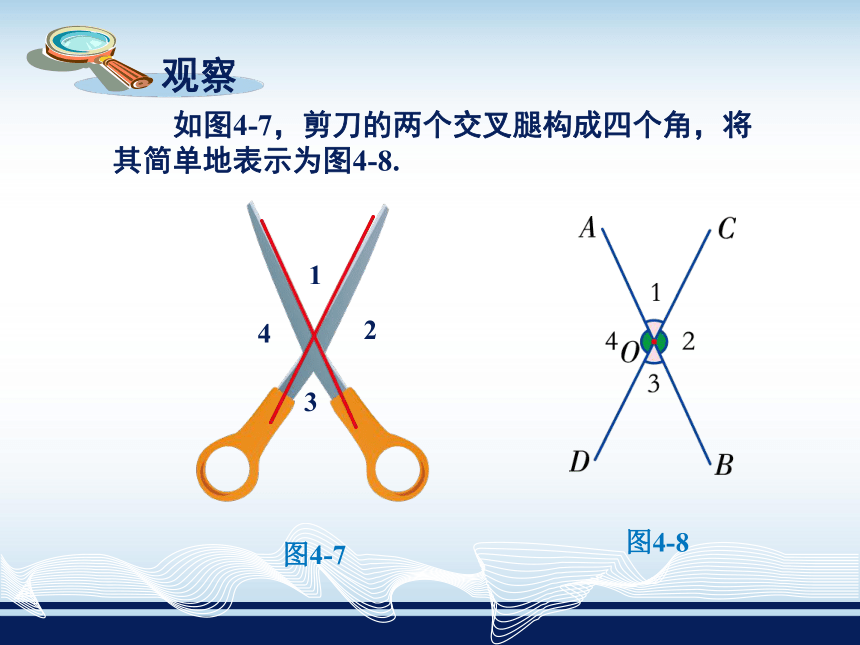
如图4-7,剪刀的两个交叉腿构成四个角,将其简单地表示为图4-8.
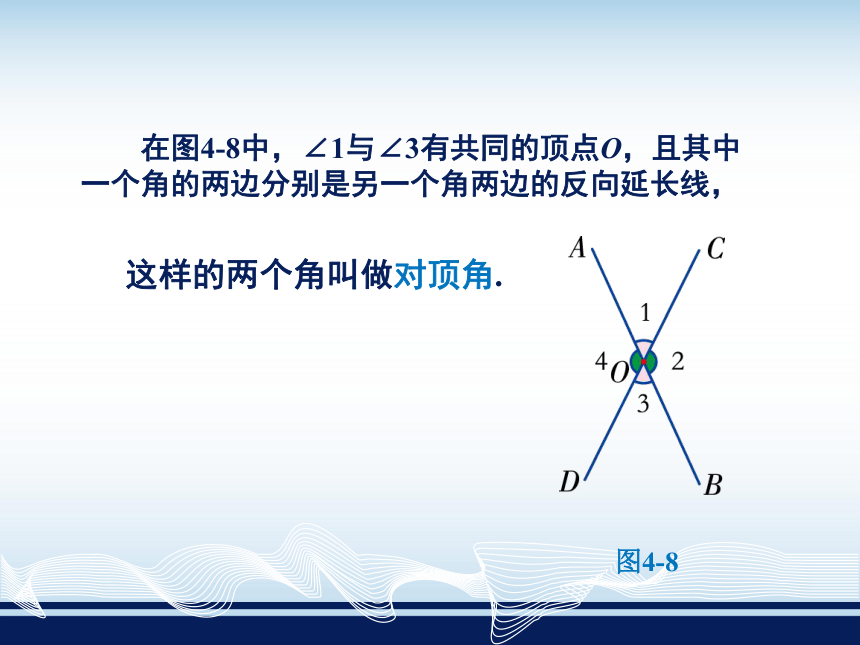
在图4-8中,∠1与∠3有共同的顶点O,且其中一个角的两边分别是另一个角两边的反向延长线,
这样的两个角叫做对顶角.
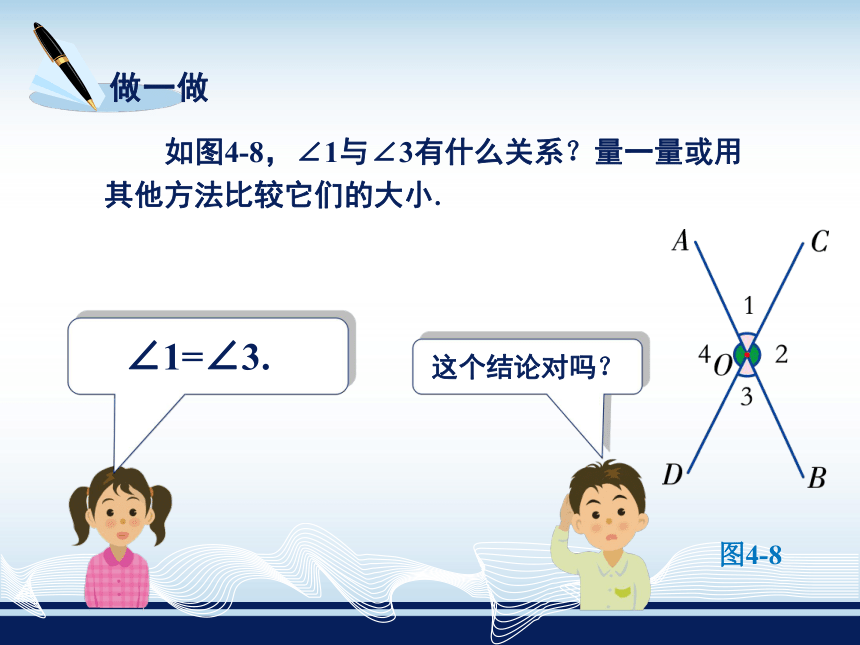
如图4-8,∠1与∠3有什么关系?量一量或用其他方法比较它们的大小.
∠1=∠3.
这个结论对吗?
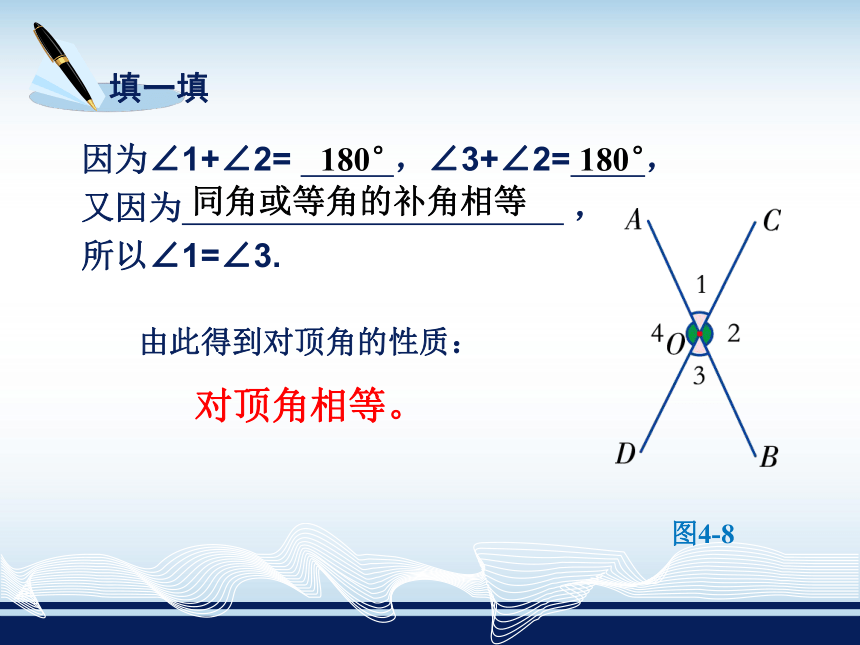
因为∠1+∠2=
,∠3+∠2=
,
又因为
,
所以∠1=∠3.
由此得到对顶角的性质:
对顶角相等。
180°
180°
同角或等角的补角相等
举例说说生活中对顶角的例子
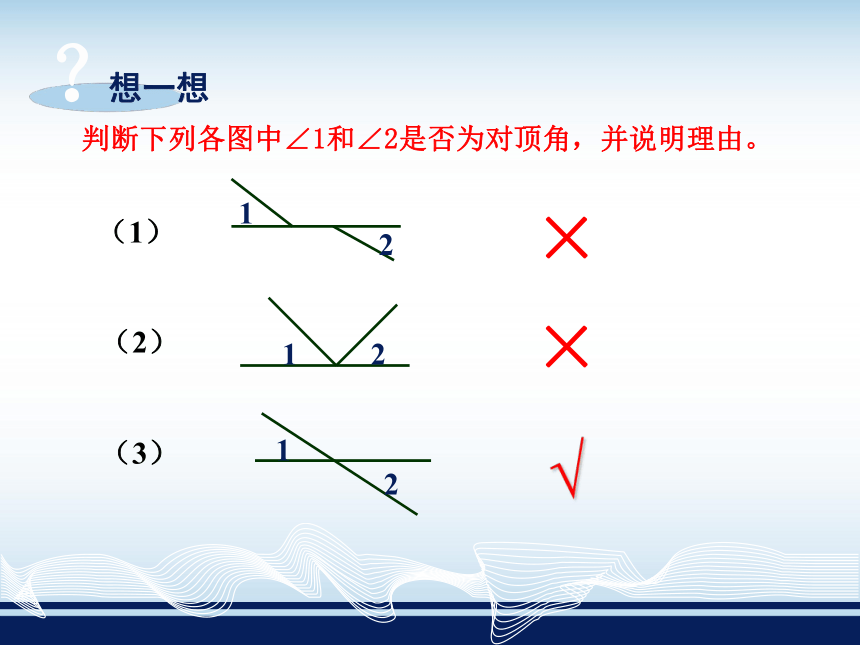
判断下列各图中∠1和∠2是否为对顶角,并说明理由。
1
2
1
2
1
2
(1)
(3)
?
√
×
×
(2)
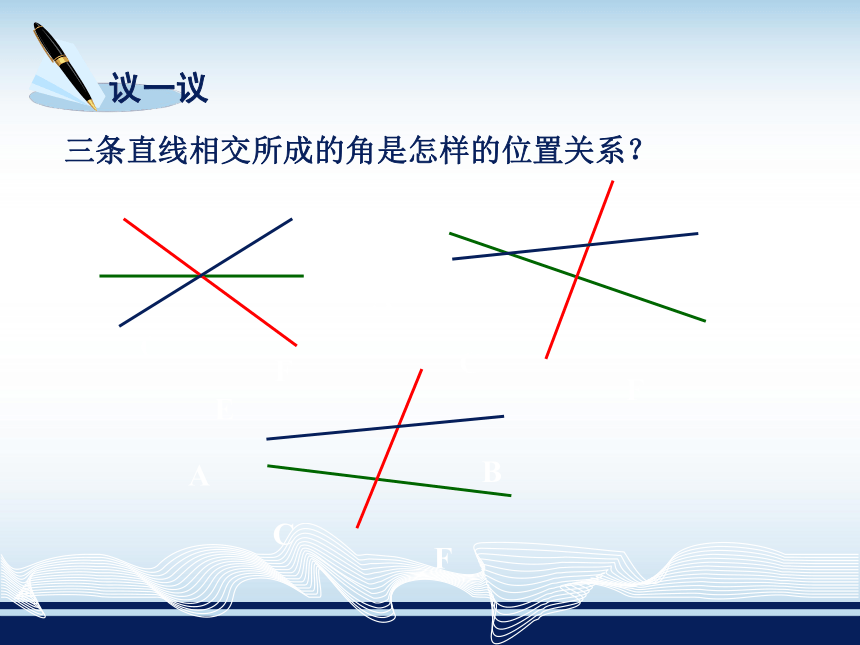
三条直线相交所成的角是怎样的位置关系?
设直线AB,CD都与第三条直线MN相交(有时也说直线AB和CD被第三条直线MN所截),可以构成8个角,如图所示.
直线MN----截线
直线AB、CD----被截直线
互动游戏(配对游戏):
老师说出一个角,同学们按要求再找出一个角与之配对。
(1)找出一个角,使它与老师说出的∠1,既在直线MN的同一侧,又在直线AB与直线CD的同一侧。
观察∠1和∠5两角:
1.∠1和∠5分别在直线AB,CD的同一方(上方);
2.并且它们都在直线MN的同侧(右侧)。
同位角
互动游戏(配对游戏):
(2)找出一个角,使它与老师说出的∠3,既在直线MN的两侧,又在直线AB与直线CD之间。
观察∠3和∠5两角:
1.∠3和∠5都在直线AB,CD之间;
2.并且它们分别在直线MN的两侧。
内错角
互动游戏(配对游戏):
(3)找出一个角,使它与老师说出的∠3,既在直线MN的同一侧,又在直线AB与直线CD之间。
观察∠3和∠6两角:
1.∠3和∠6都在直线AB,CD之间;
2.它们在直线MN的同一旁(左侧)。
同旁内角
如图:两只手的食指和拇指在同一平面内,它们构成的一对角可以看成是什么角?
例1
如图,直线EF与AB,CD相交,构成8个角.
指出
图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4,
∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,
∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2
如图,直线AB,CD被直线MN所截,同位角∠1
与∠2相等,那么内错角∠2与∠3相等吗?
解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3
(等量代换).
由上可知:两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
如图,直线a,b被直线c所截,找出图中所有的对顶角、同位角、内错角和同旁内角.
若∠1=∠5=108°,求其他角的度数.
解:对顶角有∠1与∠3,∠2与∠4;
同位角有∠1与∠5,∠2与∠6是;
内错角有∠3与∠5;
同旁内角有∠2与∠5.
∠3=∠1=108°,
∠4=
180°-∠1=180°-108°=72°;
∠2
=
∠4
=
72°;
∠6
=
180°-∠5=72°.
感谢聆听
敬请指导
4.1
——4.1.2
相交直线所成的角
平面上两条直线的位置关系
如图4-7,剪刀的两个交叉腿构成四个角,将其简单地表示为图4-8.
在图4-8中,∠1与∠3有共同的顶点O,且其中一个角的两边分别是另一个角两边的反向延长线,
这样的两个角叫做对顶角.
如图4-8,∠1与∠3有什么关系?量一量或用其他方法比较它们的大小.
∠1=∠3.
这个结论对吗?
因为∠1+∠2=
,∠3+∠2=
,
又因为
,
所以∠1=∠3.
由此得到对顶角的性质:
对顶角相等。
180°
180°
同角或等角的补角相等
举例说说生活中对顶角的例子
判断下列各图中∠1和∠2是否为对顶角,并说明理由。
1
2
1
2
1
2
(1)
(3)
?
√
×
×
(2)
三条直线相交所成的角是怎样的位置关系?
设直线AB,CD都与第三条直线MN相交(有时也说直线AB和CD被第三条直线MN所截),可以构成8个角,如图所示.
直线MN----截线
直线AB、CD----被截直线
互动游戏(配对游戏):
老师说出一个角,同学们按要求再找出一个角与之配对。
(1)找出一个角,使它与老师说出的∠1,既在直线MN的同一侧,又在直线AB与直线CD的同一侧。
观察∠1和∠5两角:
1.∠1和∠5分别在直线AB,CD的同一方(上方);
2.并且它们都在直线MN的同侧(右侧)。
同位角
互动游戏(配对游戏):
(2)找出一个角,使它与老师说出的∠3,既在直线MN的两侧,又在直线AB与直线CD之间。
观察∠3和∠5两角:
1.∠3和∠5都在直线AB,CD之间;
2.并且它们分别在直线MN的两侧。
内错角
互动游戏(配对游戏):
(3)找出一个角,使它与老师说出的∠3,既在直线MN的同一侧,又在直线AB与直线CD之间。
观察∠3和∠6两角:
1.∠3和∠6都在直线AB,CD之间;
2.它们在直线MN的同一旁(左侧)。
同旁内角
如图:两只手的食指和拇指在同一平面内,它们构成的一对角可以看成是什么角?
例1
如图,直线EF与AB,CD相交,构成8个角.
指出
图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4,
∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,
∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2
如图,直线AB,CD被直线MN所截,同位角∠1
与∠2相等,那么内错角∠2与∠3相等吗?
解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3
(等量代换).
由上可知:两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
如图,直线a,b被直线c所截,找出图中所有的对顶角、同位角、内错角和同旁内角.
若∠1=∠5=108°,求其他角的度数.
解:对顶角有∠1与∠3,∠2与∠4;
同位角有∠1与∠5,∠2与∠6是;
内错角有∠3与∠5;
同旁内角有∠2与∠5.
∠3=∠1=108°,
∠4=
180°-∠1=180°-108°=72°;
∠2
=
∠4
=
72°;
∠6
=
180°-∠5=72°.
感谢聆听
敬请指导
