2011年湖南省娄底市初中毕业学业联考试题卷
文档属性
| 名称 | 2011年湖南省娄底市初中毕业学业联考试题卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-29 16:50:01 | ||
图片预览



文档简介
2011年湖南省娄底市初中毕业学业联考试题卷(一)
亲爱的同学:欢迎参加数学考试!本学科试卷共设六道大题,满分120分,时量120分钟。
选择题:(每小题3分,共30分)
1.︱-32︱的值是 ( )
A.-3 B.3 C.9 D.-9
2.下列计算中,正确的是 ( )
A. x3+ x3 = x6 B. a6 ÷ a2 = a3 C.3a+5b=8ab D.(-ab)3=-a3b3
3.1nm为十亿分之一米,而个体中红细胞的直径约为0.0000077m,那么人体中红细胞直径的纳米数用科学记数表示为 ( )
A.7.7×103 nm B.7.7×102 nm C.7.7×104nm D.以上都不对
4.若关于方程(a-5)x2-4x-1=0有实数根,则a满足 ( )
A.a ≥1 B. a >1,且a≠5 C. a ≥1 ,且a≠5 D. a≠5
5.如右图所示,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若,∠A=30°,则∠1+∠2= ( )
A.50° B. 60° C. 45° D.以上都不对
6.某校九年(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是 ( )
A.从图中可以直接看出喜欢各种球类的具体人数。
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在喜欢各种球类的人数大小关系
7.如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为 ( )
A. B. C. D.
8. 在同一直角坐标系中,函数y=kx+k,与y=(k)的图像大致为( )
9.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A、C、E成一直线,那么E点离D点相距 ( )
A.500sin55°米 B. 500cos55°米 C. 500tan55°米 D.500cot 55°米
10.⊙O为△ABC的内切圆,如图,∠C=90°,AO的延长线交BC于D,AC=4,CD=1,则⊙O的半径为 ( )
A. B. C. D.
填空题:(每小题4分,共32分)
11. (-3)2-(兀-3.14)2=___________________。
12.函数的自变量的取值范围为___________________。
13.一元二次方程x2+2x-3=0的解为___________________。
14.若函数的图像经过点(2,-6),则函数的解析式可确定为=___________________。
15.在平行四边形、菱形、等腰梯形中,既是中心对称图形又是轴对称图形的有___________________。
16.如下图所示,△ABC中,D、E分别在AB、AC上,且DE与BC不平行,请加一个条件___________________,使△ADE∽△ACB。
17.已知点P到⊙O上的点的最短距离为3cm,最长距离为5cm,则⊙O的半径为___________________cm。
18.如图所示,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列说法:①PA=PB, ②∠1=∠2,③OP垂直平分AB,其中正确说法的序号是___________________。
三、解答题:(每小题7分,共21分)
19.当时,计算的值。
20.已知抛物线,(1)求它的顶点坐标;(2)求它与轴、轴的交点坐标。
21.某广告公司欲招聘策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项成绩如下表所示:
甲的成绩 乙的成绩 丙的成绩
创新能力 72 85 67
综合知识 50 74 70
计算机 88 45 67
若根据三次测试的平均成绩确定录取人选,那么谁被录取?说明理由。
若公司将创新能力、综合知识、计算机各项得分按4:3:1的比例确定各人的成绩,此时谁被录取?说明理由。
综合用一用,马到成功(满分8分)
22.一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为736,求原来的两位数。
耐心想一想,再接再厉(满分9分)
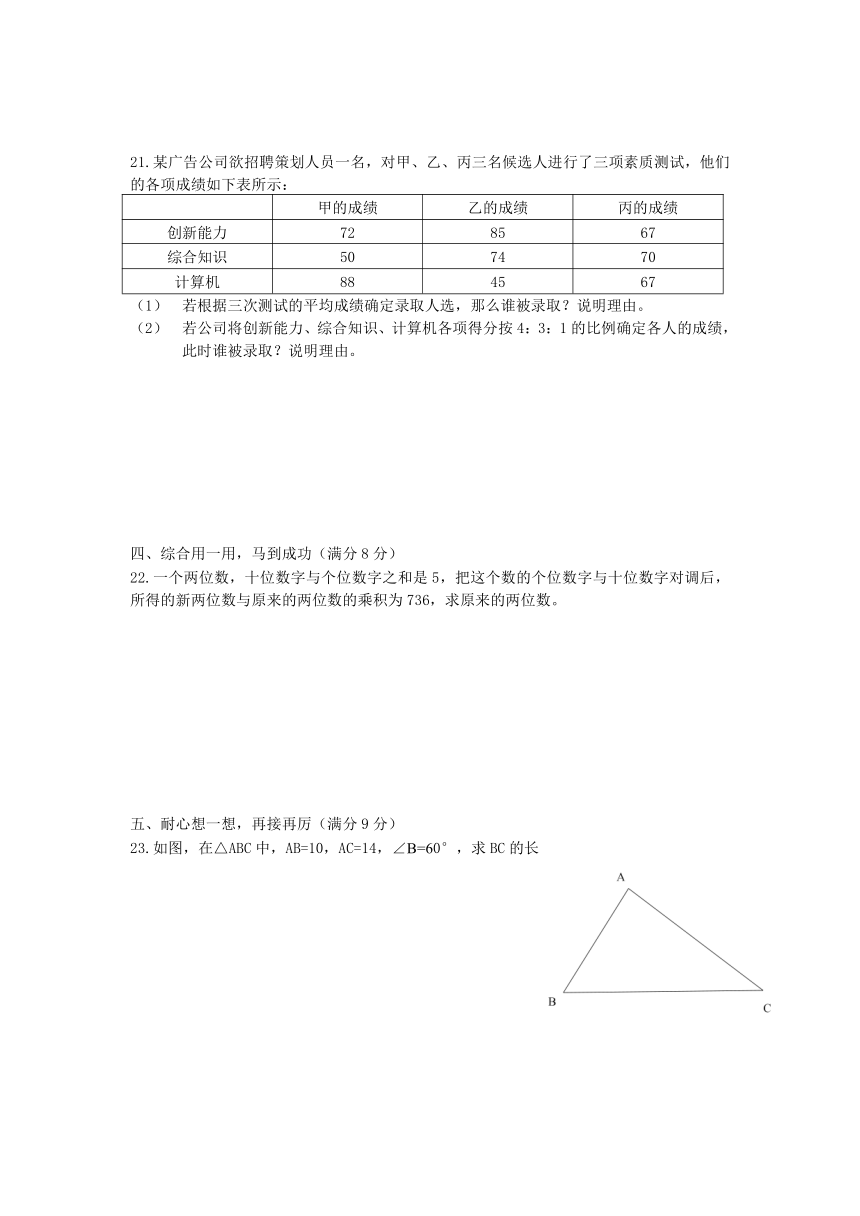
23.如图,在△ABC中,AB=10,AC=14,∠B=60°,求BC的长
探究试一试,超载自我(每题10分,满分20分)
24.已知抛物线与轴交于A(-1,0)和B(3,0)两点,且与轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)求抛物线的对称轴方程和顶点M的坐标;
(3)求四边形ABMC的面积。
25.如图,已知二次函数的图象与轴交于点A、B两点,与轴交于C点,⊙M是△ABC的外接圆。
(1)求阴影部分扇形AMC的面积;
(2)在轴的正半轴上有一点P,作PQ⊥轴交BC于Q,设PQ=K。
①设△OPQ的面积为S,求S关于K的函数关系式,并求出S的最大值;
②△CMQ能否与△AOC相似?若能,求出K的值;若不能,说明理由。
答案:
一、选择题
1. A 2. D 3.A 4.C 5. B
6. D 7. A 8. B 9. B 10. A
二、填空题
11. 8 12. x ≥-1 ,且x≠1, 13.
14. , 15. 菱 , 16. ∠AED=∠B,
17. 1
18.①、②、③
三、解答题
19.
20. 解:(1)∵
∴
=
∴顶点坐标(1,-5)
令,即
∴,
∴它与轴的交点坐标是(,0),(,0)
令x=0,则
∴它与轴的交点坐标是(0,-1)
21.解:
(1)=( 72+50+88)=70,
=(85+74+45)=68
=(67+70+67)=68
∵>,>
∴甲会被录取。
(2)=× 72+×50+×88=65.75,
=× 85+×74+×45=79,
=× 67+×70+×67=69.25,
∵>>
∴乙会被录取。
22.解:设原来的两位数十位上的数字为x,则个位上的数字为(5-x),依题意得:
(10x+5-x)〔10(5-x)+x〕=736
解这个方程得,
当时,5-x=3
当时,5-x=2
∴原来的两位数是23或32
答:原来的两位数是23或32
23. 解:如图过A点作AD垂直BC于D点.
在Rt△ABD中,AB=10,∠B=60°.
∵cosB=
∴cos60°=
∴BD=10 cos60°=5,AD
在Rt△ADC中,AC=14,
∴DC=
∴BC=BD+CD=16
24.解(1)设该抛物线的解析式为
∵它与轴交于点(0,3)
∴a·1·(-3)=3
∴a=-1
∴该抛物线的解析式为
(2) ∵
∴
∴抛物线的对称轴方程是,顶点M的坐标是(1,4)
(3)∵AO=1,OC=3,OE=1,ME=4,EB=OB-OE=2
∴S△AOC=,S梯△OCME =,
S△BEM=
∴四边形ABMC的面积=S△AOC+ S梯△OCME+ S△BEM=9
25.解:令
∴,
∴A点(-1,0),B点(3,0)
∴OB=3 ,OA=1
令x=0,则
∴C点(0,-3)
∴OC=3
∴OB=OC
∵∠BOC=90°,
∴∠OBC=45°
∴∠M=90°
在RtAOC中,AC=
在RtAMC中,,AM =BM
∴AM=
∴S扇形AMC=
(2)①∵PQ⊥AB ,∠PBQ=45°
∴∠PBQ =∠PQB =45°
∴PB=PQ=K
∴OP=OB-BP=3-k
∴s=·OP·PQ=k(3-k)=
∴s的最大值是
②当A、M、Q点在同一直线上时,
∠ACO =∠QCM ,∠AOC =∠QMC =90°
则△CMQ∽△AOC。
在Rt△BPQ中,根据勾股定理得BQ=
在Rt△OBC中,根据勾股定理得: BC=,
∴CQ=
∴
∴
∴
x
y
A
C
M
Q
P
O
B
y
x
M
B
E
C
A
O
x
y
A
C
M
Q
P
O
B
亲爱的同学:欢迎参加数学考试!本学科试卷共设六道大题,满分120分,时量120分钟。
选择题:(每小题3分,共30分)
1.︱-32︱的值是 ( )
A.-3 B.3 C.9 D.-9
2.下列计算中,正确的是 ( )
A. x3+ x3 = x6 B. a6 ÷ a2 = a3 C.3a+5b=8ab D.(-ab)3=-a3b3
3.1nm为十亿分之一米,而个体中红细胞的直径约为0.0000077m,那么人体中红细胞直径的纳米数用科学记数表示为 ( )
A.7.7×103 nm B.7.7×102 nm C.7.7×104nm D.以上都不对
4.若关于方程(a-5)x2-4x-1=0有实数根,则a满足 ( )
A.a ≥1 B. a >1,且a≠5 C. a ≥1 ,且a≠5 D. a≠5
5.如右图所示,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若,∠A=30°,则∠1+∠2= ( )
A.50° B. 60° C. 45° D.以上都不对
6.某校九年(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是 ( )
A.从图中可以直接看出喜欢各种球类的具体人数。
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在喜欢各种球类的人数大小关系
7.如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为 ( )
A. B. C. D.
8. 在同一直角坐标系中,函数y=kx+k,与y=(k)的图像大致为( )
9.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A、C、E成一直线,那么E点离D点相距 ( )
A.500sin55°米 B. 500cos55°米 C. 500tan55°米 D.500cot 55°米
10.⊙O为△ABC的内切圆,如图,∠C=90°,AO的延长线交BC于D,AC=4,CD=1,则⊙O的半径为 ( )
A. B. C. D.
填空题:(每小题4分,共32分)
11. (-3)2-(兀-3.14)2=___________________。
12.函数的自变量的取值范围为___________________。
13.一元二次方程x2+2x-3=0的解为___________________。
14.若函数的图像经过点(2,-6),则函数的解析式可确定为=___________________。
15.在平行四边形、菱形、等腰梯形中,既是中心对称图形又是轴对称图形的有___________________。
16.如下图所示,△ABC中,D、E分别在AB、AC上,且DE与BC不平行,请加一个条件___________________,使△ADE∽△ACB。
17.已知点P到⊙O上的点的最短距离为3cm,最长距离为5cm,则⊙O的半径为___________________cm。
18.如图所示,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列说法:①PA=PB, ②∠1=∠2,③OP垂直平分AB,其中正确说法的序号是___________________。
三、解答题:(每小题7分,共21分)
19.当时,计算的值。
20.已知抛物线,(1)求它的顶点坐标;(2)求它与轴、轴的交点坐标。
21.某广告公司欲招聘策划人员一名,对甲、乙、丙三名候选人进行了三项素质测试,他们的各项成绩如下表所示:
甲的成绩 乙的成绩 丙的成绩
创新能力 72 85 67
综合知识 50 74 70
计算机 88 45 67
若根据三次测试的平均成绩确定录取人选,那么谁被录取?说明理由。
若公司将创新能力、综合知识、计算机各项得分按4:3:1的比例确定各人的成绩,此时谁被录取?说明理由。
综合用一用,马到成功(满分8分)
22.一个两位数,十位数字与个位数字之和是5,把这个数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为736,求原来的两位数。
耐心想一想,再接再厉(满分9分)
23.如图,在△ABC中,AB=10,AC=14,∠B=60°,求BC的长
探究试一试,超载自我(每题10分,满分20分)
24.已知抛物线与轴交于A(-1,0)和B(3,0)两点,且与轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)求抛物线的对称轴方程和顶点M的坐标;
(3)求四边形ABMC的面积。
25.如图,已知二次函数的图象与轴交于点A、B两点,与轴交于C点,⊙M是△ABC的外接圆。
(1)求阴影部分扇形AMC的面积;
(2)在轴的正半轴上有一点P,作PQ⊥轴交BC于Q,设PQ=K。
①设△OPQ的面积为S,求S关于K的函数关系式,并求出S的最大值;
②△CMQ能否与△AOC相似?若能,求出K的值;若不能,说明理由。
答案:
一、选择题
1. A 2. D 3.A 4.C 5. B
6. D 7. A 8. B 9. B 10. A
二、填空题
11. 8 12. x ≥-1 ,且x≠1, 13.
14. , 15. 菱 , 16. ∠AED=∠B,
17. 1
18.①、②、③
三、解答题
19.
20. 解:(1)∵
∴
=
∴顶点坐标(1,-5)
令,即
∴,
∴它与轴的交点坐标是(,0),(,0)
令x=0,则
∴它与轴的交点坐标是(0,-1)
21.解:
(1)=( 72+50+88)=70,
=(85+74+45)=68
=(67+70+67)=68
∵>,>
∴甲会被录取。
(2)=× 72+×50+×88=65.75,
=× 85+×74+×45=79,
=× 67+×70+×67=69.25,
∵>>
∴乙会被录取。
22.解:设原来的两位数十位上的数字为x,则个位上的数字为(5-x),依题意得:
(10x+5-x)〔10(5-x)+x〕=736
解这个方程得,
当时,5-x=3
当时,5-x=2
∴原来的两位数是23或32
答:原来的两位数是23或32
23. 解:如图过A点作AD垂直BC于D点.
在Rt△ABD中,AB=10,∠B=60°.
∵cosB=
∴cos60°=
∴BD=10 cos60°=5,AD
在Rt△ADC中,AC=14,
∴DC=
∴BC=BD+CD=16
24.解(1)设该抛物线的解析式为
∵它与轴交于点(0,3)
∴a·1·(-3)=3
∴a=-1
∴该抛物线的解析式为
(2) ∵
∴
∴抛物线的对称轴方程是,顶点M的坐标是(1,4)
(3)∵AO=1,OC=3,OE=1,ME=4,EB=OB-OE=2
∴S△AOC=,S梯△OCME =,
S△BEM=
∴四边形ABMC的面积=S△AOC+ S梯△OCME+ S△BEM=9
25.解:令
∴,
∴A点(-1,0),B点(3,0)
∴OB=3 ,OA=1
令x=0,则
∴C点(0,-3)
∴OC=3
∴OB=OC
∵∠BOC=90°,
∴∠OBC=45°
∴∠M=90°
在RtAOC中,AC=
在RtAMC中,,AM =BM
∴AM=
∴S扇形AMC=
(2)①∵PQ⊥AB ,∠PBQ=45°
∴∠PBQ =∠PQB =45°
∴PB=PQ=K
∴OP=OB-BP=3-k
∴s=·OP·PQ=k(3-k)=
∴s的最大值是
②当A、M、Q点在同一直线上时,
∠ACO =∠QCM ,∠AOC =∠QMC =90°
则△CMQ∽△AOC。
在Rt△BPQ中,根据勾股定理得BQ=
在Rt△OBC中,根据勾股定理得: BC=,
∴CQ=
∴
∴
∴
x
y
A
C
M
Q
P
O
B
y
x
M
B
E
C
A
O
x
y
A
C
M
Q
P
O
B
同课章节目录
