小学数学西师大版六年级上2.5圆整理与复习 课件(共23张PPT)
文档属性
| 名称 | 小学数学西师大版六年级上2.5圆整理与复习 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-05 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
教学目标
1、引导学生回忆整理圆的认识,圆的周长和面积的意义及其计算公式的推导过程,并能熟练地应用公式进行计算;学会对所学知识进行整理的方法。
2、通过知识在生活中的运用,体验数学与生活的密切联系,培养学生数学源于生活又运用于生活的数学意识。
3、采取小组学习的方法,让学生在讨论、交流中参与学习活动,培养学生的合作意识和学习能力。
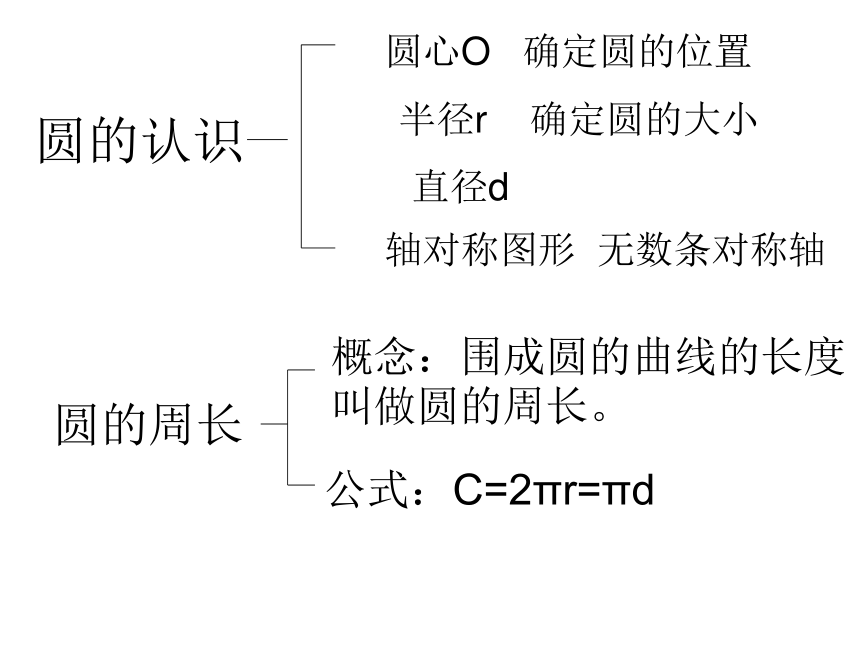
圆的认识
公式:C=2πr=πd
圆心O
确定圆的位置
半径r
确定圆的大小
直径d
轴对称图形
无数条对称轴
圆的周长
概念:围成圆的曲线的长度叫做圆的周长。
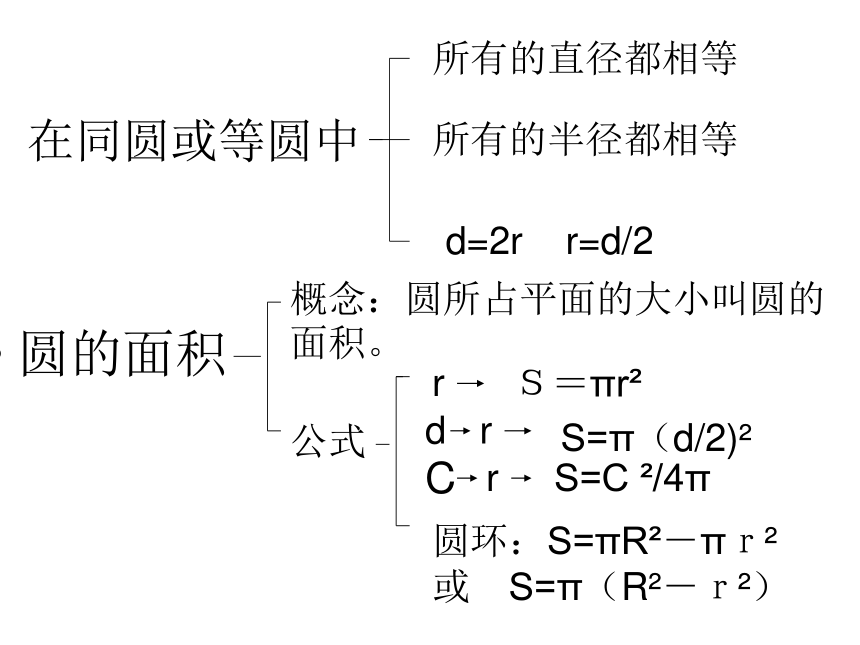
在同圆或等圆中
圆的面积
所有的直径都相等
所有的半径都相等
d=2r
r=d/2
概念:圆所占平面的大小叫圆的面积。
公式
r
S=πr?
d
r
S=π(d/2)?
C
r
S=C
?/4π
圆环:S=πR?-πr? 或 S=π(R?-r?)
独立思考
选择哪种整理形式?
怎样规划复习提纲?
三大板块的内容怎样安排?
记录时要注意什么?
合作整理
交流评价
认识圆形
1、圆的定义:圆是由封闭的曲线围成的一种平面图形。
圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。一般用字母O表示。它到圆上任意一点的距离都相等.
半径:连接圆心到圆上任意一点的线段叫做半径。一般用字母r表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
直径:通过圆心并且两端都在圆上的线段叫做直径。一般用字母d表示。直径是一个圆内最长的线段。
圆心确定圆的位置,半径确定圆的大小。
在同圆或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
长方形、正方形、等腰三角形、等腰梯形和圆都是轴对称图形。
只有1一条对称轴的图形有:
角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:
长方形
只有3条对称轴的图形是:
等边三角形
只有4条对称轴的图形是:
正方形
有无数条对称轴的图形是:
圆、圆环。
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π表示。
π≈3.14
围成圆的曲线的长度叫做圆的周长。用字母C表示
圆的
是
的
π倍。
C
d
固定值
在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
区分周长的一半和半圆的周长:
周长的一半:等于圆的周长÷2
计算方法:2π
r
÷
2
即
π
r
半圆的周长:等于圆的周长的一半加直径。
计算方法:πr+2r
即
5.14
r
圆所占平面的大小叫做圆的面积。
用字母S表示。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。顶点在圆心的角叫做圆心角。
将圆分成若干等分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
r
将圆分成若干等分
分的份数越多,拼成的图形越接近长方形。
r
r
因为:
长方形面积
=
长
×
宽
所以:
圆
的
面
积
=
πr
×
r
=
πr
2
S
=
πr
2
圆的面积计算公式:
圆环的面积
一个环形,外圆的半径是R,内圆的半径是r。(R=r+圆环的宽度.)
一个圆,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。而面积扩大或缩小的倍数是这倍数的平方倍。
两个圆:
半径比
=
直径比
=
周长比;而面积比等于这比的平方。
在同一个圆里,半径扩大3倍,那么直径和周长就都扩大3倍,而面积扩大9倍。
两个圆的半径比是2∶3,那么这两个圆的直径比和周长比都是2∶3,而面积比是4∶9
当长方形,正方形,圆的周长相等时,圆面积最大,正方形居中,长方形面积最小。反之,面积相同时,长方形的周长最长,正方形居中,圆周长最短。
当一个圆的半径增加a厘米时,它的周长就增加2πa厘米;当一个圆的直径增加a厘米时,它的周长就增加πa厘米。
常用各π值结果:
π
=
3.14
2π
=
6.28
3π
=
9.42
4π
=
12.56
5π
=
15.7
6π
=
18.84
7π
=
21.98
8π
=
25.12
9π
=
28.26
16π
=
50.24
25π
=
78.5
36π
=
113.04
64π
=
200.96
96π
=
301.44
(1)周长:20×2
+20×3.14
=40
+62.8
=102.8(cm)
面积:20×20=400(平方厘米)
(2)周长:3.14×4=12.56(厘米)
2
(3)周长:
2×2+
3.14×2=10.28(厘米)
拓展延伸
老师给你一条15.7厘米长的绳子,你能想办法或借助其它什么东西,围出一个最大的图形来吗?
总结
通过这节课的复习你有什么收获?还有什么困惑吗?
教学目标
1、引导学生回忆整理圆的认识,圆的周长和面积的意义及其计算公式的推导过程,并能熟练地应用公式进行计算;学会对所学知识进行整理的方法。
2、通过知识在生活中的运用,体验数学与生活的密切联系,培养学生数学源于生活又运用于生活的数学意识。
3、采取小组学习的方法,让学生在讨论、交流中参与学习活动,培养学生的合作意识和学习能力。
圆的认识
公式:C=2πr=πd
圆心O
确定圆的位置
半径r
确定圆的大小
直径d
轴对称图形
无数条对称轴
圆的周长
概念:围成圆的曲线的长度叫做圆的周长。
在同圆或等圆中
圆的面积
所有的直径都相等
所有的半径都相等
d=2r
r=d/2
概念:圆所占平面的大小叫圆的面积。
公式
r
S=πr?
d
r
S=π(d/2)?
C
r
S=C
?/4π
圆环:S=πR?-πr? 或 S=π(R?-r?)
独立思考
选择哪种整理形式?
怎样规划复习提纲?
三大板块的内容怎样安排?
记录时要注意什么?
合作整理
交流评价
认识圆形
1、圆的定义:圆是由封闭的曲线围成的一种平面图形。
圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。一般用字母O表示。它到圆上任意一点的距离都相等.
半径:连接圆心到圆上任意一点的线段叫做半径。一般用字母r表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
直径:通过圆心并且两端都在圆上的线段叫做直径。一般用字母d表示。直径是一个圆内最长的线段。
圆心确定圆的位置,半径确定圆的大小。
在同圆或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
长方形、正方形、等腰三角形、等腰梯形和圆都是轴对称图形。
只有1一条对称轴的图形有:
角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:
长方形
只有3条对称轴的图形是:
等边三角形
只有4条对称轴的图形是:
正方形
有无数条对称轴的图形是:
圆、圆环。
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π表示。
π≈3.14
围成圆的曲线的长度叫做圆的周长。用字母C表示
圆的
是
的
π倍。
C
d
固定值
在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
区分周长的一半和半圆的周长:
周长的一半:等于圆的周长÷2
计算方法:2π
r
÷
2
即
π
r
半圆的周长:等于圆的周长的一半加直径。
计算方法:πr+2r
即
5.14
r
圆所占平面的大小叫做圆的面积。
用字母S表示。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。顶点在圆心的角叫做圆心角。
将圆分成若干等分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
r
将圆分成若干等分
分的份数越多,拼成的图形越接近长方形。
r
r
因为:
长方形面积
=
长
×
宽
所以:
圆
的
面
积
=
πr
×
r
=
πr
2
S
=
πr
2
圆的面积计算公式:
圆环的面积
一个环形,外圆的半径是R,内圆的半径是r。(R=r+圆环的宽度.)
一个圆,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。而面积扩大或缩小的倍数是这倍数的平方倍。
两个圆:
半径比
=
直径比
=
周长比;而面积比等于这比的平方。
在同一个圆里,半径扩大3倍,那么直径和周长就都扩大3倍,而面积扩大9倍。
两个圆的半径比是2∶3,那么这两个圆的直径比和周长比都是2∶3,而面积比是4∶9
当长方形,正方形,圆的周长相等时,圆面积最大,正方形居中,长方形面积最小。反之,面积相同时,长方形的周长最长,正方形居中,圆周长最短。
当一个圆的半径增加a厘米时,它的周长就增加2πa厘米;当一个圆的直径增加a厘米时,它的周长就增加πa厘米。
常用各π值结果:
π
=
3.14
2π
=
6.28
3π
=
9.42
4π
=
12.56
5π
=
15.7
6π
=
18.84
7π
=
21.98
8π
=
25.12
9π
=
28.26
16π
=
50.24
25π
=
78.5
36π
=
113.04
64π
=
200.96
96π
=
301.44
(1)周长:20×2
+20×3.14
=40
+62.8
=102.8(cm)
面积:20×20=400(平方厘米)
(2)周长:3.14×4=12.56(厘米)
2
(3)周长:
2×2+
3.14×2=10.28(厘米)
拓展延伸
老师给你一条15.7厘米长的绳子,你能想办法或借助其它什么东西,围出一个最大的图形来吗?
总结
通过这节课的复习你有什么收获?还有什么困惑吗?
