11.2.1 三角形的内角(1)课件(共22张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角(1)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
人教版
八年级数学上
11.2.1
三角形的内角(1)
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.(重点)
情境导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
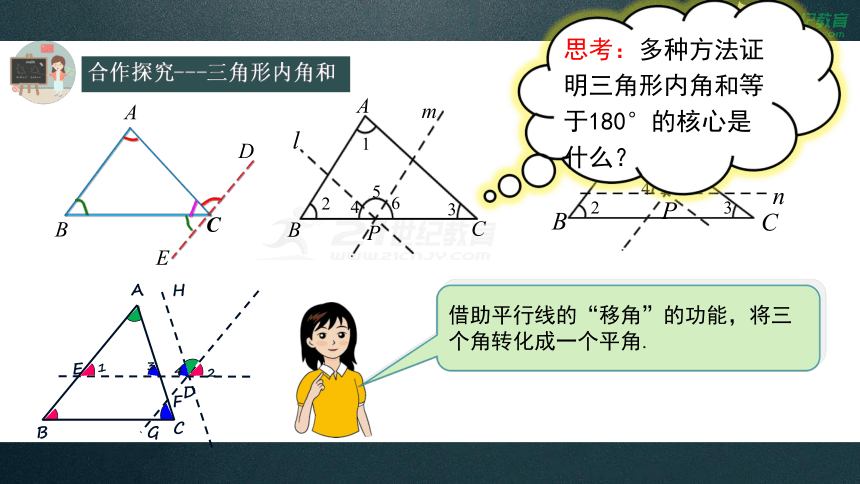
合作探究---三角形内角和
我们在小学已经知道,任意一个三角形的内角和等于180°。与三角形的形状、大小无关,所以它们的说法都是错误的。
当时我们是通过度量或剪拼的办法得出这一结论的,可是这种方法不能完全让人信服,所以我们需要寻求推理的方法去证明这一定理。
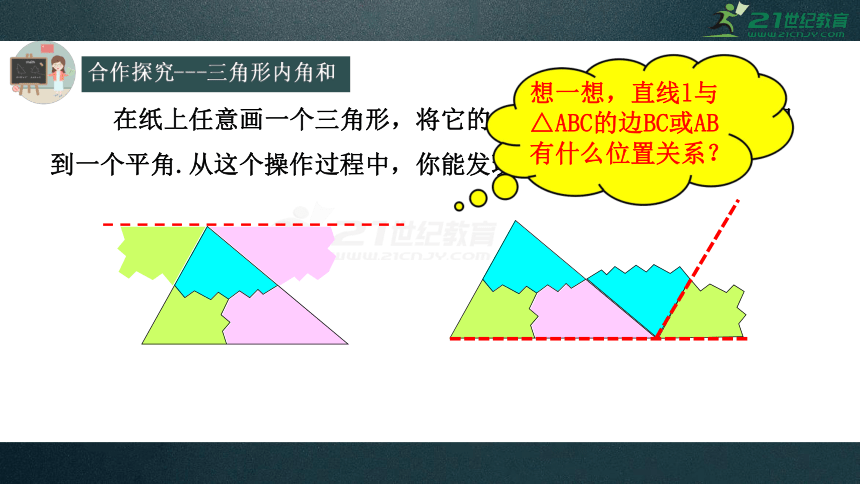
在纸上任意画一个三角形,将它的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
合作探究---三角形内角和
想一想,直线l与△ABC的边BC或AB有什么位置关系?
合作探究---三角形内角和
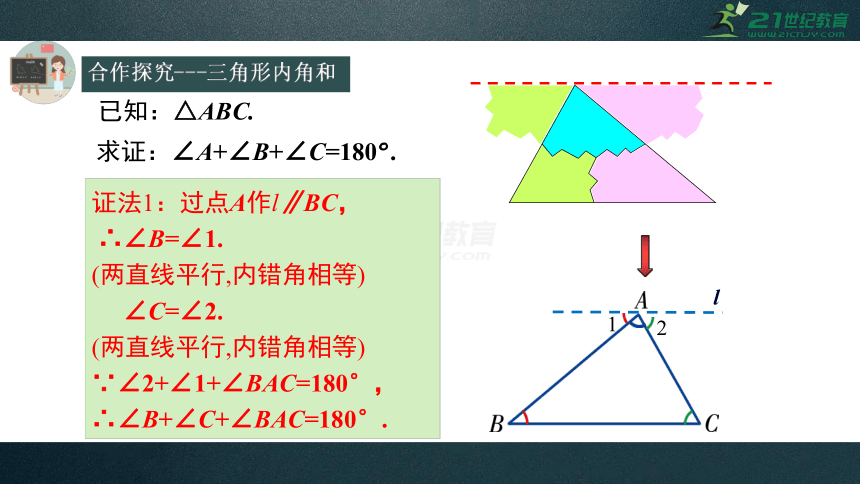
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
合作探究---三角形内角和
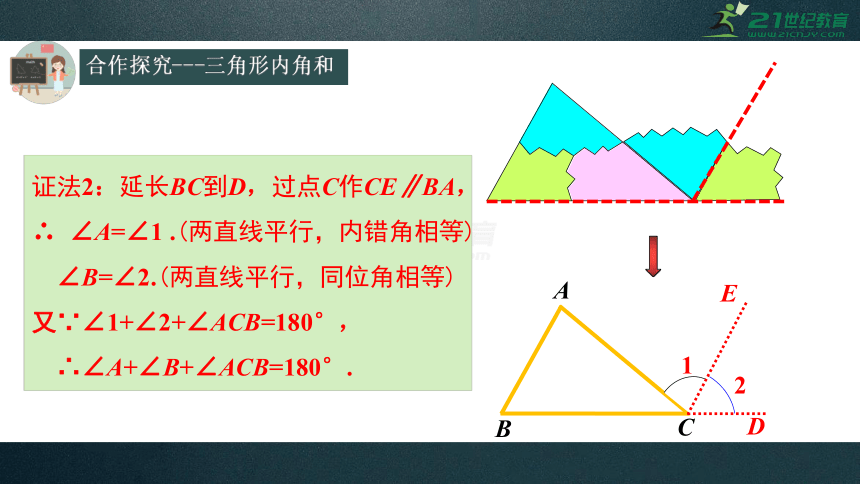
证法2:延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
合作探究---三角形内角和
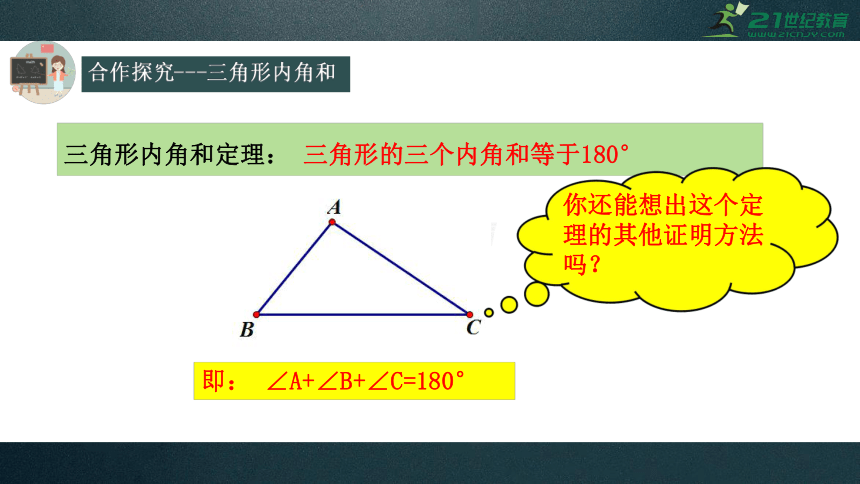
三角形内角和定理:
三角形的三个内角和等于180°
即:
∠A+∠B+∠C=180°
你还能想出这个定理的其他证明方法吗?
合作探究---三角形内角和
借助平行线的“移角”的功能,将三个角转化成一个平角.
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
C
A
B
1
2
3
4
5
l
P
6
m
n
B
G
C
2
4
A
3
E
D
F
H
1
思考:多种方法证明三角形内角和等于180°的核心是什么?
小试牛刀
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
2、在△ABC中,∠A
:∠B:∠C=1:2:3,则△ABC是
_________三角形
.
3、在△ABC中,
∠A=
∠B+10°,
∠C=
∠A
+
10°,
则
∠A=
,
∠
B=
,∠
C=
.
直角
60°
50°
70°
小试牛刀
4.如图,则∠1+∠2+∠3+∠4=___________
.
B
A
C
D
4
1
3
2
E
40°
(
280
°
能力提升
1.
如图,在△ABC
中,
∠BAC
=40°,
∠B
=75°,AD
是△ABC
的角平分线.求∠ADB
的度数.
C
B
D
A
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB=
∠BAC=20°,
在△ABD
中,∵∠B=75°,
∴∠ADB=180°-∠B-∠BAD
=180°-20°-75°=85°.
能力提升
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD=
∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
能力提升
2、在△ABC
中,
∠A
的度数是∠B
的度数的3倍,∠C
比∠B
大15°,求∠A,∠B,∠C的度数.
解:
设∠B为x,则∠A为3x,∠C为(x
+
15),
从而有
3x
+
x
+(x
+
15)=
180
°.
解得
x
=
33
°.
所以
3x
=
99
°
,
x
+
15
=
48
°.
答:
∠A,
∠B,
∠C的度数分别为99°,
33°,
48°.
能力提升
【变式题】在△ABC中,∠A=
∠B=
∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
知识点拨:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.
能力提升
解:∵∠A=
∠B=
∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,∴∠ACE=
×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
能力提升
3、如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
北
C
A
B
D
E
解:
∠CAB=
∠BAD-
∠CAD=80
°-50°=30°.
由AD//BE,得∠BAD+
∠ABE=180
°.
所以∠ABE=180
°-
∠BAD=180°-80°=100°,
∠ABC=
∠ABE-
∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180
°-
∠ABC-
∠
CAB
=180°-60°-30°
=90°,
答:从B岛看A,C两岛的视角∠ABC是60
°,从C岛看A,B两岛的视角
∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
能力提升
能力提升
【变式题】如图,B岛在A岛的南偏西54°方向上,C岛在A岛的南偏东51°方向上,B岛在C岛的北偏西81°方向上,求∠ABC的度数.
解:∠BAC=51°+54°=105°
∠ACB=81°-51°=30°
∴∠ABC=180°-105°-30°=45°
课堂小结
今天我们收获了哪些知识?
1.说一说三角形内角和定理?
2.怎样证明三角形内角和定理?
课后作业
课本教材第8页:1、3、7、9题
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
11.2.1
三角形的内角(1)
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内角和等于180°.(重点)
情境导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
合作探究---三角形内角和
我们在小学已经知道,任意一个三角形的内角和等于180°。与三角形的形状、大小无关,所以它们的说法都是错误的。
当时我们是通过度量或剪拼的办法得出这一结论的,可是这种方法不能完全让人信服,所以我们需要寻求推理的方法去证明这一定理。
在纸上任意画一个三角形,将它的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
合作探究---三角形内角和
想一想,直线l与△ABC的边BC或AB有什么位置关系?
合作探究---三角形内角和
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
合作探究---三角形内角和
证法2:延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
合作探究---三角形内角和
三角形内角和定理:
三角形的三个内角和等于180°
即:
∠A+∠B+∠C=180°
你还能想出这个定理的其他证明方法吗?
合作探究---三角形内角和
借助平行线的“移角”的功能,将三个角转化成一个平角.
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
C
A
B
1
2
3
4
5
l
P
6
m
n
B
G
C
2
4
A
3
E
D
F
H
1
思考:多种方法证明三角形内角和等于180°的核心是什么?
小试牛刀
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
2、在△ABC中,∠A
:∠B:∠C=1:2:3,则△ABC是
_________三角形
.
3、在△ABC中,
∠A=
∠B+10°,
∠C=
∠A
+
10°,
则
∠A=
,
∠
B=
,∠
C=
.
直角
60°
50°
70°
小试牛刀
4.如图,则∠1+∠2+∠3+∠4=___________
.
B
A
C
D
4
1
3
2
E
40°
(
280
°
能力提升
1.
如图,在△ABC
中,
∠BAC
=40°,
∠B
=75°,AD
是△ABC
的角平分线.求∠ADB
的度数.
C
B
D
A
解:∵AD平分∠CAB,∠BAC=40°,
∴∠DAB=
∠BAC=20°,
在△ABD
中,∵∠B=75°,
∴∠ADB=180°-∠B-∠BAD
=180°-20°-75°=85°.
能力提升
【变式题】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD=
∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
能力提升
2、在△ABC
中,
∠A
的度数是∠B
的度数的3倍,∠C
比∠B
大15°,求∠A,∠B,∠C的度数.
解:
设∠B为x,则∠A为3x,∠C为(x
+
15),
从而有
3x
+
x
+(x
+
15)=
180
°.
解得
x
=
33
°.
所以
3x
=
99
°
,
x
+
15
=
48
°.
答:
∠A,
∠B,
∠C的度数分别为99°,
33°,
48°.
能力提升
【变式题】在△ABC中,∠A=
∠B=
∠ACB,CD是△ABC的高,CE是∠ACB的平分线,求∠DCE的度数.
知识点拨:根据已知条件用∠A表示出∠B和∠ACB,利用三角形的内角和求出∠A,再求出∠ACB,∠ACD,最后根据角平分线的定义求出∠ACE即可求得∠DCE的度数.
能力提升
解:∵∠A=
∠B=
∠ACB,
设∠A=x,∴∠B=2x,∠ACB=3x.
∵∠A+∠B+∠ACB=180°,
∴x+2x+3x=180°,得x=30°,
∴∠A=30°,∠ACB=90°.
∵CD是△ABC的高,∴∠ADC=90°,
∴∠ACD=180°-90°-30°=60°.
∵CE是∠ACB的平分线,∴∠ACE=
×90°=45°,
∴∠DCE=∠ACD-∠ACE=60°-45°=15°.
能力提升
3、如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
北
C
A
B
D
E
解:
∠CAB=
∠BAD-
∠CAD=80
°-50°=30°.
由AD//BE,得∠BAD+
∠ABE=180
°.
所以∠ABE=180
°-
∠BAD=180°-80°=100°,
∠ABC=
∠ABE-
∠EBC=100°-40°=60°.
在△ABC中,
∠ACB=180
°-
∠ABC-
∠
CAB
=180°-60°-30°
=90°,
答:从B岛看A,C两岛的视角∠ABC是60
°,从C岛看A,B两岛的视角
∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
能力提升
能力提升
【变式题】如图,B岛在A岛的南偏西54°方向上,C岛在A岛的南偏东51°方向上,B岛在C岛的北偏西81°方向上,求∠ABC的度数.
解:∠BAC=51°+54°=105°
∠ACB=81°-51°=30°
∴∠ABC=180°-105°-30°=45°
课堂小结
今天我们收获了哪些知识?
1.说一说三角形内角和定理?
2.怎样证明三角形内角和定理?
课后作业
课本教材第8页:1、3、7、9题
https://www.21cnjy.com/help/help_extract.php
