2019-2020学年黑龙江省大庆市肇州县七年级下学期期末数学试卷(五四学制) (解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省大庆市肇州县七年级下学期期末数学试卷(五四学制) (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 363.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 06:42:58 | ||
图片预览




文档简介
2019-2020学年七年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.的平方根是( )
A.4
B.±4
C.±2
D.2
2.已知以下三个数,不能组成直角三角形的是( )
A.9、12、15
B.、3、2
C.0.3、0.4、0.5
D.32、42、52
3.如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(﹣2,0)
B.(0,﹣2)
C.(1,0)
D.(0,1)
4.已知a,b为两个连续的整数,且a<<b,则ba=( )
A.1
B.2
C.6
D.9
5.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.若函数y=(m+1)x|m|+2是一次函数,则m的值为( )
A.m=±1
B.m=﹣1
C.m=1
D.m≠﹣1
7.二元一次方程x+2y=9的所有正整数解有( )
A.1个
B.2个
C.3个
D.4个
8.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β﹣∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
9.某车间20名工人日加工零件数如表所示:这些工人日加工零件数的众数、中位数、平均数分别是( )
日加工零件数
4
5
6
7
8
人数
2
6
5
4
3
A.5、6、5
B.5、5、6
C.6、5、6
D.5、6、6
10.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
11.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是
12.计算:(﹣2)2019×(+2)2020=
.
13.已知直角三角形的两直角边长分别是3,4,则它的周长为
.
14.若关于x、y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为
.
15.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是
(填“甲”或“乙”).
16.已知关于x的一次函数y=mx+n的图象如图所示,则可化简为
.
17.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是
.
18.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
.
三、解答题.(共46分)
19.计算:÷﹣×+(﹣)﹣1.
20.解方程组.
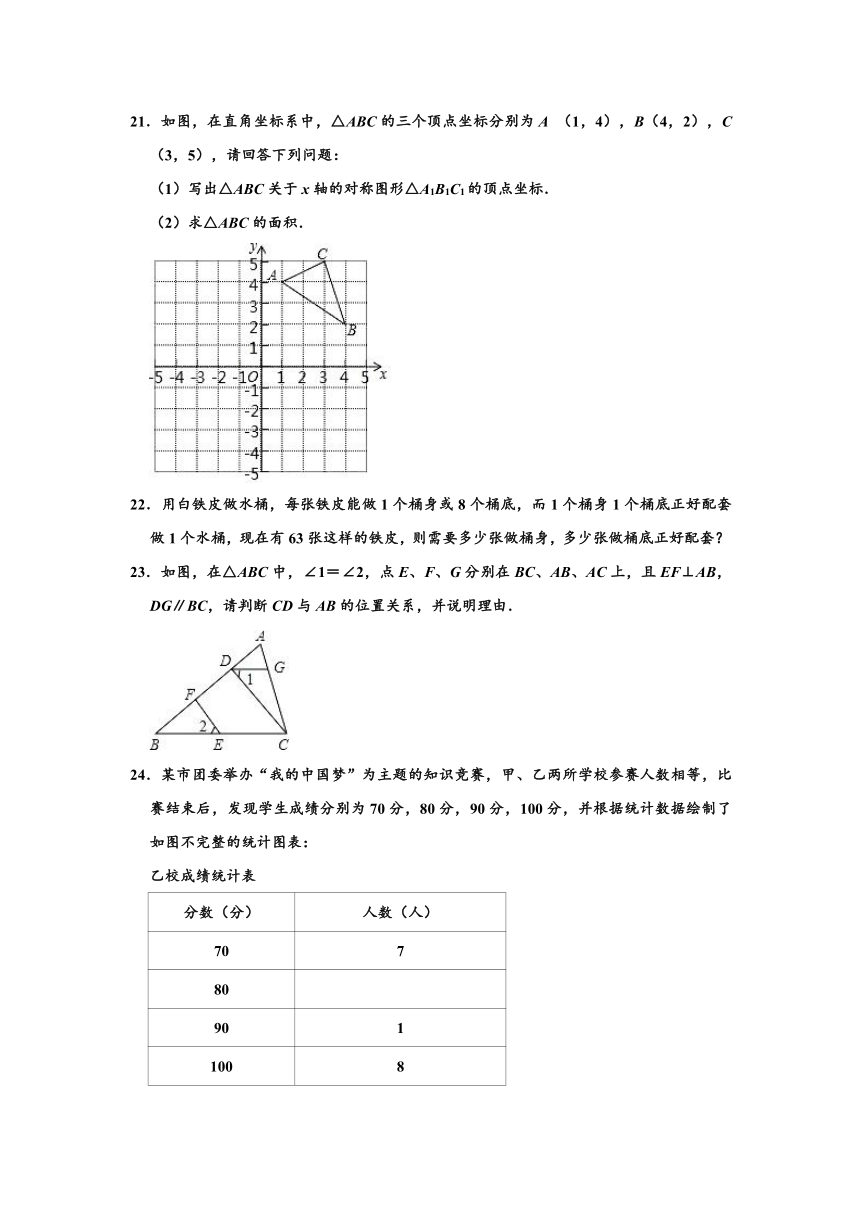
21.如图,在直角坐标系中,△ABC的三个顶点坐标分别为A
(1,4),B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.
(2)求△ABC的面积.
22.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底,而1个桶身1个桶底正好配套做1个水桶,现在有63张这样的铁皮,则需要多少张做桶身,多少张做桶底正好配套?
23.如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
24.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为
;在图②中,“100分”的有
人;
(2)甲校成绩的中位数为
;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
25.A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是
(填l1或l2);甲的速度是
km/h,乙的速度是
km/h;
(2)甲出发多少小时两人恰好相距5km?
参考答案
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.4
B.±4
C.±2
D.2
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:=4,4的平方根是±2.
故选:C.
2.已知以下三个数,不能组成直角三角形的是( )
A.9、12、15
B.、3、2
C.0.3、0.4、0.5
D.32、42、52
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解:A、92+122=152,能构成直角三角形,故不符合题意;
B、()2+32=(2)2,能构成直角三角形,故不符合题意;
C、0.32+0.42=0.52,能构成直角三角形,故不符合题意;
D、(32)2+(42)2≠(52)2,不能构成直角三角形,故符合题意;
故选:D.
3.如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(﹣2,0)
B.(0,﹣2)
C.(1,0)
D.(0,1)
【分析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,
解得m=﹣3,2m+4=﹣2,
∴点P的坐标是(0,﹣2).
故选:B.
4.已知a,b为两个连续的整数,且a<<b,则ba=( )
A.1
B.2
C.6
D.9
【分析】直接利用的取值范围得出a,b的值,即可得出答案.
解:∵a,b为两个连续的整数,且a<<b,
∴a=2,b=3,
∴ba=32=9.
故选:D.
5.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】此题可解出的x、y的值,然后根据x、y的值可以判断出该点在何象限内.
解:根据题意,
可知﹣x+2=x﹣1,
∴x=,
∴y=.
∵x>0,y>0,
∴该点坐标在第一象限.
故选:A.
6.若函数y=(m+1)x|m|+2是一次函数,则m的值为( )
A.m=±1
B.m=﹣1
C.m=1
D.m≠﹣1
【分析】根据一次函数的定义可列方程:|m|=1,m+1≠0,继而即可求出m的值.
解:根据次函数的定义可知:|m|=1,m+1≠0,
解得:m=1.
故选:C.
7.二元一次方程x+2y=9的所有正整数解有( )
A.1个
B.2个
C.3个
D.4个
【分析】把y看做已知数求出x,即可确定出正整数解.
解:方程x+2y=9,
解得:x=﹣2y+9,
当y=1时,x=7;y=2时,x=5;y=3时,x=3;y=4时,x=1,
则方程的正整数解为4个,
故选:D.
8.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β﹣∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α,∠2=180°﹣∠β,于是得到结论.
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α,∠2=180°﹣∠β,
∵∠BCD=90°,
∴∠1+∠2=∠α+180°﹣∠β=90°,
∴∠β﹣∠α=90°,
故选:B.
9.某车间20名工人日加工零件数如表所示:这些工人日加工零件数的众数、中位数、平均数分别是( )
日加工零件数
4
5
6
7
8
人数
2
6
5
4
3
A.5、6、5
B.5、5、6
C.6、5、6
D.5、6、6
【分析】根据众数、平均数和中位数的定义分别进行解答即可.
解:5出现了6次,出现的次数最多,则众数是5;
把这些数从小到大排列,中位数第10、11个数的平均数,
则中位数=6,
平均数是×(4×2+5×6+6×5+7×4+8×3)=6,
故选:D.
10.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )
A.
B.
C.
D.
【分析】直接根据一次函数与系数的关系进行判断.
解:∵k<0,b<0,
∴一次函数图象在二、三、四象限.
故选:B.
二、填空题(每小题3分,共24分)
11.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是 ﹣3
【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”求出a、b的值,然后相加计算即可得解.
解:∵点M(a,﹣1)与点N(2,b)关于y轴对称,
∴a=﹣2,b=﹣1,
∴a+b=(﹣2)+(﹣1)=﹣3.
故答案为:﹣3.
12.计算:(﹣2)2019×(+2)2020= ﹣2﹣ .
【分析】直接利用积的乘方运算法则化简得出答案.
解:原式=[(﹣2)×(+2)]2019×(+2)
=﹣2﹣.
故答案为:﹣2﹣.
13.已知直角三角形的两直角边长分别是3,4,则它的周长为 12 .
【分析】根据勾股定理求出斜边长,根据三角形的周长公式计算即可.
解:由勾股定理得,直角三角形的斜边长==5,
则三角形的周长=3+4+5=12,
故答案为:12.
14.若关于x、y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为 .
【分析】先用含k的代数式表示x、y,即解关于x,y的方程组,再代入2x+3y=6中可得.
解:根据题意组,得,x=7k,y=﹣2k,
把x,y代入二元一次方程2x+3y=﹣6,
得:2×7k+3×(﹣2k)=6,
.
故答案为:
15.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是 乙 (填“甲”或“乙”).
【分析】根据方差的定义,方差越小数据越稳定即可得出答案.
解:∵S甲2=0.2,S乙2=0.08,
∴S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
16.已知关于x的一次函数y=mx+n的图象如图所示,则可化简为 n .
【分析】根据一次函数图象与系数的关系,确定m、n的符号,然后由绝对值、二次根式的化简运算法则解得即可.
解:根据图示知,关于x的一次函数y=mx+n的图象经过第一、二、四象限,
∴m<0;
又∵关于x的一次函数y=mx+n的图象与y轴交于正半轴,
∴n>0;
∴=n﹣m﹣(﹣m)=n.
故答案是:n.
17.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 25° .
【分析】根据两直线平行,内错角相等求出∠3的内错角,再根据三角板的度数求差即可得解.
解:∵直尺的对边平行,∠1=20°,
∴∠3=∠1=20°,
∴∠2=45°﹣∠3=45°﹣20°=25°.
故答案为:25°.
18.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 x>2 .
【分析】根据一次函数的图象可直接进行解答.
解:由函数图象可知,此函数是减函数,当y=3时x=2,
故当y<3时,x>2.
故答案为:x>2.
三、解答题.(共46分)
19.计算:÷﹣×+(﹣)﹣1.
【分析】根据二次根式的乘除法法则和负整数指数幂进行解答即可.
解:÷﹣×+(﹣)﹣1.
=
=4﹣
=.
20.解方程组.
【分析】先将②两边都乘以3再减①求出t,再代入②求出s.
解:,
②×3﹣①得:
3s+12t﹣(3s﹣5t)=﹣45﹣6,
17t=﹣51,
t=﹣3,
把t=﹣3代入②得:
s=﹣3,
∴.
21.如图,在直角坐标系中,△ABC的三个顶点坐标分别为A
(1,4),B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.
(2)求△ABC的面积.
【分析】(1)依据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即可得出△A1B1C1的顶点坐标.
(2)依据割补法进行计算,即可得出△ABC的面积.
解:(1)△ABC关于x轴的对称图形△A1B1C1的顶点坐标为:
A1(1,﹣4),B1(4,﹣2),C1(3,﹣5).
(2)△ABC的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=9﹣1﹣1.5﹣3=3.5.
22.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底,而1个桶身1个桶底正好配套做1个水桶,现在有63张这样的铁皮,则需要多少张做桶身,多少张做桶底正好配套?
【分析】本题的等量关系为:桶身所用铁皮张数+桶底所用铁皮张数=63;桶身数=桶底数.
解:设用x张铁皮做桶身,y张铁皮做桶底,
根据题意得:
解得:
答:需要用56张铁皮做桶身,7张铁皮做桶底.
23.如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
【分析】由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
24.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为 54° ;在图②中,“100分”的有 5 人;
(2)甲校成绩的中位数为 90分 ;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
【分析】(1)甲校得“70分”的有6人,占调查人数的30%,可求出调查人数,“100分”的人数,以及“80分”的所占的百分比和圆心角度数;
(2)根据中位数的意义,找出处在第10、11位的两个数的平均数即可;
(3)求出乙校得“80分”的人数,利用加权平均数的计算方法进行计算即可;
(4)从方差的大小,得出数据的离散程度.
解:(1)6÷30%=20(人),360°×=54°,20﹣6﹣3﹣6=5(人),
故答案为:54°,5;
(2)将甲校的成绩从小到大排列后,处在第10、11位的两个数都是90分,因此中位数是90分,
故答案为:90分;
(3)20﹣7﹣1﹣8=4(人)
==85(分),
答:乙校的平均成绩为85分;
(4)∵S甲2=135<S乙2=175,
∴甲校的成绩离散程度较小,比较稳定.
25.A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 l2 (填l1或l2);甲的速度是 30 km/h,乙的速度是 20 km/h;
(2)甲出发多少小时两人恰好相距5km?
【分析】(1)观察图象即可知道乙的函数图象为l2,根据速度=,利用图中信息即可解决问题;
(2)分相遇前或相遇后两种情形分别列出方程即可解决问题;
解:(1)由题意可知,乙的函数图象是l2,
甲的速度是=30km/h,乙的速度是=20km/h.
故答案为l2,30,20.
(2)设甲出发x小时两人恰好相距5km.
由题意30x+20(x﹣0.5)+5=60或30x+20(x﹣0.5)﹣5=60
解得x=1.3或1.5,
答:甲出发1.3小时或1.5小时两人恰好相距5km.
一、选择题(共10小题).
1.的平方根是( )
A.4
B.±4
C.±2
D.2
2.已知以下三个数,不能组成直角三角形的是( )
A.9、12、15
B.、3、2
C.0.3、0.4、0.5
D.32、42、52
3.如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(﹣2,0)
B.(0,﹣2)
C.(1,0)
D.(0,1)
4.已知a,b为两个连续的整数,且a<<b,则ba=( )
A.1
B.2
C.6
D.9
5.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.若函数y=(m+1)x|m|+2是一次函数,则m的值为( )
A.m=±1
B.m=﹣1
C.m=1
D.m≠﹣1
7.二元一次方程x+2y=9的所有正整数解有( )
A.1个
B.2个
C.3个
D.4个
8.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β﹣∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
9.某车间20名工人日加工零件数如表所示:这些工人日加工零件数的众数、中位数、平均数分别是( )
日加工零件数
4
5
6
7
8
人数
2
6
5
4
3
A.5、6、5
B.5、5、6
C.6、5、6
D.5、6、6
10.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
11.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是
12.计算:(﹣2)2019×(+2)2020=
.
13.已知直角三角形的两直角边长分别是3,4,则它的周长为
.
14.若关于x、y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为
.
15.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是
(填“甲”或“乙”).
16.已知关于x的一次函数y=mx+n的图象如图所示,则可化简为
.
17.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是
.
18.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
.
三、解答题.(共46分)
19.计算:÷﹣×+(﹣)﹣1.
20.解方程组.
21.如图,在直角坐标系中,△ABC的三个顶点坐标分别为A
(1,4),B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.
(2)求△ABC的面积.
22.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底,而1个桶身1个桶底正好配套做1个水桶,现在有63张这样的铁皮,则需要多少张做桶身,多少张做桶底正好配套?
23.如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
24.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为
;在图②中,“100分”的有
人;
(2)甲校成绩的中位数为
;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
25.A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是
(填l1或l2);甲的速度是
km/h,乙的速度是
km/h;
(2)甲出发多少小时两人恰好相距5km?
参考答案
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.4
B.±4
C.±2
D.2
【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.
解:=4,4的平方根是±2.
故选:C.
2.已知以下三个数,不能组成直角三角形的是( )
A.9、12、15
B.、3、2
C.0.3、0.4、0.5
D.32、42、52
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解:A、92+122=152,能构成直角三角形,故不符合题意;
B、()2+32=(2)2,能构成直角三角形,故不符合题意;
C、0.32+0.42=0.52,能构成直角三角形,故不符合题意;
D、(32)2+(42)2≠(52)2,不能构成直角三角形,故符合题意;
故选:D.
3.如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(﹣2,0)
B.(0,﹣2)
C.(1,0)
D.(0,1)
【分析】根据点在y轴上,可知P的横坐标为0,即可得m的值,再确定点P的坐标即可.
解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,
解得m=﹣3,2m+4=﹣2,
∴点P的坐标是(0,﹣2).
故选:B.
4.已知a,b为两个连续的整数,且a<<b,则ba=( )
A.1
B.2
C.6
D.9
【分析】直接利用的取值范围得出a,b的值,即可得出答案.
解:∵a,b为两个连续的整数,且a<<b,
∴a=2,b=3,
∴ba=32=9.
故选:D.
5.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】此题可解出的x、y的值,然后根据x、y的值可以判断出该点在何象限内.
解:根据题意,
可知﹣x+2=x﹣1,
∴x=,
∴y=.
∵x>0,y>0,
∴该点坐标在第一象限.
故选:A.
6.若函数y=(m+1)x|m|+2是一次函数,则m的值为( )
A.m=±1
B.m=﹣1
C.m=1
D.m≠﹣1
【分析】根据一次函数的定义可列方程:|m|=1,m+1≠0,继而即可求出m的值.
解:根据次函数的定义可知:|m|=1,m+1≠0,
解得:m=1.
故选:C.
7.二元一次方程x+2y=9的所有正整数解有( )
A.1个
B.2个
C.3个
D.4个
【分析】把y看做已知数求出x,即可确定出正整数解.
解:方程x+2y=9,
解得:x=﹣2y+9,
当y=1时,x=7;y=2时,x=5;y=3时,x=3;y=4时,x=1,
则方程的正整数解为4个,
故选:D.
8.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β﹣∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
【分析】过C作CF∥AB,根据平行线的性质得到∠1=∠α,∠2=180°﹣∠β,于是得到结论.
解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α,∠2=180°﹣∠β,
∵∠BCD=90°,
∴∠1+∠2=∠α+180°﹣∠β=90°,
∴∠β﹣∠α=90°,
故选:B.
9.某车间20名工人日加工零件数如表所示:这些工人日加工零件数的众数、中位数、平均数分别是( )
日加工零件数
4
5
6
7
8
人数
2
6
5
4
3
A.5、6、5
B.5、5、6
C.6、5、6
D.5、6、6
【分析】根据众数、平均数和中位数的定义分别进行解答即可.
解:5出现了6次,出现的次数最多,则众数是5;
把这些数从小到大排列,中位数第10、11个数的平均数,
则中位数=6,
平均数是×(4×2+5×6+6×5+7×4+8×3)=6,
故选:D.
10.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )
A.
B.
C.
D.
【分析】直接根据一次函数与系数的关系进行判断.
解:∵k<0,b<0,
∴一次函数图象在二、三、四象限.
故选:B.
二、填空题(每小题3分,共24分)
11.若点M(a,﹣1)与点N(2,b)关于y轴对称,则a+b的值是 ﹣3
【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”求出a、b的值,然后相加计算即可得解.
解:∵点M(a,﹣1)与点N(2,b)关于y轴对称,
∴a=﹣2,b=﹣1,
∴a+b=(﹣2)+(﹣1)=﹣3.
故答案为:﹣3.
12.计算:(﹣2)2019×(+2)2020= ﹣2﹣ .
【分析】直接利用积的乘方运算法则化简得出答案.
解:原式=[(﹣2)×(+2)]2019×(+2)
=﹣2﹣.
故答案为:﹣2﹣.
13.已知直角三角形的两直角边长分别是3,4,则它的周长为 12 .
【分析】根据勾股定理求出斜边长,根据三角形的周长公式计算即可.
解:由勾股定理得,直角三角形的斜边长==5,
则三角形的周长=3+4+5=12,
故答案为:12.
14.若关于x、y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为 .
【分析】先用含k的代数式表示x、y,即解关于x,y的方程组,再代入2x+3y=6中可得.
解:根据题意组,得,x=7k,y=﹣2k,
把x,y代入二元一次方程2x+3y=﹣6,
得:2×7k+3×(﹣2k)=6,
.
故答案为:
15.甲、乙两名男同学练习投掷实心球,每人投了10次,平均成绩均为7.5米,方差分别为s甲2=0.2,S乙2=0.08,成绩比较稳定的是 乙 (填“甲”或“乙”).
【分析】根据方差的定义,方差越小数据越稳定即可得出答案.
解:∵S甲2=0.2,S乙2=0.08,
∴S甲2>S乙2,
∴成绩比较稳定的是乙;
故答案为:乙.
16.已知关于x的一次函数y=mx+n的图象如图所示,则可化简为 n .
【分析】根据一次函数图象与系数的关系,确定m、n的符号,然后由绝对值、二次根式的化简运算法则解得即可.
解:根据图示知,关于x的一次函数y=mx+n的图象经过第一、二、四象限,
∴m<0;
又∵关于x的一次函数y=mx+n的图象与y轴交于正半轴,
∴n>0;
∴=n﹣m﹣(﹣m)=n.
故答案是:n.
17.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 25° .
【分析】根据两直线平行,内错角相等求出∠3的内错角,再根据三角板的度数求差即可得解.
解:∵直尺的对边平行,∠1=20°,
∴∠3=∠1=20°,
∴∠2=45°﹣∠3=45°﹣20°=25°.
故答案为:25°.
18.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 x>2 .
【分析】根据一次函数的图象可直接进行解答.
解:由函数图象可知,此函数是减函数,当y=3时x=2,
故当y<3时,x>2.
故答案为:x>2.
三、解答题.(共46分)
19.计算:÷﹣×+(﹣)﹣1.
【分析】根据二次根式的乘除法法则和负整数指数幂进行解答即可.
解:÷﹣×+(﹣)﹣1.
=
=4﹣
=.
20.解方程组.
【分析】先将②两边都乘以3再减①求出t,再代入②求出s.
解:,
②×3﹣①得:
3s+12t﹣(3s﹣5t)=﹣45﹣6,
17t=﹣51,
t=﹣3,
把t=﹣3代入②得:
s=﹣3,
∴.
21.如图,在直角坐标系中,△ABC的三个顶点坐标分别为A
(1,4),B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.
(2)求△ABC的面积.
【分析】(1)依据关于x轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数,即可得出△A1B1C1的顶点坐标.
(2)依据割补法进行计算,即可得出△ABC的面积.
解:(1)△ABC关于x轴的对称图形△A1B1C1的顶点坐标为:
A1(1,﹣4),B1(4,﹣2),C1(3,﹣5).
(2)△ABC的面积为:3×3﹣×1×2﹣×1×3﹣×2×3=9﹣1﹣1.5﹣3=3.5.
22.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底,而1个桶身1个桶底正好配套做1个水桶,现在有63张这样的铁皮,则需要多少张做桶身,多少张做桶底正好配套?
【分析】本题的等量关系为:桶身所用铁皮张数+桶底所用铁皮张数=63;桶身数=桶底数.
解:设用x张铁皮做桶身,y张铁皮做桶底,
根据题意得:
解得:
答:需要用56张铁皮做桶身,7张铁皮做桶底.
23.如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
【分析】由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
24.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为 54° ;在图②中,“100分”的有 5 人;
(2)甲校成绩的中位数为 90分 ;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
【分析】(1)甲校得“70分”的有6人,占调查人数的30%,可求出调查人数,“100分”的人数,以及“80分”的所占的百分比和圆心角度数;
(2)根据中位数的意义,找出处在第10、11位的两个数的平均数即可;
(3)求出乙校得“80分”的人数,利用加权平均数的计算方法进行计算即可;
(4)从方差的大小,得出数据的离散程度.
解:(1)6÷30%=20(人),360°×=54°,20﹣6﹣3﹣6=5(人),
故答案为:54°,5;
(2)将甲校的成绩从小到大排列后,处在第10、11位的两个数都是90分,因此中位数是90分,
故答案为:90分;
(3)20﹣7﹣1﹣8=4(人)
==85(分),
答:乙校的平均成绩为85分;
(4)∵S甲2=135<S乙2=175,
∴甲校的成绩离散程度较小,比较稳定.
25.A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 l2 (填l1或l2);甲的速度是 30 km/h,乙的速度是 20 km/h;
(2)甲出发多少小时两人恰好相距5km?
【分析】(1)观察图象即可知道乙的函数图象为l2,根据速度=,利用图中信息即可解决问题;
(2)分相遇前或相遇后两种情形分别列出方程即可解决问题;
解:(1)由题意可知,乙的函数图象是l2,
甲的速度是=30km/h,乙的速度是=20km/h.
故答案为l2,30,20.
(2)设甲出发x小时两人恰好相距5km.
由题意30x+20(x﹣0.5)+5=60或30x+20(x﹣0.5)﹣5=60
解得x=1.3或1.5,
答:甲出发1.3小时或1.5小时两人恰好相距5km.
同课章节目录
