2019-2020学年黑龙江省哈尔滨市“五校协作体”七年级下学期期末数学试卷(五四学制) (解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市“五校协作体”七年级下学期期末数学试卷(五四学制) (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 538.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 07:03:59 | ||
图片预览



文档简介
2019-2020学年七年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列方程是二元一次方程的是( )
A.2x﹣y=1
B.x2﹣2x+1=0
C.2x﹣1=0
D.x﹣3=2x
2.如果方程x=1与2x+a=ax的解相同,则a的值是( )
A.2
B.﹣2
C.3
D.﹣3
3.甲、乙两台机床生产一种零件,在10天中两台机床每天生产的次品数的平均数是==2,方差是:S甲2=1.65,S乙2=0.76,出次品的波动较小的机床是( )
A.甲机床
B.乙机床
C.甲、乙机床一样
D.不能确定
4.下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
5.为了预防新冠病毒,6名学生准备了口罩,口罩数量(单位:个)分别为:87、88、73、88、79、85,这组数据的众数是( )
A.79
B.87
C.88
D.85
6.不等式组的解集是( )
A.x≤﹣1
B.x≥3
C.﹣3≤x≤1
D.﹣3≤x<1
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm
B.5cm
C.6cm
D.7cm
8.△ABC中,它的三条角平分线的交点为O,若∠B=80°,则∠AOC的度数为( )
A.100°
B.130°
C.110°
D.150°
9.如图,△ADM中,AM=DM,∠AMD=90°,直线l经过点M,AB⊥l,DC⊥l,垂足分别为B,C,若AB=2,CD=5,则BC的长度为( )
A.1.5
B.3
C.4
D.5
10.下列说法中,正确的个数为( )
①三角形的外角等于两个内角的和;②有两边和一角分别相等的两个三角形全等;③各边都相等的多边形是正多边形;④到角两边距离相等的点,在这个角的平分线上.
A.1
B.2
C.3
D.0
二、填空题(每小题3分,共计30分)
11.把方程7x﹣y=15改写成用含x的式子表示y的形式为y=
.
12.“x的2倍与3的和不大于5”用不等式表示是
.
13.五边形的内角和为
度.
14.已知a、b满足方程组,则a+b的值为
.
15.若关于x的不等式(m﹣l)x<m﹣1的解集为x>1,则m的取值范围是
.
16.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中,要测量工件内槽宽AB,只要测
就可以了.
17.若一等腰三角形的两边长分别为3cm、7cm,则该三角形的周长为
.
18.如图,A,B分别是线段OC,OD上的点,OC=OD,OA=OB,若∠O=60°,∠C=25°,则∠BED的度数是
度.
19.在△ABC中,AD,AE分别是它的高线,角平分线,当∠B=40°,∠ACD=60°,则∠EAD的度数为
度.
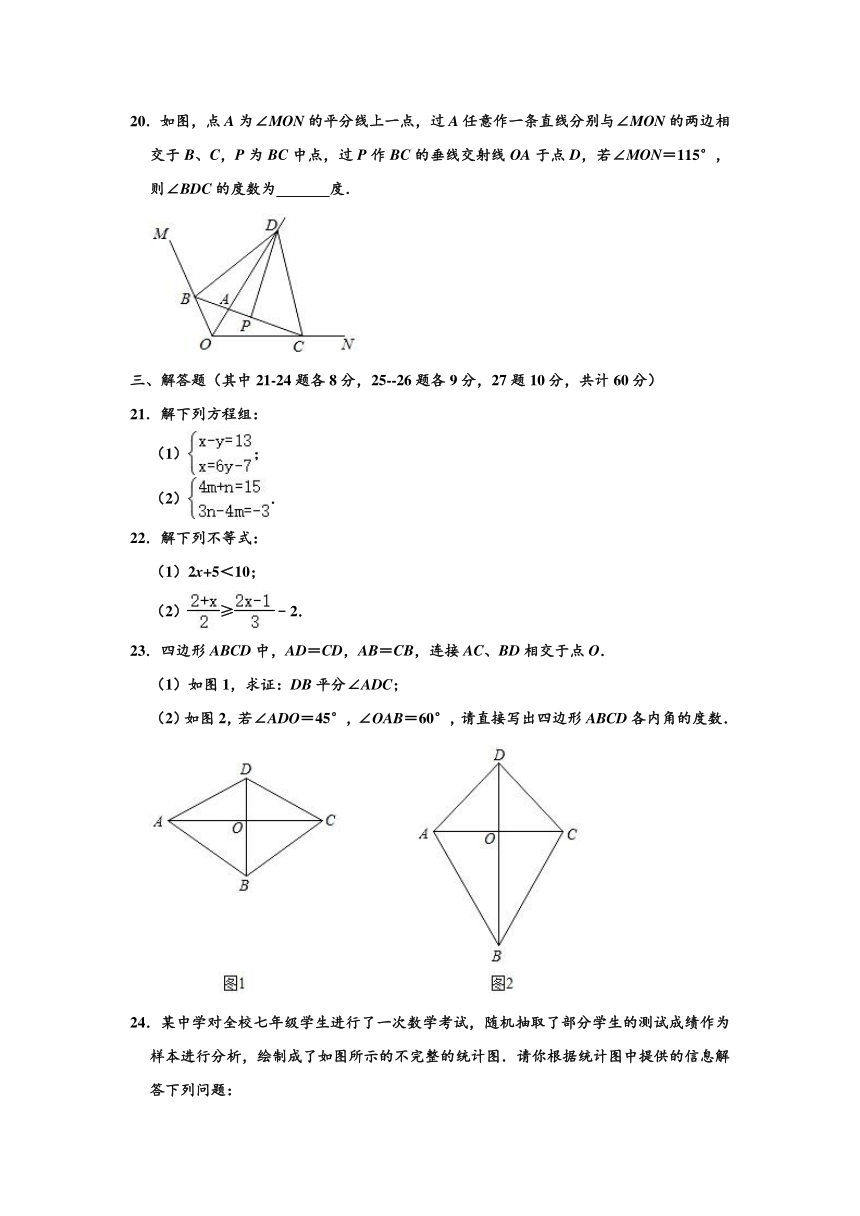
20.如图,点A为∠MON的平分线上一点,过A任意作一条直线分别与∠MON的两边相交于B、C,P为BC中点,过P作BC的垂线交射线OA于点D,若∠MON=115°,则∠BDC的度数为
度.
三、解答题(其中21-24题各8分,25--26题各9分,27题10分,共计60分)
21.解下列方程组:
(1);
(2).
22.解下列不等式:
(1)2x+5<10;
(2)≥﹣2.
23.四边形ABCD中,AD=CD,AB=CB,连接AC、BD相交于点O.
(1)如图1,求证:DB平分∠ADC;
(2)如图2,若∠ADO=45°,∠OAB=60°,请直接写出四边形ABCD各内角的度数.
24.某中学对全校七年级学生进行了一次数学考试,随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的不完整的统计图.请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;并直接写出这部分学生成绩的中位数落在哪组?
(3)如果该学校七年级共有380人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀.
25.疫情爆发,物资紧缺,一医药集团主动担当作为,紧急投产口罩生产线,每天生产医用防护口罩或者医用外科口罩.已知2天生产医用防护口罩、1天生产医用外科口罩,可生产两种口罩共8万只;若1天生产医用防护口罩、3天生产医用外科口罩,可生产两种口罩共9万只.
(1)求平均每天生产医用防护口罩和医用外科口罩各多少万只?
(2)该集团现接到需要180万只口罩的订单,要求生产时间不能超过70天,则工厂至少能生产多少万只医用防护口罩?
26.已知:Rt△ABC中,∠CAB=90°,CA=BA,Rt△ADE中,∠DAE=90°,DA=EA,连接CE、BD.
(1)如图1,求证:CE=BD;
(2)如图2,当D在AC上,E在BA的延长线上,直线BD、CE相交于点F,求证:CE⊥BD;
(3)如图3,在(2)的条件下,若D是AC中点,BF=6,求△BEF的面积.
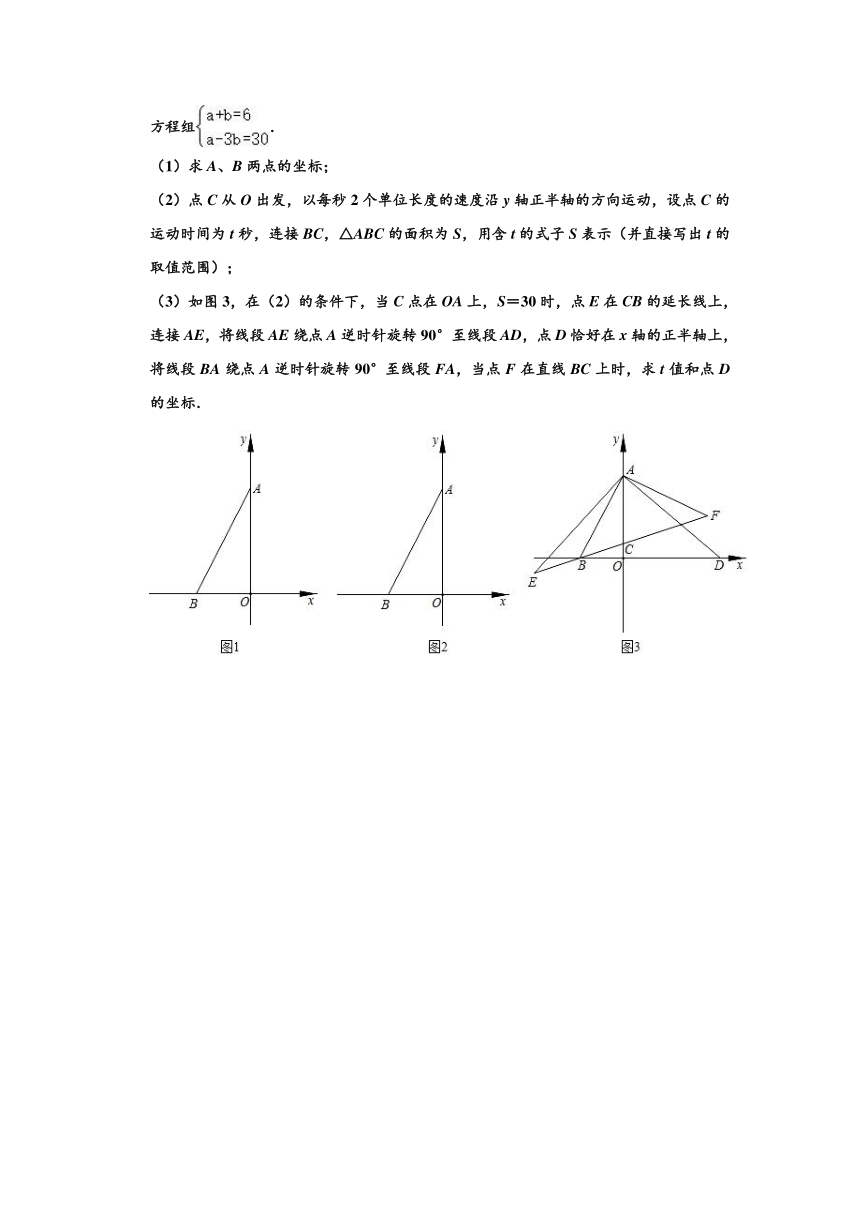
27.如图,在平面直角坐标系中,点O为原点,A(0,a),B(b,0),已知a、b满足方程组.
(1)求A、B两点的坐标;
(2)点C从O出发,以每秒2个单位长度的速度沿y轴正半轴的方向运动,设点C的运动时间为t秒,连接BC,△ABC的面积为S,用含t的式子S表示(并直接写出t的取值范围);
(3)如图3,在(2)的条件下,当C点在OA上,S=30时,点E在CB的延长线上,连接AE,将线段AE绕点A逆时针旋转90°至线段AD,点D恰好在x轴的正半轴上,将线段BA绕点A逆时针旋转90°至线段FA,当点F在直线BC上时,求t值和点D的坐标.
参考答案
一、选择题(每小题3分,共计30分)
1.下列方程是二元一次方程的是( )
A.2x﹣y=1
B.x2﹣2x+1=0
C.2x﹣1=0
D.x﹣3=2x
【分析】根据二元一次方程的定义逐个判断即可.
解:A、是二元一次方程,故本选项符合题意;
B、是一元二次方程,不是二元一次方程,故本选项不符合题意;
C、是一元一次方程,不是二元一次方程,故本选项不符合题意;
D、是一元一次方程,不是二元一次方程,故本选项不符合题意;
故选:A.
2.如果方程x=1与2x+a=ax的解相同,则a的值是( )
A.2
B.﹣2
C.3
D.﹣3
【分析】可以分别解出两方程的解,两解相等,就得到关于a的方程,从而可以求出a的值.
解:解第一个方程得:x=3,
解第二个方程得:x=
∴=3
解得:a=3
故选:C.
3.甲、乙两台机床生产一种零件,在10天中两台机床每天生产的次品数的平均数是==2,方差是:S甲2=1.65,S乙2=0.76,出次品的波动较小的机床是( )
A.甲机床
B.乙机床
C.甲、乙机床一样
D.不能确定
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解:∵S甲2=1.65,S乙2=0.76,
∴S甲2>S乙2,
∴出次品的波动较小的机床是乙机床;
故选:B.
4.下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
【分析】稳定性是三角形的特性.
解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
5.为了预防新冠病毒,6名学生准备了口罩,口罩数量(单位:个)分别为:87、88、73、88、79、85,这组数据的众数是( )
A.79
B.87
C.88
D.85
【分析】根据众数的概念求解可得.
解:这组数据的众数为88,
故选:C.
6.不等式组的解集是( )
A.x≤﹣1
B.x≥3
C.﹣3≤x≤1
D.﹣3≤x<1
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解:解不等式x+3≥0,得:x≥﹣3,
解不等式3x﹣1≤2,得:x≤1,
则不等式组的解集为﹣3≤x≤1.
故选:C.
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm
B.5cm
C.6cm
D.7cm
【分析】根据全等三角形的性质求出DE=EC,求出AE+DE=AC,即可求出答案.
解:∵DE⊥AB于D,
∴∠BDE=90°,
在Rt△BDE和Rt△BCE中,
,
∴Rt△BDE≌Rt△BCE(HL),
∴ED=CE,
∴AE+ED=AE+CE=AC=6cm,
故选:C.
8.△ABC中,它的三条角平分线的交点为O,若∠B=80°,则∠AOC的度数为( )
A.100°
B.130°
C.110°
D.150°
【分析】先根据三角形的内角和定理求出∠BAC+∠BCA的度数,再根据角平分线的定义求出(∠BAC+∠BCA),然后再利用三角形的内角和定理求解即可.
解:∵AO,CO分别是∠BAC,∠BCA的平分线,
∴∠OAC=∠BAC,∠OCA=∠BCA,
∴∠AOC=180°﹣∠OAC﹣∠OCA
=180°﹣∠BAC﹣∠BCA,
=180°﹣(∠BAC+∠BCA).
又∵∠B=80°,
∴∠BAC+∠BCA=180°﹣80°=100°.
∴(∠BAC+∠BCA)=100°×=50°.
∴∠AOC=180°﹣50°=130°,
故选:B.
9.如图,△ADM中,AM=DM,∠AMD=90°,直线l经过点M,AB⊥l,DC⊥l,垂足分别为B,C,若AB=2,CD=5,则BC的长度为( )
A.1.5
B.3
C.4
D.5
【分析】根据全等三角形的判定和性质得出AB=CM,CD=BM,进而解答即可.
解:∵AB⊥l,DC⊥l,
∴∠DCM=∠MBA=90°,∠MDC+∠DMC=90°,
∵∠AMD=90°,
∴∠DMC+∠AMB=90°,
∴∠MDC=∠AMB,
在△DMC与△MAB中
,
∴△DMC≌△MAB(AAS),
∴AB=CM=2,CD=BM=5,
∴BC=BM﹣CM=5﹣2=3,
故选:B.
10.下列说法中,正确的个数为( )
①三角形的外角等于两个内角的和;②有两边和一角分别相等的两个三角形全等;③各边都相等的多边形是正多边形;④到角两边距离相等的点,在这个角的平分线上.
A.1
B.2
C.3
D.0
【分析】根据三角形的外角的性质,全等三角形的判定,正多边形的定义,角平分线的判定定理一一判断即可.
解:①三角形的外角等于两个内角的和,错误,应该是三角形的外角等于和它不相邻两个内角的和.
②有两边和一角分别相等的两个三角形全等,错误,应该是有两边和夹角分别相等的两个三角形全等.
③各边都相等的多边形是正多边形,错误.缺少各个角相等这个条件.
④到角两边距离相等的点,在这个角的平分线上.错误,这个点必须在这个角的内部.
故选:D.
二、填空题(每小题3分,共计30分)
11.把方程7x﹣y=15改写成用含x的式子表示y的形式为y= 7x﹣15 .
【分析】将x看做已知数求出y即可.
解:∵7x﹣y=15,
∴y=7x﹣15,
故答案为:7x﹣15.
12.“x的2倍与3的和不大于5”用不等式表示是 2x+3≤5 .
【分析】首先表示“x的2倍”为2x,再表示“与3的和”为2x+3,最后表示“不大于5”可得2x+3≤5.
解:由题意得:2x+3≤5,
故答案为2x+3≤5.
13.五边形的内角和为 540 度.
【分析】n边形内角和公式为(n﹣2)180°,把n=5代入可求五边形内角和.
解:五边形的内角和为(5﹣2)×180°=540°.
故答案为:540.
14.已知a、b满足方程组,则a+b的值为 5 .
【分析】求出方程组的解得到a与b的值,即可确定出a+b的值.
解:,
①+②得:4a+4b=20,
即4(a+b)=20,
解得a+b=5.
故答案为:5.
15.若关于x的不等式(m﹣l)x<m﹣1的解集为x>1,则m的取值范围是 m<1 .
【分析】根据不等式的基本性质3,两边都除以m﹣1后得到x>1,可知m﹣1<0,解之可得.
解:∵将不等式(m﹣1)x<m﹣1两边都除以(m﹣1),得x>1,
∴m﹣1<0,
解得:m<1,
故答案为m<1.
16.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中,要测量工件内槽宽AB,只要测 A'B' 就可以了.
【分析】让我们了解测量两点之间的距离,只要符合全等三角形全等的条件之一SAS,只需要测量易测量的边A'B'上.测量方案的操作性强.
解:答:只要测量A'B'.
理由:连接AB,A'B',如图,
∵点O分别是AC、BB'的中点,
∴OA=OA',OB=OB'.
在△AOB和△A'OB'中,
OA=OA',∠AOB=∠A'OB'(对顶角相等),OB=OB',
∴△AOB≌△A'OB'(SAS).
∴A'B'=AB.
答:需要测量A'B'的长度,即为工件内槽宽AB,
故答案为:A'B'
17.若一等腰三角形的两边长分别为3cm、7cm,则该三角形的周长为 17cm .
【分析】题中没有指出哪个底哪个是腰,故应该分情况进行分析,注意应用三角形三边关系进行验证能否组成三角形.
解:当3cm是腰时,3+3<7,不符合三角形三边关系,故舍去;
当7cm是腰时,周长=7+7+3=17cm.
故它的周长为17cm.
故答案为:17cm.
18.如图,A,B分别是线段OC,OD上的点,OC=OD,OA=OB,若∠O=60°,∠C=25°,则∠BED的度数是 70 度.
【分析】证△ODA≌△OCB,推出∠D=∠C=25°,根据三角形外角性质求出∠DBE,根据三角形内角和定理求出即可.
解:在△ODA和△OCB中
,
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180°﹣85°﹣25°=70°,
故答案为:70.
19.在△ABC中,AD,AE分别是它的高线,角平分线,当∠B=40°,∠ACD=60°,则∠EAD的度数为 10或40 度.
【分析】由三角形内角和可求得∠BAC,则由角平分线的定义可求得∠BAE,在Rt△BAD中,可求得∠BAD,则可求得∠EAD.
解:当高AD在△ABC的内部时.
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣40°﹣60°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=90°﹣∠B=50°,
∴∠EAD=∠BAD﹣∠BAE=50°﹣40°=10°.
当高AD在△ABC的外部时.
同法可得∠EAD=10°+30°=40°
故答案为10或40.
20.如图,点A为∠MON的平分线上一点,过A任意作一条直线分别与∠MON的两边相交于B、C,P为BC中点,过P作BC的垂线交射线OA于点D,若∠MON=115°,则∠BDC的度数为 65 度.
【分析】过D作DE⊥OM于E,DF⊥ON于F,求出∠EDF,根据角平分线性质求出DE=DF,根据线段垂直平分线性质求出BD=CD,证Rt△DEB≌Rt△DFC,求出∠EDB=∠CDF,推出∠BDC=∠EDF,即可得出答案.
解:如图:过D作DE⊥OM于E,DF⊥ON于F,
则∠DEB=∠DFC=∠DFO=90°,
∵∠MON=115°,
∴∠EDF=360°﹣90°﹣90°﹣115°=65°,
∵DE⊥OM,DF⊥ON,OD∠MON,
∴DE=DF,
∵P为BC中点,DP⊥BC,
∴BD=CD,
在Rt△DEB和Rt△DFC中,,
∴Rt△DEB≌Rt△DFC(HL),
∴∠EDB=∠CDF,
∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=65°.
故答案为:65.
三、解答题(其中21-24题各8分,25--26题各9分,27题10分,共计60分)
21.解下列方程组:
(1);
(2).
【分析】(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解:(1),
把②代入①得:6y﹣7﹣y=13,
解得:y=4,
把y=4代入①得:x=17,
则方程组的解为;
(2),
①+②得:4n=12,
解得:n=3,
把n=3代入①得:m=3,
则方程组的解为.
22.解下列不等式:
(1)2x+5<10;
(2)≥﹣2.
【分析】(1)移项、合并同类项,然后系数化成1即可求解;
(2)去分母、去括号、移项、合并同类项,然后系数化成1即可求解.
解:(1)移项,得:2x<10﹣5,
合并同类项得:2x<5,
系数化成1得:x<;
(2)去分母,得:3(2+x)≥2(2x﹣1)﹣12,
去括号,得:6+3x≥4x﹣2﹣12,
移项,得:3x﹣4x≥﹣2﹣12﹣6,
合并同类项,得:﹣x≥﹣20,
系数化成1得:x≤20.
23.四边形ABCD中,AD=CD,AB=CB,连接AC、BD相交于点O.
(1)如图1,求证:DB平分∠ADC;
(2)如图2,若∠ADO=45°,∠OAB=60°,请直接写出四边形ABCD各内角的度数.
【分析】(1)根据SSS证明△ABD与△CBD全等,进而利用全等三角形的性质解答即可;
(2)根据四边形的内角解答即可.
【解答】证明:(1)在△ABD与△CBD中
,
∴△ABDD≌△CBD(SSS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
(2)∵∠ADO=45°,∠OAB=60°,
∴∠ADC=90°,∠DAB=∠ACB=105°,∠ABC=60°.
24.某中学对全校七年级学生进行了一次数学考试,随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的不完整的统计图.请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;并直接写出这部分学生成绩的中位数落在哪组?
(3)如果该学校七年级共有380人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀.
【分析】(1)“良”的有22人,占调查人数的44%,可求出调查人数,即全班的人数;
(2)计算出“中”的人数,找出成绩的中位数;
(3)样本估计总体,样本中成绩达到“优秀”的所占的百分比为(1﹣16%﹣20%﹣44%),进而求出相应的人数.
解:(1)22÷44%=50(人),
答:共调查50名学生;
(2)50﹣10﹣22﹣8=10(人),成绩从小到大排列后处在第25、26位的都是“良”,因此中位数是良;
(3)380×(1﹣16%﹣20%﹣44%)=76(人),
答:该校七年级共有76名学生的数学成绩可以达到优秀.
25.疫情爆发,物资紧缺,一医药集团主动担当作为,紧急投产口罩生产线,每天生产医用防护口罩或者医用外科口罩.已知2天生产医用防护口罩、1天生产医用外科口罩,可生产两种口罩共8万只;若1天生产医用防护口罩、3天生产医用外科口罩,可生产两种口罩共9万只.
(1)求平均每天生产医用防护口罩和医用外科口罩各多少万只?
(2)该集团现接到需要180万只口罩的订单,要求生产时间不能超过70天,则工厂至少能生产多少万只医用防护口罩?
【分析】(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,由题意可列出方程组,解方程组即可得出答案;
(2)设工厂至少能生产n万只医用防护口罩,列出不等式可得出答案.
解:(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,由题意得,
,
解得.
答:日平均生产医用防护口罩3万只,日平均生产医用外科口罩2万只.
(2)工厂生产n万只医用防护口罩,
∴.
解得n≥120,
∵n为正整数,
∴n的最小值为120.
答:工厂至少能生产120万只医用防护口罩.
26.已知:Rt△ABC中,∠CAB=90°,CA=BA,Rt△ADE中,∠DAE=90°,DA=EA,连接CE、BD.
(1)如图1,求证:CE=BD;
(2)如图2,当D在AC上,E在BA的延长线上,直线BD、CE相交于点F,求证:CE⊥BD;
(3)如图3,在(2)的条件下,若D是AC中点,BF=6,求△BEF的面积.
【分析】(1)由SAS证得△EAC≌△DAB,即可得出结论;
(2)由SAS证得△EAC≌△DAB,得出∠ECA=∠DBA,由三角形外角的性质得出∠CFD=∠BAD=90°,即可得出结论;
(3)连接AF,过点A作AP⊥CE于P、AQ⊥BF于Q,过点F作FR⊥BE于R,则∠APC=∠AQB=90°,由AAS证得△APC≌△AQB,得出AP=AQ,由S△AEF=AE?FR=EF?AP,S△ABF=AB?FR=BF?AQ,得出==,由D是AC中点,得出=,则===,求出EF的长,由S△BEF=BF?EF即可得出结果.
【解答】(1)证明:∵∠EAC=∠DAE+∠DAC=90°+∠DAC,∠DAB=∠CAB+∠DAC=90°+∠DAC,
∴∠EAC=∠DAB,
在△EAC和△DAB中,,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)证明:在△EAC和△DAB中,,
∴△EAC≌△DAB(SAS),
∴∠ECA=∠DBA,
∵∠CDB为△CFD、△ADB的外角,
∴∠CDB=∠ECA+∠CFD=∠DBA+∠BAD,
∴∠CFD=∠BAD=90°,
∴CE⊥BD;
(3)解:连接AF,过点A作AP⊥CE于P、AQ⊥BF于Q,过点F作FR⊥BE于R,如图3所示:
则∠APC=∠AQB=90°,
在△APC和△AQB中,,
∴△APC≌△AQB(AAS),
∴AP=AQ,
∵S△AEF=AE?FR=EF?AP,S△ABF=AB?FR=BF?AQ,
∴==,
∵D是AC中点,
∴=,
∵AD=AE,AC=AB,
∴===,
∴EF=BF=×6=3,
∵BF⊥EF,
∴S△BEF=BF?EF=×6×3=9.
27.如图,在平面直角坐标系中,点O为原点,A(0,a),B(b,0),已知a、b满足方程组.
(1)求A、B两点的坐标;
(2)点C从O出发,以每秒2个单位长度的速度沿y轴正半轴的方向运动,设点C的运动时间为t秒,连接BC,△ABC的面积为S,用含t的式子S表示(并直接写出t的取值范围);
(3)如图3,在(2)的条件下,当C点在OA上,S=30时,点E在CB的延长线上,连接AE,将线段AE绕点A逆时针旋转90°至线段AD,点D恰好在x轴的正半轴上,将线段BA绕点A逆时针旋转90°至线段FA,当点F在直线BC上时,求t值和点D的坐标.
【分析】(1)解方程组求出a,b的值,即可得出结论;
(2)分点C在线段OA和OA延长线上,表示出AC,最后,利用三角形的面积公式即可得出结论;
(3)先利用S=30,求出t的值,再判断出△ABO≌△FAG(AAS),得出FG=AO,AO=BO=6,进而判断出△AEH≌△DAO(AAS),得出EH=AO=12,AH=DO,∴EH=FG=AO=12,进而判断出△GCF≌△HCE(AAS),得出GC=CH,即可得出结论.
解:(1)∵,
∴,
∴A(0,12),B(﹣6,0);
(2)当点C在线段OA上时,即0≤t<6,CA=12﹣2t,
∵BO⊥OA,
∴S=CA?OB=(12﹣2t)×6=﹣6t+36;
当点C在OA的延长线上时,t>6,CA=2t﹣6,
∵BO⊥OA,
∴S=CA?OB=(2t﹣12)×6=6t﹣36,
即S=;
(3)如图,∵点C在线段OA上,S=30,
∴﹣6t+36=30,
∴t=1,
∴C(0,2),
过点F作FG⊥y轴于G,过点E作EH⊥y轴于H,
∴∠AGF=90°,
∴∠AFG+∠FAG=90°,
由旋转知,∠BAF=90°,
∴∠FAG+∠OAB=90°,
∴∠OAB=∠GFA,
由旋转知,AB=AF,∠AOB=∠FGA,
∴△ABO≌△FAG(AAS),
∴FG=AO,AO=BO=6,
∵∠AHE=90°,
∴∠HEA+∠EAH=90°,
由旋转知,AE=AD,∠EAD=90°,
∴∠EAH+∠DAO=90°,
∴∠HEA=∠DAO,
∵∠AOD=∠EHA,
∴△AEH≌△DAO(AAS),
∴EH=AO=12,AH=DO,
∴EH=FG=AO=12,
∵∠FGC=∠EHC=90°,∠ECH=∠GCF,
∴△GCF≌△HCE(AAS),
∴GC=CH,
∵GC=OA﹣OC﹣AG=12﹣2﹣6=4,
∴CH=CG=4,
∴OD=AH=10+4=14,
∴D(14,0).
一、选择题(共10小题).
1.下列方程是二元一次方程的是( )
A.2x﹣y=1
B.x2﹣2x+1=0
C.2x﹣1=0
D.x﹣3=2x
2.如果方程x=1与2x+a=ax的解相同,则a的值是( )
A.2
B.﹣2
C.3
D.﹣3
3.甲、乙两台机床生产一种零件,在10天中两台机床每天生产的次品数的平均数是==2,方差是:S甲2=1.65,S乙2=0.76,出次品的波动较小的机床是( )
A.甲机床
B.乙机床
C.甲、乙机床一样
D.不能确定
4.下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
5.为了预防新冠病毒,6名学生准备了口罩,口罩数量(单位:个)分别为:87、88、73、88、79、85,这组数据的众数是( )
A.79
B.87
C.88
D.85
6.不等式组的解集是( )
A.x≤﹣1
B.x≥3
C.﹣3≤x≤1
D.﹣3≤x<1
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm
B.5cm
C.6cm
D.7cm
8.△ABC中,它的三条角平分线的交点为O,若∠B=80°,则∠AOC的度数为( )
A.100°
B.130°
C.110°
D.150°
9.如图,△ADM中,AM=DM,∠AMD=90°,直线l经过点M,AB⊥l,DC⊥l,垂足分别为B,C,若AB=2,CD=5,则BC的长度为( )
A.1.5
B.3
C.4
D.5
10.下列说法中,正确的个数为( )
①三角形的外角等于两个内角的和;②有两边和一角分别相等的两个三角形全等;③各边都相等的多边形是正多边形;④到角两边距离相等的点,在这个角的平分线上.
A.1
B.2
C.3
D.0
二、填空题(每小题3分,共计30分)
11.把方程7x﹣y=15改写成用含x的式子表示y的形式为y=
.
12.“x的2倍与3的和不大于5”用不等式表示是
.
13.五边形的内角和为
度.
14.已知a、b满足方程组,则a+b的值为
.
15.若关于x的不等式(m﹣l)x<m﹣1的解集为x>1,则m的取值范围是
.
16.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中,要测量工件内槽宽AB,只要测
就可以了.
17.若一等腰三角形的两边长分别为3cm、7cm,则该三角形的周长为
.
18.如图,A,B分别是线段OC,OD上的点,OC=OD,OA=OB,若∠O=60°,∠C=25°,则∠BED的度数是
度.
19.在△ABC中,AD,AE分别是它的高线,角平分线,当∠B=40°,∠ACD=60°,则∠EAD的度数为
度.
20.如图,点A为∠MON的平分线上一点,过A任意作一条直线分别与∠MON的两边相交于B、C,P为BC中点,过P作BC的垂线交射线OA于点D,若∠MON=115°,则∠BDC的度数为
度.
三、解答题(其中21-24题各8分,25--26题各9分,27题10分,共计60分)
21.解下列方程组:
(1);
(2).
22.解下列不等式:
(1)2x+5<10;
(2)≥﹣2.
23.四边形ABCD中,AD=CD,AB=CB,连接AC、BD相交于点O.
(1)如图1,求证:DB平分∠ADC;
(2)如图2,若∠ADO=45°,∠OAB=60°,请直接写出四边形ABCD各内角的度数.
24.某中学对全校七年级学生进行了一次数学考试,随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的不完整的统计图.请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;并直接写出这部分学生成绩的中位数落在哪组?
(3)如果该学校七年级共有380人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀.
25.疫情爆发,物资紧缺,一医药集团主动担当作为,紧急投产口罩生产线,每天生产医用防护口罩或者医用外科口罩.已知2天生产医用防护口罩、1天生产医用外科口罩,可生产两种口罩共8万只;若1天生产医用防护口罩、3天生产医用外科口罩,可生产两种口罩共9万只.
(1)求平均每天生产医用防护口罩和医用外科口罩各多少万只?
(2)该集团现接到需要180万只口罩的订单,要求生产时间不能超过70天,则工厂至少能生产多少万只医用防护口罩?
26.已知:Rt△ABC中,∠CAB=90°,CA=BA,Rt△ADE中,∠DAE=90°,DA=EA,连接CE、BD.
(1)如图1,求证:CE=BD;
(2)如图2,当D在AC上,E在BA的延长线上,直线BD、CE相交于点F,求证:CE⊥BD;
(3)如图3,在(2)的条件下,若D是AC中点,BF=6,求△BEF的面积.
27.如图,在平面直角坐标系中,点O为原点,A(0,a),B(b,0),已知a、b满足方程组.
(1)求A、B两点的坐标;
(2)点C从O出发,以每秒2个单位长度的速度沿y轴正半轴的方向运动,设点C的运动时间为t秒,连接BC,△ABC的面积为S,用含t的式子S表示(并直接写出t的取值范围);
(3)如图3,在(2)的条件下,当C点在OA上,S=30时,点E在CB的延长线上,连接AE,将线段AE绕点A逆时针旋转90°至线段AD,点D恰好在x轴的正半轴上,将线段BA绕点A逆时针旋转90°至线段FA,当点F在直线BC上时,求t值和点D的坐标.
参考答案
一、选择题(每小题3分,共计30分)
1.下列方程是二元一次方程的是( )
A.2x﹣y=1
B.x2﹣2x+1=0
C.2x﹣1=0
D.x﹣3=2x
【分析】根据二元一次方程的定义逐个判断即可.
解:A、是二元一次方程,故本选项符合题意;
B、是一元二次方程,不是二元一次方程,故本选项不符合题意;
C、是一元一次方程,不是二元一次方程,故本选项不符合题意;
D、是一元一次方程,不是二元一次方程,故本选项不符合题意;
故选:A.
2.如果方程x=1与2x+a=ax的解相同,则a的值是( )
A.2
B.﹣2
C.3
D.﹣3
【分析】可以分别解出两方程的解,两解相等,就得到关于a的方程,从而可以求出a的值.
解:解第一个方程得:x=3,
解第二个方程得:x=
∴=3
解得:a=3
故选:C.
3.甲、乙两台机床生产一种零件,在10天中两台机床每天生产的次品数的平均数是==2,方差是:S甲2=1.65,S乙2=0.76,出次品的波动较小的机床是( )
A.甲机床
B.乙机床
C.甲、乙机床一样
D.不能确定
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解:∵S甲2=1.65,S乙2=0.76,
∴S甲2>S乙2,
∴出次品的波动较小的机床是乙机床;
故选:B.
4.下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
【分析】稳定性是三角形的特性.
解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
5.为了预防新冠病毒,6名学生准备了口罩,口罩数量(单位:个)分别为:87、88、73、88、79、85,这组数据的众数是( )
A.79
B.87
C.88
D.85
【分析】根据众数的概念求解可得.
解:这组数据的众数为88,
故选:C.
6.不等式组的解集是( )
A.x≤﹣1
B.x≥3
C.﹣3≤x≤1
D.﹣3≤x<1
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解:解不等式x+3≥0,得:x≥﹣3,
解不等式3x﹣1≤2,得:x≤1,
则不等式组的解集为﹣3≤x≤1.
故选:C.
7.如图,△ABC中,∠C=90°,E是AC上一点,连接BE,过E作DE⊥AB,垂足为D,BD=BC,若AC=6cm,则AE+DE的值为( )
A.4cm
B.5cm
C.6cm
D.7cm
【分析】根据全等三角形的性质求出DE=EC,求出AE+DE=AC,即可求出答案.
解:∵DE⊥AB于D,
∴∠BDE=90°,
在Rt△BDE和Rt△BCE中,
,
∴Rt△BDE≌Rt△BCE(HL),
∴ED=CE,
∴AE+ED=AE+CE=AC=6cm,
故选:C.
8.△ABC中,它的三条角平分线的交点为O,若∠B=80°,则∠AOC的度数为( )
A.100°
B.130°
C.110°
D.150°
【分析】先根据三角形的内角和定理求出∠BAC+∠BCA的度数,再根据角平分线的定义求出(∠BAC+∠BCA),然后再利用三角形的内角和定理求解即可.
解:∵AO,CO分别是∠BAC,∠BCA的平分线,
∴∠OAC=∠BAC,∠OCA=∠BCA,
∴∠AOC=180°﹣∠OAC﹣∠OCA
=180°﹣∠BAC﹣∠BCA,
=180°﹣(∠BAC+∠BCA).
又∵∠B=80°,
∴∠BAC+∠BCA=180°﹣80°=100°.
∴(∠BAC+∠BCA)=100°×=50°.
∴∠AOC=180°﹣50°=130°,
故选:B.
9.如图,△ADM中,AM=DM,∠AMD=90°,直线l经过点M,AB⊥l,DC⊥l,垂足分别为B,C,若AB=2,CD=5,则BC的长度为( )
A.1.5
B.3
C.4
D.5
【分析】根据全等三角形的判定和性质得出AB=CM,CD=BM,进而解答即可.
解:∵AB⊥l,DC⊥l,
∴∠DCM=∠MBA=90°,∠MDC+∠DMC=90°,
∵∠AMD=90°,
∴∠DMC+∠AMB=90°,
∴∠MDC=∠AMB,
在△DMC与△MAB中
,
∴△DMC≌△MAB(AAS),
∴AB=CM=2,CD=BM=5,
∴BC=BM﹣CM=5﹣2=3,
故选:B.
10.下列说法中,正确的个数为( )
①三角形的外角等于两个内角的和;②有两边和一角分别相等的两个三角形全等;③各边都相等的多边形是正多边形;④到角两边距离相等的点,在这个角的平分线上.
A.1
B.2
C.3
D.0
【分析】根据三角形的外角的性质,全等三角形的判定,正多边形的定义,角平分线的判定定理一一判断即可.
解:①三角形的外角等于两个内角的和,错误,应该是三角形的外角等于和它不相邻两个内角的和.
②有两边和一角分别相等的两个三角形全等,错误,应该是有两边和夹角分别相等的两个三角形全等.
③各边都相等的多边形是正多边形,错误.缺少各个角相等这个条件.
④到角两边距离相等的点,在这个角的平分线上.错误,这个点必须在这个角的内部.
故选:D.
二、填空题(每小题3分,共计30分)
11.把方程7x﹣y=15改写成用含x的式子表示y的形式为y= 7x﹣15 .
【分析】将x看做已知数求出y即可.
解:∵7x﹣y=15,
∴y=7x﹣15,
故答案为:7x﹣15.
12.“x的2倍与3的和不大于5”用不等式表示是 2x+3≤5 .
【分析】首先表示“x的2倍”为2x,再表示“与3的和”为2x+3,最后表示“不大于5”可得2x+3≤5.
解:由题意得:2x+3≤5,
故答案为2x+3≤5.
13.五边形的内角和为 540 度.
【分析】n边形内角和公式为(n﹣2)180°,把n=5代入可求五边形内角和.
解:五边形的内角和为(5﹣2)×180°=540°.
故答案为:540.
14.已知a、b满足方程组,则a+b的值为 5 .
【分析】求出方程组的解得到a与b的值,即可确定出a+b的值.
解:,
①+②得:4a+4b=20,
即4(a+b)=20,
解得a+b=5.
故答案为:5.
15.若关于x的不等式(m﹣l)x<m﹣1的解集为x>1,则m的取值范围是 m<1 .
【分析】根据不等式的基本性质3,两边都除以m﹣1后得到x>1,可知m﹣1<0,解之可得.
解:∵将不等式(m﹣1)x<m﹣1两边都除以(m﹣1),得x>1,
∴m﹣1<0,
解得:m<1,
故答案为m<1.
16.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中,要测量工件内槽宽AB,只要测 A'B' 就可以了.
【分析】让我们了解测量两点之间的距离,只要符合全等三角形全等的条件之一SAS,只需要测量易测量的边A'B'上.测量方案的操作性强.
解:答:只要测量A'B'.
理由:连接AB,A'B',如图,
∵点O分别是AC、BB'的中点,
∴OA=OA',OB=OB'.
在△AOB和△A'OB'中,
OA=OA',∠AOB=∠A'OB'(对顶角相等),OB=OB',
∴△AOB≌△A'OB'(SAS).
∴A'B'=AB.
答:需要测量A'B'的长度,即为工件内槽宽AB,
故答案为:A'B'
17.若一等腰三角形的两边长分别为3cm、7cm,则该三角形的周长为 17cm .
【分析】题中没有指出哪个底哪个是腰,故应该分情况进行分析,注意应用三角形三边关系进行验证能否组成三角形.
解:当3cm是腰时,3+3<7,不符合三角形三边关系,故舍去;
当7cm是腰时,周长=7+7+3=17cm.
故它的周长为17cm.
故答案为:17cm.
18.如图,A,B分别是线段OC,OD上的点,OC=OD,OA=OB,若∠O=60°,∠C=25°,则∠BED的度数是 70 度.
【分析】证△ODA≌△OCB,推出∠D=∠C=25°,根据三角形外角性质求出∠DBE,根据三角形内角和定理求出即可.
解:在△ODA和△OCB中
,
∴△ODA≌△OCB(SAS),
∴∠D=∠C=25°,
∵∠O=60°,∠C=25°,
∴∠DBE=60°+25°=85°,
∴∠BED=180°﹣85°﹣25°=70°,
故答案为:70.
19.在△ABC中,AD,AE分别是它的高线,角平分线,当∠B=40°,∠ACD=60°,则∠EAD的度数为 10或40 度.
【分析】由三角形内角和可求得∠BAC,则由角平分线的定义可求得∠BAE,在Rt△BAD中,可求得∠BAD,则可求得∠EAD.
解:当高AD在△ABC的内部时.
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣40°﹣60°=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°,
∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=90°﹣∠B=50°,
∴∠EAD=∠BAD﹣∠BAE=50°﹣40°=10°.
当高AD在△ABC的外部时.
同法可得∠EAD=10°+30°=40°
故答案为10或40.
20.如图,点A为∠MON的平分线上一点,过A任意作一条直线分别与∠MON的两边相交于B、C,P为BC中点,过P作BC的垂线交射线OA于点D,若∠MON=115°,则∠BDC的度数为 65 度.
【分析】过D作DE⊥OM于E,DF⊥ON于F,求出∠EDF,根据角平分线性质求出DE=DF,根据线段垂直平分线性质求出BD=CD,证Rt△DEB≌Rt△DFC,求出∠EDB=∠CDF,推出∠BDC=∠EDF,即可得出答案.
解:如图:过D作DE⊥OM于E,DF⊥ON于F,
则∠DEB=∠DFC=∠DFO=90°,
∵∠MON=115°,
∴∠EDF=360°﹣90°﹣90°﹣115°=65°,
∵DE⊥OM,DF⊥ON,OD∠MON,
∴DE=DF,
∵P为BC中点,DP⊥BC,
∴BD=CD,
在Rt△DEB和Rt△DFC中,,
∴Rt△DEB≌Rt△DFC(HL),
∴∠EDB=∠CDF,
∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=65°.
故答案为:65.
三、解答题(其中21-24题各8分,25--26题各9分,27题10分,共计60分)
21.解下列方程组:
(1);
(2).
【分析】(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解:(1),
把②代入①得:6y﹣7﹣y=13,
解得:y=4,
把y=4代入①得:x=17,
则方程组的解为;
(2),
①+②得:4n=12,
解得:n=3,
把n=3代入①得:m=3,
则方程组的解为.
22.解下列不等式:
(1)2x+5<10;
(2)≥﹣2.
【分析】(1)移项、合并同类项,然后系数化成1即可求解;
(2)去分母、去括号、移项、合并同类项,然后系数化成1即可求解.
解:(1)移项,得:2x<10﹣5,
合并同类项得:2x<5,
系数化成1得:x<;
(2)去分母,得:3(2+x)≥2(2x﹣1)﹣12,
去括号,得:6+3x≥4x﹣2﹣12,
移项,得:3x﹣4x≥﹣2﹣12﹣6,
合并同类项,得:﹣x≥﹣20,
系数化成1得:x≤20.
23.四边形ABCD中,AD=CD,AB=CB,连接AC、BD相交于点O.
(1)如图1,求证:DB平分∠ADC;
(2)如图2,若∠ADO=45°,∠OAB=60°,请直接写出四边形ABCD各内角的度数.
【分析】(1)根据SSS证明△ABD与△CBD全等,进而利用全等三角形的性质解答即可;
(2)根据四边形的内角解答即可.
【解答】证明:(1)在△ABD与△CBD中
,
∴△ABDD≌△CBD(SSS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
(2)∵∠ADO=45°,∠OAB=60°,
∴∠ADC=90°,∠DAB=∠ACB=105°,∠ABC=60°.
24.某中学对全校七年级学生进行了一次数学考试,随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的不完整的统计图.请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;并直接写出这部分学生成绩的中位数落在哪组?
(3)如果该学校七年级共有380人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀.
【分析】(1)“良”的有22人,占调查人数的44%,可求出调查人数,即全班的人数;
(2)计算出“中”的人数,找出成绩的中位数;
(3)样本估计总体,样本中成绩达到“优秀”的所占的百分比为(1﹣16%﹣20%﹣44%),进而求出相应的人数.
解:(1)22÷44%=50(人),
答:共调查50名学生;
(2)50﹣10﹣22﹣8=10(人),成绩从小到大排列后处在第25、26位的都是“良”,因此中位数是良;
(3)380×(1﹣16%﹣20%﹣44%)=76(人),
答:该校七年级共有76名学生的数学成绩可以达到优秀.
25.疫情爆发,物资紧缺,一医药集团主动担当作为,紧急投产口罩生产线,每天生产医用防护口罩或者医用外科口罩.已知2天生产医用防护口罩、1天生产医用外科口罩,可生产两种口罩共8万只;若1天生产医用防护口罩、3天生产医用外科口罩,可生产两种口罩共9万只.
(1)求平均每天生产医用防护口罩和医用外科口罩各多少万只?
(2)该集团现接到需要180万只口罩的订单,要求生产时间不能超过70天,则工厂至少能生产多少万只医用防护口罩?
【分析】(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,由题意可列出方程组,解方程组即可得出答案;
(2)设工厂至少能生产n万只医用防护口罩,列出不等式可得出答案.
解:(1)设日平均生产医用防护口罩x万只,日平均生产医用外科口罩y万只,由题意得,
,
解得.
答:日平均生产医用防护口罩3万只,日平均生产医用外科口罩2万只.
(2)工厂生产n万只医用防护口罩,
∴.
解得n≥120,
∵n为正整数,
∴n的最小值为120.
答:工厂至少能生产120万只医用防护口罩.
26.已知:Rt△ABC中,∠CAB=90°,CA=BA,Rt△ADE中,∠DAE=90°,DA=EA,连接CE、BD.
(1)如图1,求证:CE=BD;
(2)如图2,当D在AC上,E在BA的延长线上,直线BD、CE相交于点F,求证:CE⊥BD;
(3)如图3,在(2)的条件下,若D是AC中点,BF=6,求△BEF的面积.
【分析】(1)由SAS证得△EAC≌△DAB,即可得出结论;
(2)由SAS证得△EAC≌△DAB,得出∠ECA=∠DBA,由三角形外角的性质得出∠CFD=∠BAD=90°,即可得出结论;
(3)连接AF,过点A作AP⊥CE于P、AQ⊥BF于Q,过点F作FR⊥BE于R,则∠APC=∠AQB=90°,由AAS证得△APC≌△AQB,得出AP=AQ,由S△AEF=AE?FR=EF?AP,S△ABF=AB?FR=BF?AQ,得出==,由D是AC中点,得出=,则===,求出EF的长,由S△BEF=BF?EF即可得出结果.
【解答】(1)证明:∵∠EAC=∠DAE+∠DAC=90°+∠DAC,∠DAB=∠CAB+∠DAC=90°+∠DAC,
∴∠EAC=∠DAB,
在△EAC和△DAB中,,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)证明:在△EAC和△DAB中,,
∴△EAC≌△DAB(SAS),
∴∠ECA=∠DBA,
∵∠CDB为△CFD、△ADB的外角,
∴∠CDB=∠ECA+∠CFD=∠DBA+∠BAD,
∴∠CFD=∠BAD=90°,
∴CE⊥BD;
(3)解:连接AF,过点A作AP⊥CE于P、AQ⊥BF于Q,过点F作FR⊥BE于R,如图3所示:
则∠APC=∠AQB=90°,
在△APC和△AQB中,,
∴△APC≌△AQB(AAS),
∴AP=AQ,
∵S△AEF=AE?FR=EF?AP,S△ABF=AB?FR=BF?AQ,
∴==,
∵D是AC中点,
∴=,
∵AD=AE,AC=AB,
∴===,
∴EF=BF=×6=3,
∵BF⊥EF,
∴S△BEF=BF?EF=×6×3=9.
27.如图,在平面直角坐标系中,点O为原点,A(0,a),B(b,0),已知a、b满足方程组.
(1)求A、B两点的坐标;
(2)点C从O出发,以每秒2个单位长度的速度沿y轴正半轴的方向运动,设点C的运动时间为t秒,连接BC,△ABC的面积为S,用含t的式子S表示(并直接写出t的取值范围);
(3)如图3,在(2)的条件下,当C点在OA上,S=30时,点E在CB的延长线上,连接AE,将线段AE绕点A逆时针旋转90°至线段AD,点D恰好在x轴的正半轴上,将线段BA绕点A逆时针旋转90°至线段FA,当点F在直线BC上时,求t值和点D的坐标.
【分析】(1)解方程组求出a,b的值,即可得出结论;
(2)分点C在线段OA和OA延长线上,表示出AC,最后,利用三角形的面积公式即可得出结论;
(3)先利用S=30,求出t的值,再判断出△ABO≌△FAG(AAS),得出FG=AO,AO=BO=6,进而判断出△AEH≌△DAO(AAS),得出EH=AO=12,AH=DO,∴EH=FG=AO=12,进而判断出△GCF≌△HCE(AAS),得出GC=CH,即可得出结论.
解:(1)∵,
∴,
∴A(0,12),B(﹣6,0);
(2)当点C在线段OA上时,即0≤t<6,CA=12﹣2t,
∵BO⊥OA,
∴S=CA?OB=(12﹣2t)×6=﹣6t+36;
当点C在OA的延长线上时,t>6,CA=2t﹣6,
∵BO⊥OA,
∴S=CA?OB=(2t﹣12)×6=6t﹣36,
即S=;
(3)如图,∵点C在线段OA上,S=30,
∴﹣6t+36=30,
∴t=1,
∴C(0,2),
过点F作FG⊥y轴于G,过点E作EH⊥y轴于H,
∴∠AGF=90°,
∴∠AFG+∠FAG=90°,
由旋转知,∠BAF=90°,
∴∠FAG+∠OAB=90°,
∴∠OAB=∠GFA,
由旋转知,AB=AF,∠AOB=∠FGA,
∴△ABO≌△FAG(AAS),
∴FG=AO,AO=BO=6,
∵∠AHE=90°,
∴∠HEA+∠EAH=90°,
由旋转知,AE=AD,∠EAD=90°,
∴∠EAH+∠DAO=90°,
∴∠HEA=∠DAO,
∵∠AOD=∠EHA,
∴△AEH≌△DAO(AAS),
∴EH=AO=12,AH=DO,
∴EH=FG=AO=12,
∵∠FGC=∠EHC=90°,∠ECH=∠GCF,
∴△GCF≌△HCE(AAS),
∴GC=CH,
∵GC=OA﹣OC﹣AG=12﹣2﹣6=4,
∴CH=CG=4,
∴OD=AH=10+4=14,
∴D(14,0).
同课章节目录
