11.2.1三角形的内角(2)课件(共18张PPT)
文档属性
| 名称 | 11.2.1三角形的内角(2)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
人教版
八年级数学上
11.2.1
三角形的内角(2)
学习目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
情境导入
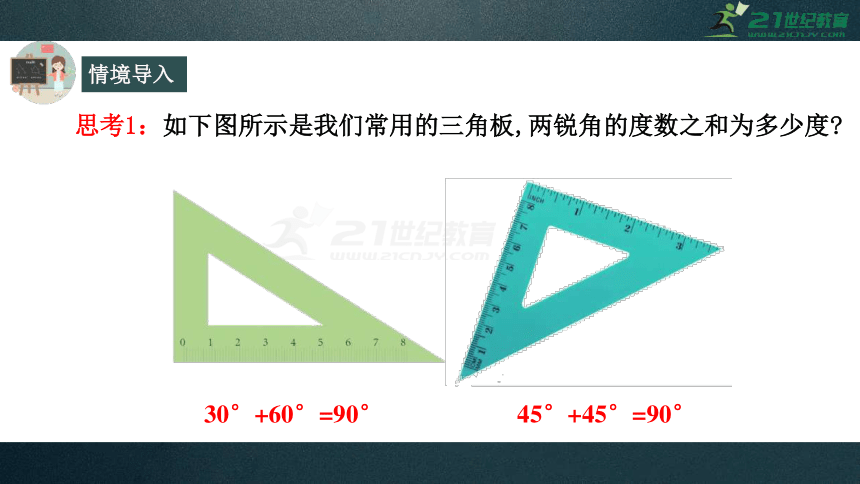
思考1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度?
30°+60°=90°
45°+45°=90°
合作探究
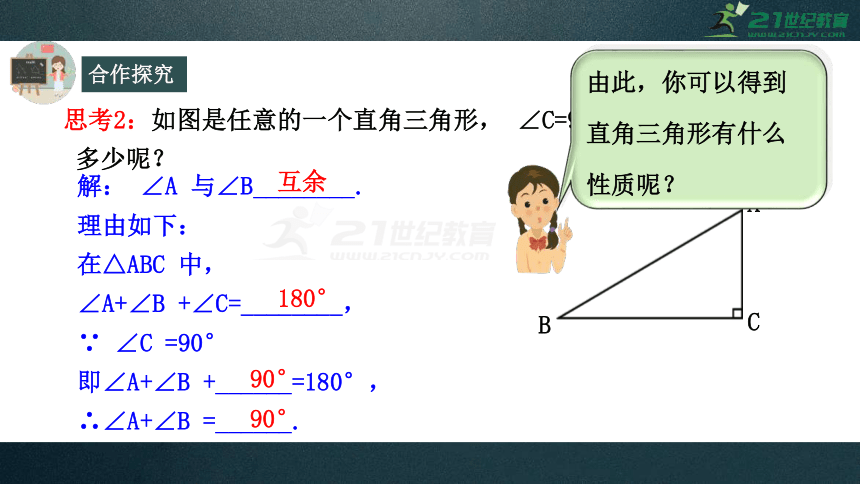
思考2:如图是任意的一个直角三角形,
∠C=90°,两锐角的和等于
多少呢?
A
B
C
解:
∠A
与∠B________.
理由如下:
在△ABC
中,
∠A+∠B
+∠C=________,
∵
∠C
=90°
即∠A+∠B
+______=180°,
∴∠A+∠B
=______.
互余
180°
90°
90°
由此,你可以得到直角三角形有什么性质呢?
合作探究
A
B
C
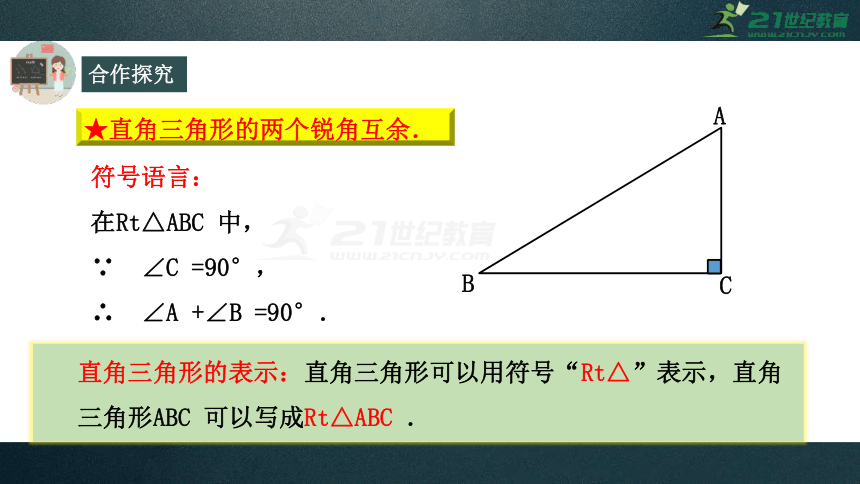
★直角三角形的两个锐角互余.
符号语言:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角
三角形ABC
可以写成Rt△ABC
.
小试牛刀
1.在一个直角三角形中,有一个锐角等于15°,则另一个锐角的度数是(
)
A.30°
B.45°
C.60°
D.75°
2.下列条件中不能使△ABC成为直角三角形的是(
)
A.∠A+∠B=∠C
B.∠A=∠B=
∠C
C.∠A∶∠B∶∠C=2∶3∶5
D.∠A=2∠B=3∠C
D
D
小试牛刀
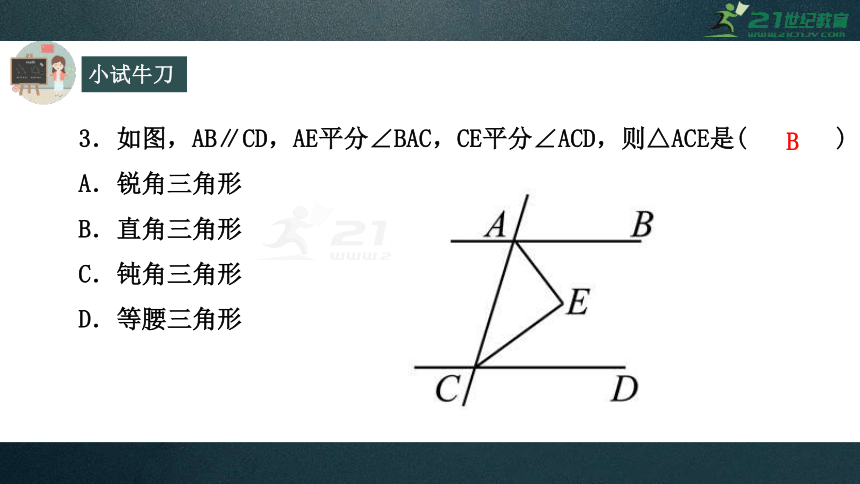
3.如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,则△ACE是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
B
合作探究
思考3:反过来,有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC是直角三角形吗?
在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
由此,你可以得到直角三角形有什么判定呢?
合作探究
符号语言:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
★有两个角互余的三角形是直角三角形.
A
B
C
小试牛刀
1、如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
小试牛刀
2.如图,在△ABC中,AD⊥BC于点D,∠1=∠B.
试说明:△ABC是
直角三角形.
解:∵AD⊥BC,
∴∠1+∠C=90°,
又∵∠1=∠B,
∴∠B+∠C=90°,
∴△ABC是直角三角形
综合演练
2.如图,AD是Rt
△ABC的斜边BC上的高,则图中与∠B互
余的角有(
)
A.1个
B.2个
C.3个
D.4个
1.如图,AB,CD相交于点O,AC⊥CD于点C.
若∠BOD=38°,则∠A=
.
B
52°
综合演练
3.如图,∠C
=∠D
=90°,AD,BC
相交于点E,∠CAE
与∠DBE
有什么关系?为什么?
解:相等.理由如下,
在Rt
△ACE中
∠CAE
=90°-∠AEC
在Rt
△BDE
中,
∠DBE=90°-∠BED
∵∠AEC
=∠BED
∴∠CAE
=∠DBE
综合演练
4.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
解:(1)∠1=∠2.
理由:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE是直角三角形,
∴∠1+∠B=90°,∠2+∠B=90°,
∴∠1=∠2
(1)猜想∠1与∠2的关系,并说明理由;
综合演练
解:
(2)结论仍然成立.理由:
∵AD⊥BC,CE⊥AB,
∴∠D=∠E=90°,
∴∠1+∠CBE=90°,∠2+∠DBA=90°.
∵∠DBA=∠CBE,
∴∠1=∠2
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?说明理由.
2.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
课堂小结
今天我们收获了哪些知识?
1.说一说直角三角形的性质及判定?
2.利用直角三角形的性质与判定分别可以解决哪些问题?
课后作业
教材16页习题11.2第4、10题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
11.2.1
三角形的内角(2)
学习目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
情境导入
思考1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度?
30°+60°=90°
45°+45°=90°
合作探究
思考2:如图是任意的一个直角三角形,
∠C=90°,两锐角的和等于
多少呢?
A
B
C
解:
∠A
与∠B________.
理由如下:
在△ABC
中,
∠A+∠B
+∠C=________,
∵
∠C
=90°
即∠A+∠B
+______=180°,
∴∠A+∠B
=______.
互余
180°
90°
90°
由此,你可以得到直角三角形有什么性质呢?
合作探究
A
B
C
★直角三角形的两个锐角互余.
符号语言:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角
三角形ABC
可以写成Rt△ABC
.
小试牛刀
1.在一个直角三角形中,有一个锐角等于15°,则另一个锐角的度数是(
)
A.30°
B.45°
C.60°
D.75°
2.下列条件中不能使△ABC成为直角三角形的是(
)
A.∠A+∠B=∠C
B.∠A=∠B=
∠C
C.∠A∶∠B∶∠C=2∶3∶5
D.∠A=2∠B=3∠C
D
D
小试牛刀
3.如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,则△ACE是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
B
合作探究
思考3:反过来,有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC是直角三角形吗?
在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
由此,你可以得到直角三角形有什么判定呢?
合作探究
符号语言:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
★有两个角互余的三角形是直角三角形.
A
B
C
小试牛刀
1、如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
小试牛刀
2.如图,在△ABC中,AD⊥BC于点D,∠1=∠B.
试说明:△ABC是
直角三角形.
解:∵AD⊥BC,
∴∠1+∠C=90°,
又∵∠1=∠B,
∴∠B+∠C=90°,
∴△ABC是直角三角形
综合演练
2.如图,AD是Rt
△ABC的斜边BC上的高,则图中与∠B互
余的角有(
)
A.1个
B.2个
C.3个
D.4个
1.如图,AB,CD相交于点O,AC⊥CD于点C.
若∠BOD=38°,则∠A=
.
B
52°
综合演练
3.如图,∠C
=∠D
=90°,AD,BC
相交于点E,∠CAE
与∠DBE
有什么关系?为什么?
解:相等.理由如下,
在Rt
△ACE中
∠CAE
=90°-∠AEC
在Rt
△BDE
中,
∠DBE=90°-∠BED
∵∠AEC
=∠BED
∴∠CAE
=∠DBE
综合演练
4.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
解:(1)∠1=∠2.
理由:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE是直角三角形,
∴∠1+∠B=90°,∠2+∠B=90°,
∴∠1=∠2
(1)猜想∠1与∠2的关系,并说明理由;
综合演练
解:
(2)结论仍然成立.理由:
∵AD⊥BC,CE⊥AB,
∴∠D=∠E=90°,
∴∠1+∠CBE=90°,∠2+∠DBA=90°.
∵∠DBA=∠CBE,
∴∠1=∠2
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?说明理由.
2.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
课堂小结
今天我们收获了哪些知识?
1.说一说直角三角形的性质及判定?
2.利用直角三角形的性质与判定分别可以解决哪些问题?
课后作业
教材16页习题11.2第4、10题.
https://www.21cnjy.com/help/help_extract.php
