济南济北中学2019-2020学年鲁科版选修3-4:1.3单摆 配套作业(含解析)
文档属性
| 名称 | 济南济北中学2019-2020学年鲁科版选修3-4:1.3单摆 配套作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-06 10:11:11 | ||
图片预览




文档简介
1.3单摆
1.2013年6月,我国宇航员在天宫一号空间站中进行我国首次太空授课活动,展示了许多在地面上无法实现的实验现象.假如要在空间站再次进行授课活动,下列我们曾在实验室中进行的实验,若移到空间站也能够实现操作的有(
)
A.利用托盘天平测质量
B.利用弹簧测力计测拉力
C.利用自由落体验证机械能守恒定律
D.测定单摆做简谐运动的周期
2.一物体在某行星表面受到的万有引力是它在地球表面受到的万有引力的.在地球上走得很准的摆钟搬到此行星上后,此钟的分针走一整圈所经历的实际时间是( )
A.
B.
C.2h
D.4h
3.关于单摆,下列说法中正确的是( )
A.单摆摆球所受的合外力指向平衡位置
B.摆球经过平衡位置时加速度为零
C.摆球运动到平衡位置时,所受回复力等于零
D.摆角很小时,摆球所受合力的大小跟摆球相对平衡位置的位移大小成正比
4.如图所示,光滑圆弧槽半径为
R,
A
为圆弧的最低点,圆弧的最高点到
A
的距离远小于
R。两个可视为质点的小球B
和C
都由静止开始释放。设点
B
到点
A
的距离为
H,则以下所给的四
个H
值中,可以使
B、C
两球在点A
相遇的是(
)
A.
B.
C.
D.
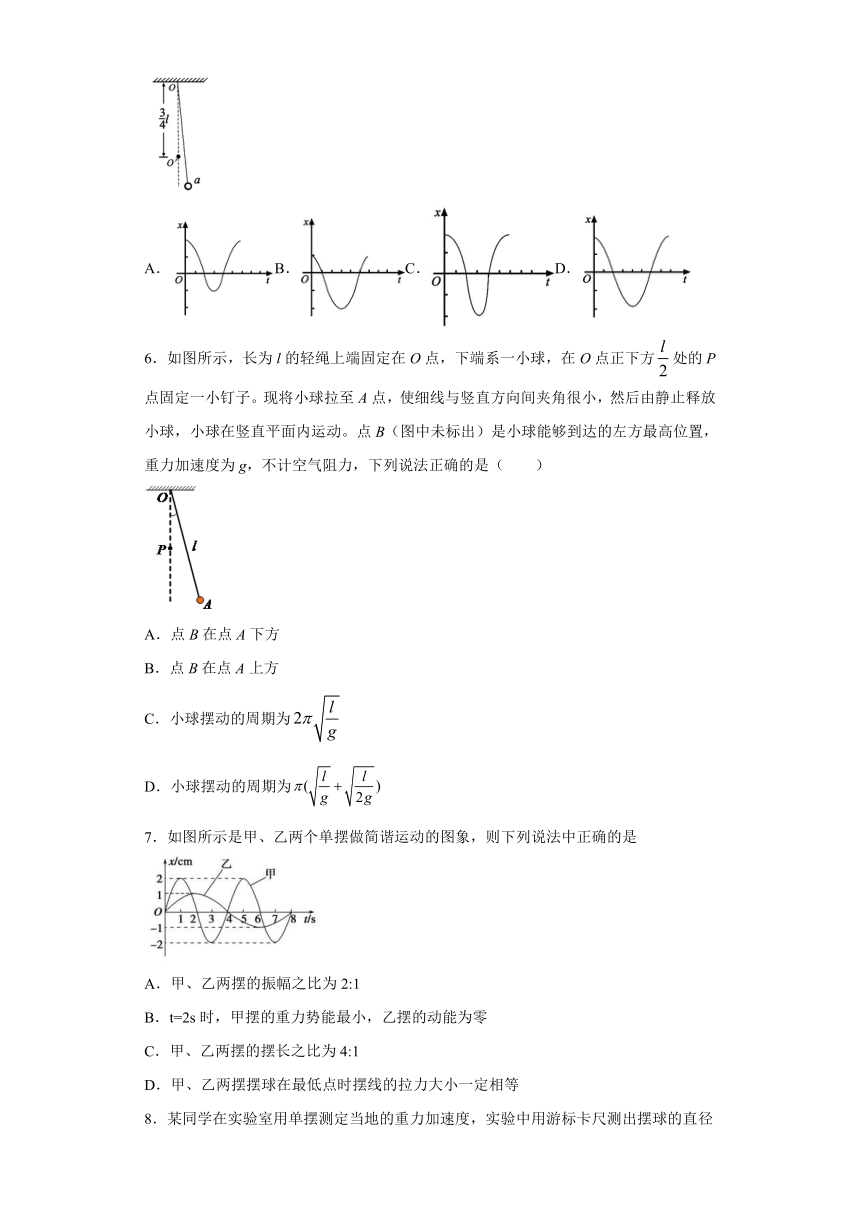
5.如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A.B.C.D.
6.如图所示,长为l的轻绳上端固定在O点,下端系一小球,在O点正下方处的P点固定一小钉子。现将小球拉至A点,使细线与竖直方向间夹角很小,然后由静止释放小球,小球在竖直平面内运动。点B(图中未标出)是小球能够到达的左方最高位置,重力加速度为g,不计空气阻力,下列说法正确的是( )
A.点B在点A下方
B.点B在点A上方
C.小球摆动的周期为
D.小球摆动的周期为
7.如图所示是甲、乙两个单摆做简谐运动的图象,则下列说法中正确的是
A.甲、乙两摆的振幅之比为2:1
B.t=2s时,甲摆的重力势能最小,乙摆的动能为零
C.甲、乙两摆的摆长之比为4:1
D.甲、乙两摆摆球在最低点时摆线的拉力大小一定相等
8.某同学在实验室用单摆测定当地的重力加速度,实验中用游标卡尺测出摆球的直径d,再用米尺测出从悬点至小球上端的悬线长l0;让单摆在竖直平面内做小角度摆动,摆球第一次通过最低点时开始计时,当摆球第N次通过最低点时停止计时,测得时间为t;利用单摆的周期公式计算重力加速度g,变更摆长重做几次,得到g的平均值。该同学发现g的平均值比当地公布的重力加速度的值略大,其原因可能是__。
A.计算摆长时,取l=l0+d
B.计算摆长时,取l=l0
C.计算周期时,取T=
D.实验中,摆线上端未牢固地系于悬点,振动中出现松动
E.实验室地下有重金属矿物质
9.在用单摆测定重力加速度的实验中,下列措施中必要的或做法正确的是______;
A.为了便于计时观察,单摆的摆角应尽量大些
B.摆线长应远远大于摆球直径
C.摆球应选择密度较大的实心金属小球
D.用停表测量周期时,应测量单摆30~50次全振动的时间,然后计算周期,而不能把只测一次全振动时间当作周期
E.将摆球和摆线平放在桌面上,拉直后用米尺测出摆球球心到摆线某点O间的长度作为摆长,然后将O点作为悬点
10.如图所示,用绝缘细线悬挂的单摆,摆球带正电,悬挂于O点,摆长为l,当它摆过竖直线OC时便进入或离开匀强磁场,磁场方向垂直于单摆摆动的平面向里,A,B点分别是最大位移处.下列说法中正确的是( )
A.A点和B点处于同一水平面
B.A点高于B点
C.摆球在A点和B点处线上的拉力大小相等
D.单摆的振动周期仍为
E.单摆向右或向左摆过D点时,线上的拉力大小相等
11.如图,房顶上固定一根长2.5m的细线沿竖直墙壁垂到窗沿下,细线下端系了一个小球(可视为质点)。打开窗子,让小球在垂直于窗子的竖直平面内小幅摆动,窗上沿到房顶的高度为1.6m,不计空气阻力,g取10m/s2,则小球在摆动过程中的回复力是由__________提供的,从最左端运动到最右端的最短时间为________________s。
12.在向下匀速直线运动的升降机中有一摆长为L的单摆在做简谐振动,当该升降机以加速度a(g为重力加速度)竖直下降时,摆的振动周期为_______________。若在单摆摆到最低点时,升降机突然做自由落体运动,则摆球相对升降机做______________。若在单摆摆到最高点时,升降机突然做自由落体运动,则摆球相对升降机做_____________
;(升降机内部空气阻力不计,
且最后两空均用文字说明运动情况)
13.如图甲所示,一个单摆做小角度摆动。从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图像如图乙所示。不计空气阻力,取。对于这个单摆的振动过程,单摆的位移x随时间t变化的关系式为________cm,单摆的摆长为________m,从t=2.5s到t=3.0s的过程中,摆球所受回复力逐渐________(填“增大”或“减小”)。
14.单摆是一种理想模型,能看做单摆的条件是:摆线不可伸长,摆线质量远______摆球质量,摆线长度远_____________摆球直径(均填“大于”或“小于”)。单摆的摆角小于5°时,可看做简谐运动,此时周期公式是__________。如图所示,在一半径为2.5m的光滑圆轨道上切下一段圆弧,放置于竖直平面内,将一个小钢珠置于圆轨道最低点附近并从静止释放。有同学说,这个小钢珠运动到最低点的最短时间可以用单摆的周期公式去求,他说的有道理吗?请判断并分析说明。______________________
参考答案
1.B
【解析】
天宫一号空间站围绕地球做匀速圆周运动,所受到的万有引力充当了向心力,天宫一号空间站中的物体均处在完全失重状态,所以靠重力作用的实验均不能成功,故只有B选项正确。
故选B.
2.C
【解析】
根据在星球表面万有引力等于重力可知:某行星表面受到的万有引力是它在地球表面受到的万有引力的,质量不变,所以该星球的重力加速度
根据公式
拿到某行星上周期,分针走一圈的时间为地球上的2倍,故C正确,ABD错误。
3.C
【解析】
A.根据回复力的特点可知摆球受到的回复力方向总是指向平衡位置,但合力并不总是指向平衡位置,故A错误;
B.摆球经过平衡位置时,由于做圆周运动,故存在向心加速度,故B错误;
C.摆球运动到平衡位置时,回复力等于零,故C正确;
D.摆角很小时,摆球所受回复力的大小跟摆球对平衡位置的位移大小成正比,而不是合力的大小跟摆球对平衡位置的位移大小成正比,故D错误。
故选C。
4.D
【解析】
对B球,有
解得
对C球,周期为
所以有
由于t=t′,故
解得
(其中:n=0、1、2、3…)
当n=0时,可得
当n=1时,可得
由此可知D符合题意,ABC不符合题意。
5.A
【解析】
由T=2π得:T1=2π,T2=2π=π=T1
,故BD错误;
,
由能量守恒定律可知,小球先后摆起得最大高度相同,故l-lcosθ1=
根据数学规律可得:
故,即第一次振幅是第二次振幅得2倍,故A正确,C错误.
6.D
【解析】
AB.小球摆动过程中,只有重力做功,机械能守恒,可知两侧最高点动能均为零,故重力势能也相等,故最大高度相同,即点B与点A等高,故AB错误;
CD.小球从最低点到A点再到最低点的时间为
小球从最低点到B点再到最低点的时间为
则小球的周期为
故C错误,D正确。
故选D。
7.AB
【解析】
由图知甲、乙两摆的振幅分别为2?cm、1?cm,故选项A正确;t=2?s时,甲摆在平衡位置处重力势能最小;乙摆在振动的最大位移处,动能为零,故选项B正确;甲、乙两摆的周期之比为1:2,由单摆的周期公式T=2π,得到甲、乙两摆的摆长之比为1:4,故选项C错误;由题目的条件不能比较甲、乙两摆摆球在最低点时摆线的拉力大小,故选项D错误;故选AB。
8.ACE
【解析】
由单摆的周期公式可得
A.计算摆长时,取l=l0+d,则摆长测量值偏大,由可知,重力加速度测量值偏大,故A正确;
B.计算摆长时,取l=l0时,则摆长测值偏小,由可知,重力加速度测量值偏小,故B错误;
C.计算周期时,取T=则周期偏小,由可知,重力加速度测量值偏大,故C正确;
D.实验中,摆线上端未牢固地系于悬点,振动中出现松动,则摆长测量值偏小,由可知,重力加速度测量值偏小,故D错误;
E.实验室地下有重金属矿物质,小球受到地球的引力增大,则重力加速度偏大,故E正确。
故选ACE。
9.BCD
【解析】
A.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过5°,否则单摆将不做简谐运动,故A错误;
BC.为了减小空气阻力的影响,摆球的直径应远小于摆线的长度,并选择密度较大的实心金属小球作为摆球,故BC正确;
D.为了减小测量误差,应采用累积法测量周期,即测量单摆30~50次全振动的时间t,再求出周期T,故D正确;
E.这样做很难保证悬点就是O点,就会导致摆长测量不准确,应将单摆悬点固定后,用米尺测出摆球球心到悬点的距离作为摆长,所以E错误。
故选BCD。
10.ACD
【解析】
摆球运动过程中机械能守恒,所以A,B在同一高度.选项A正确,B错误;球在B点不受洛伦兹力,与球在A点时受拉力大小相等,选项C正确;球在磁场中运动时虽然受洛伦兹力,但洛伦兹力总与速度方向垂直,不能提供回复力,所以不改变振动的周期,选项D正确;单摆向右或向左摆过D点时,速度大小相等,但洛伦兹力的方向相反,所以线上的拉力不相等,选项E错误.
【点睛】本题中小球在复合场运动,洛伦兹力不做功,其机械能仍然守恒,洛伦兹力不改变小球运动的快慢.但要注意洛伦兹力方向与速度有关,速度反向,洛伦兹力方向也相反.
11.重力沿切线方向的分力(或重力沿运动方向的分力)
0.4π
【解析】
试题分析:本题实际为两个单摆,从左到右的时间为两个摆总周期的,分别求出两个摆长时的周期大小,即可求得实际摆动中的时间.
小球在摆动过程中,重力沿切向的分力提供回复力;单摆周期公式知:;,摆球从左到右的时间为;
12.
匀速圆周运动;
相对静止.
【解析】
[1].当该升降机以加速度a竖直下降时,则等效重力加速度为;摆的振动周期为。
[2].当摆球摆到最低点时,升降机突然做自由落体运动,完全失重,球将做匀速圆周运动;
[3].当摆球摆到最高点时,升降机突然做自由落体运动,完全失重,故摆球相对于升降机会保持静止;
13.
1
减小
【解析】
[1]由振动图象读出周期
,振幅,由得到角频率
,
则单摆的位移x随时间t变化的关系式为
;
[2]由公式,代入得到
L=1m
;
[3]结合图像可知从到的过程中,摆球向平衡位置运动,所以摆球的位移减小,回复力减小.
14.小于
大于
见解析
【解析】
[1][2]把单摆看作简谐振动时,要忽略空气阻力的影响,重力沿弧线的分力提供回复力;故摆线应细一些并且不可伸长,摆线质量远小于摆球质量,摆线长度远大于摆球直径,摆球要选用体积较小密度大的金属球,以减小空气阻力与摆长变化对实验的影响.
[3]单摆周期公式:
[4]小球在光滑圆弧上的往复运动和单摆的受力情况相同,小球释放高度较小时,这个往复运动就是简谐运动,这时周期公式中的l应该是圆弧半径R.
1.2013年6月,我国宇航员在天宫一号空间站中进行我国首次太空授课活动,展示了许多在地面上无法实现的实验现象.假如要在空间站再次进行授课活动,下列我们曾在实验室中进行的实验,若移到空间站也能够实现操作的有(
)
A.利用托盘天平测质量
B.利用弹簧测力计测拉力
C.利用自由落体验证机械能守恒定律
D.测定单摆做简谐运动的周期
2.一物体在某行星表面受到的万有引力是它在地球表面受到的万有引力的.在地球上走得很准的摆钟搬到此行星上后,此钟的分针走一整圈所经历的实际时间是( )
A.
B.
C.2h
D.4h
3.关于单摆,下列说法中正确的是( )
A.单摆摆球所受的合外力指向平衡位置
B.摆球经过平衡位置时加速度为零
C.摆球运动到平衡位置时,所受回复力等于零
D.摆角很小时,摆球所受合力的大小跟摆球相对平衡位置的位移大小成正比
4.如图所示,光滑圆弧槽半径为
R,
A
为圆弧的最低点,圆弧的最高点到
A
的距离远小于
R。两个可视为质点的小球B
和C
都由静止开始释放。设点
B
到点
A
的距离为
H,则以下所给的四
个H
值中,可以使
B、C
两球在点A
相遇的是(
)
A.
B.
C.
D.
5.如图,长为l的细绳下方悬挂一小球a.绳的另一端固定在天花板上O点处,在O点正下方l的处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x,向右为正.下列图像中,能描述小球在开始一个周期内的x-t关系的是_____.
A.B.C.D.
6.如图所示,长为l的轻绳上端固定在O点,下端系一小球,在O点正下方处的P点固定一小钉子。现将小球拉至A点,使细线与竖直方向间夹角很小,然后由静止释放小球,小球在竖直平面内运动。点B(图中未标出)是小球能够到达的左方最高位置,重力加速度为g,不计空气阻力,下列说法正确的是( )
A.点B在点A下方
B.点B在点A上方
C.小球摆动的周期为
D.小球摆动的周期为
7.如图所示是甲、乙两个单摆做简谐运动的图象,则下列说法中正确的是
A.甲、乙两摆的振幅之比为2:1
B.t=2s时,甲摆的重力势能最小,乙摆的动能为零
C.甲、乙两摆的摆长之比为4:1
D.甲、乙两摆摆球在最低点时摆线的拉力大小一定相等
8.某同学在实验室用单摆测定当地的重力加速度,实验中用游标卡尺测出摆球的直径d,再用米尺测出从悬点至小球上端的悬线长l0;让单摆在竖直平面内做小角度摆动,摆球第一次通过最低点时开始计时,当摆球第N次通过最低点时停止计时,测得时间为t;利用单摆的周期公式计算重力加速度g,变更摆长重做几次,得到g的平均值。该同学发现g的平均值比当地公布的重力加速度的值略大,其原因可能是__。
A.计算摆长时,取l=l0+d
B.计算摆长时,取l=l0
C.计算周期时,取T=
D.实验中,摆线上端未牢固地系于悬点,振动中出现松动
E.实验室地下有重金属矿物质
9.在用单摆测定重力加速度的实验中,下列措施中必要的或做法正确的是______;
A.为了便于计时观察,单摆的摆角应尽量大些
B.摆线长应远远大于摆球直径
C.摆球应选择密度较大的实心金属小球
D.用停表测量周期时,应测量单摆30~50次全振动的时间,然后计算周期,而不能把只测一次全振动时间当作周期
E.将摆球和摆线平放在桌面上,拉直后用米尺测出摆球球心到摆线某点O间的长度作为摆长,然后将O点作为悬点
10.如图所示,用绝缘细线悬挂的单摆,摆球带正电,悬挂于O点,摆长为l,当它摆过竖直线OC时便进入或离开匀强磁场,磁场方向垂直于单摆摆动的平面向里,A,B点分别是最大位移处.下列说法中正确的是( )
A.A点和B点处于同一水平面
B.A点高于B点
C.摆球在A点和B点处线上的拉力大小相等
D.单摆的振动周期仍为
E.单摆向右或向左摆过D点时,线上的拉力大小相等
11.如图,房顶上固定一根长2.5m的细线沿竖直墙壁垂到窗沿下,细线下端系了一个小球(可视为质点)。打开窗子,让小球在垂直于窗子的竖直平面内小幅摆动,窗上沿到房顶的高度为1.6m,不计空气阻力,g取10m/s2,则小球在摆动过程中的回复力是由__________提供的,从最左端运动到最右端的最短时间为________________s。
12.在向下匀速直线运动的升降机中有一摆长为L的单摆在做简谐振动,当该升降机以加速度a
;(升降机内部空气阻力不计,
且最后两空均用文字说明运动情况)
13.如图甲所示,一个单摆做小角度摆动。从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x随时间t变化的图像如图乙所示。不计空气阻力,取。对于这个单摆的振动过程,单摆的位移x随时间t变化的关系式为________cm,单摆的摆长为________m,从t=2.5s到t=3.0s的过程中,摆球所受回复力逐渐________(填“增大”或“减小”)。
14.单摆是一种理想模型,能看做单摆的条件是:摆线不可伸长,摆线质量远______摆球质量,摆线长度远_____________摆球直径(均填“大于”或“小于”)。单摆的摆角小于5°时,可看做简谐运动,此时周期公式是__________。如图所示,在一半径为2.5m的光滑圆轨道上切下一段圆弧,放置于竖直平面内,将一个小钢珠置于圆轨道最低点附近并从静止释放。有同学说,这个小钢珠运动到最低点的最短时间可以用单摆的周期公式去求,他说的有道理吗?请判断并分析说明。______________________
参考答案
1.B
【解析】
天宫一号空间站围绕地球做匀速圆周运动,所受到的万有引力充当了向心力,天宫一号空间站中的物体均处在完全失重状态,所以靠重力作用的实验均不能成功,故只有B选项正确。
故选B.
2.C
【解析】
根据在星球表面万有引力等于重力可知:某行星表面受到的万有引力是它在地球表面受到的万有引力的,质量不变,所以该星球的重力加速度
根据公式
拿到某行星上周期,分针走一圈的时间为地球上的2倍,故C正确,ABD错误。
3.C
【解析】
A.根据回复力的特点可知摆球受到的回复力方向总是指向平衡位置,但合力并不总是指向平衡位置,故A错误;
B.摆球经过平衡位置时,由于做圆周运动,故存在向心加速度,故B错误;
C.摆球运动到平衡位置时,回复力等于零,故C正确;
D.摆角很小时,摆球所受回复力的大小跟摆球对平衡位置的位移大小成正比,而不是合力的大小跟摆球对平衡位置的位移大小成正比,故D错误。
故选C。
4.D
【解析】
对B球,有
解得
对C球,周期为
所以有
由于t=t′,故
解得
(其中:n=0、1、2、3…)
当n=0时,可得
当n=1时,可得
由此可知D符合题意,ABC不符合题意。
5.A
【解析】
由T=2π得:T1=2π,T2=2π=π=T1
,故BD错误;
,
由能量守恒定律可知,小球先后摆起得最大高度相同,故l-lcosθ1=
根据数学规律可得:
故,即第一次振幅是第二次振幅得2倍,故A正确,C错误.
6.D
【解析】
AB.小球摆动过程中,只有重力做功,机械能守恒,可知两侧最高点动能均为零,故重力势能也相等,故最大高度相同,即点B与点A等高,故AB错误;
CD.小球从最低点到A点再到最低点的时间为
小球从最低点到B点再到最低点的时间为
则小球的周期为
故C错误,D正确。
故选D。
7.AB
【解析】
由图知甲、乙两摆的振幅分别为2?cm、1?cm,故选项A正确;t=2?s时,甲摆在平衡位置处重力势能最小;乙摆在振动的最大位移处,动能为零,故选项B正确;甲、乙两摆的周期之比为1:2,由单摆的周期公式T=2π,得到甲、乙两摆的摆长之比为1:4,故选项C错误;由题目的条件不能比较甲、乙两摆摆球在最低点时摆线的拉力大小,故选项D错误;故选AB。
8.ACE
【解析】
由单摆的周期公式可得
A.计算摆长时,取l=l0+d,则摆长测量值偏大,由可知,重力加速度测量值偏大,故A正确;
B.计算摆长时,取l=l0时,则摆长测值偏小,由可知,重力加速度测量值偏小,故B错误;
C.计算周期时,取T=则周期偏小,由可知,重力加速度测量值偏大,故C正确;
D.实验中,摆线上端未牢固地系于悬点,振动中出现松动,则摆长测量值偏小,由可知,重力加速度测量值偏小,故D错误;
E.实验室地下有重金属矿物质,小球受到地球的引力增大,则重力加速度偏大,故E正确。
故选ACE。
9.BCD
【解析】
A.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过5°,否则单摆将不做简谐运动,故A错误;
BC.为了减小空气阻力的影响,摆球的直径应远小于摆线的长度,并选择密度较大的实心金属小球作为摆球,故BC正确;
D.为了减小测量误差,应采用累积法测量周期,即测量单摆30~50次全振动的时间t,再求出周期T,故D正确;
E.这样做很难保证悬点就是O点,就会导致摆长测量不准确,应将单摆悬点固定后,用米尺测出摆球球心到悬点的距离作为摆长,所以E错误。
故选BCD。
10.ACD
【解析】
摆球运动过程中机械能守恒,所以A,B在同一高度.选项A正确,B错误;球在B点不受洛伦兹力,与球在A点时受拉力大小相等,选项C正确;球在磁场中运动时虽然受洛伦兹力,但洛伦兹力总与速度方向垂直,不能提供回复力,所以不改变振动的周期,选项D正确;单摆向右或向左摆过D点时,速度大小相等,但洛伦兹力的方向相反,所以线上的拉力不相等,选项E错误.
【点睛】本题中小球在复合场运动,洛伦兹力不做功,其机械能仍然守恒,洛伦兹力不改变小球运动的快慢.但要注意洛伦兹力方向与速度有关,速度反向,洛伦兹力方向也相反.
11.重力沿切线方向的分力(或重力沿运动方向的分力)
0.4π
【解析】
试题分析:本题实际为两个单摆,从左到右的时间为两个摆总周期的,分别求出两个摆长时的周期大小,即可求得实际摆动中的时间.
小球在摆动过程中,重力沿切向的分力提供回复力;单摆周期公式知:;,摆球从左到右的时间为;
12.
匀速圆周运动;
相对静止.
【解析】
[1].当该升降机以加速度a
[2].当摆球摆到最低点时,升降机突然做自由落体运动,完全失重,球将做匀速圆周运动;
[3].当摆球摆到最高点时,升降机突然做自由落体运动,完全失重,故摆球相对于升降机会保持静止;
13.
1
减小
【解析】
[1]由振动图象读出周期
,振幅,由得到角频率
,
则单摆的位移x随时间t变化的关系式为
;
[2]由公式,代入得到
L=1m
;
[3]结合图像可知从到的过程中,摆球向平衡位置运动,所以摆球的位移减小,回复力减小.
14.小于
大于
见解析
【解析】
[1][2]把单摆看作简谐振动时,要忽略空气阻力的影响,重力沿弧线的分力提供回复力;故摆线应细一些并且不可伸长,摆线质量远小于摆球质量,摆线长度远大于摆球直径,摆球要选用体积较小密度大的金属球,以减小空气阻力与摆长变化对实验的影响.
[3]单摆周期公式:
[4]小球在光滑圆弧上的往复运动和单摆的受力情况相同,小球释放高度较小时,这个往复运动就是简谐运动,这时周期公式中的l应该是圆弧半径R.
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
