冀教版数学四年级上册4 线和角 第四课时 平角、周角以及各种角的关系的认识 教案
文档属性
| 名称 | 冀教版数学四年级上册4 线和角 第四课时 平角、周角以及各种角的关系的认识 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 218.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 11:16:49 | ||
图片预览


文档简介
4.4
平角、周角以及各种角的关系的认识
教学内容
教材第43、44页
平角、周角以及各种角的关系的认识
教学提示
教材设计了两个操作活动。活动一,折纸。由于平角、周角比较抽象,难于理解,所以教材设计了折纸活动,由学生的折纸活动和运用已有的知识,先认识平角,再认识周角,通过学生的折纸、观察、测量、交流活动,直观认识平角、周角的大小和特征。即两个直角组成一个平角,平角是180°;四个直角组成一个周角,周角是360°;然后教材设计了“议一议”的两个问题,通过学生的讨论和交流知道直角、周角和平角的关系。接着,通过在打开的圆形折扇上找角、画出角、认识平角和周角。活动二,操作和观察活动。在学生分别认识了各种角之后,通过操作活动角来认识各种角的大小关系,学生通过自己的操作,观察和交流,进一步认识锐角、钝角的量化范围体验并知道各种角的大小和它们之间的关系。
教学时,教师让学生更加直观地看到角的形成过程,体验归纳各种角的特征;充分体验数学与生活的紧密联系;同时教师要发掘学生的肢体语言的丰富内涵来帮助学生理解平角、周角以及各种角之间的关系。
教学目标
知识与能力
认识平角和周角,知道锐角、直角、钝角、平角、周角之间的大小关系。
会根据角的度数区分直角、锐角、钝角、平角和周角。
过程与方法
在动手折角、用活动角作角的过程中,认识各种角以及它们之间的关系。
2、通过学生活动,培养动手操作、合作学习与探究学习的能力,发展空间观念。
情感、态度与价值观
体验数学与日常生活的密切联系,培养探索数学奥秘的兴趣,渗透事物间是变化的、联系的思想。
重点、难点
重点
认识平角和周角,知道直角、平角、周角之间的关系。
难点
认识几种常见的角,理解它们之间的关系。
教学准备
教师准备:长方形卡纸、圆扇、量角器、活动角。
学生准备:长方形卡纸、
圆扇、量角器、活动角。
教学过程
(一)新课导入
师:角有什么特征?今天老师想考考同学们的记忆力,拿出一张白纸演示,像老师这样对折一次,再对折一次。
师:指着角问同学:“这是什么角?你是怎么知道的?”?
(预设)
生1:直角。
生2:量角器量的?。?
生3:三角板可以对比发现直角等于90度。
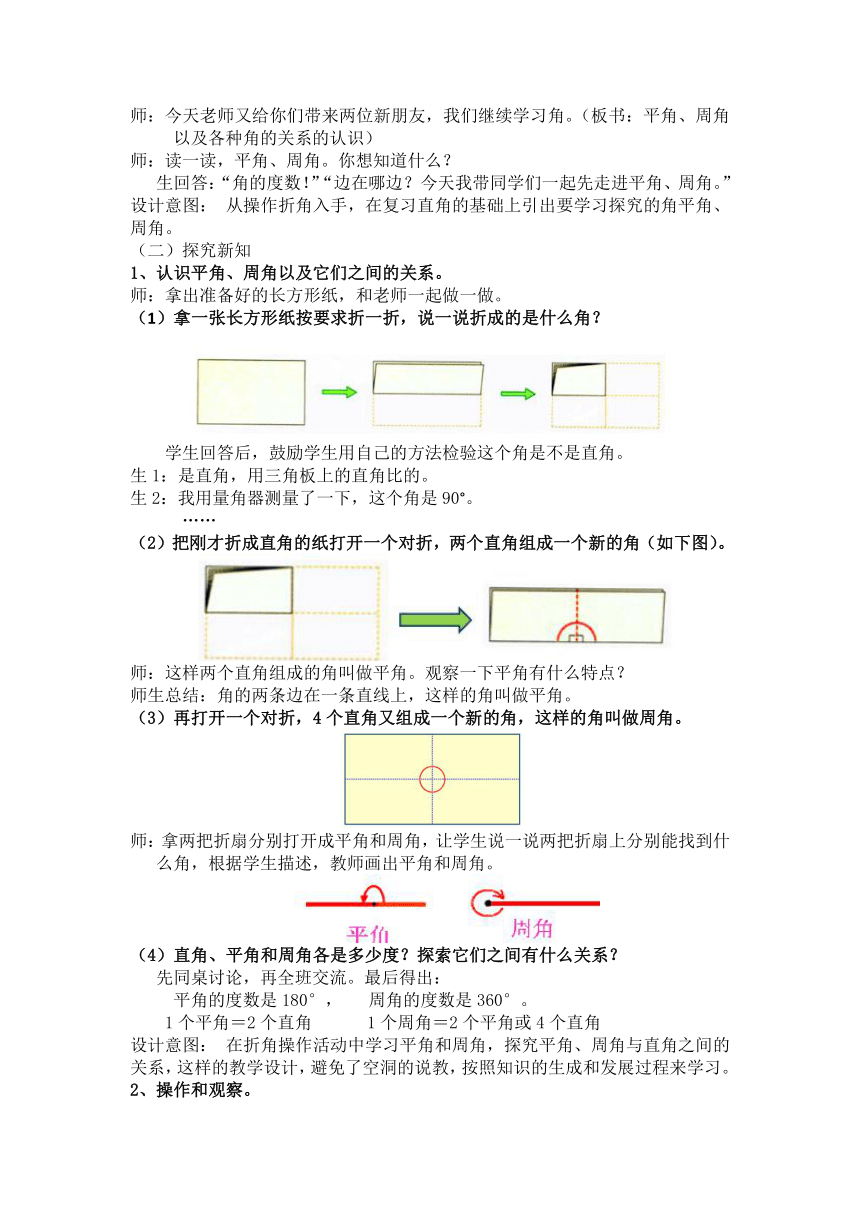
师:今天老师又给你们带来两位新朋友,我们继续学习角。(板书:平角、周角以及各种角的关系的认识)
师:读一读,平角、周角。你想知道什么?
生回答:“角的度数!”“边在哪边?今天我带同学们一起先走进平角、周角。”
设计意图:
从操作折角入手,在复习直角的基础上引出要学习探究的角平角、周角。
(二)探究新知
1、认识平角、周角以及它们之间的关系。
师:拿出准备好的长方形纸,和老师一起做一做。
(1)拿一张长方形纸按要求折一折,说一说折成的是什么角??
学生回答后,鼓励学生用自己的方法检验这个角是不是直角。?
生1:是直角,用三角板上的直角比的。?
生2:我用量角器测量了一下,这个角是90°。
……
(2)把刚才折成直角的纸打开一个对折,两个直角组成一个新的角(如下图)。?
师:这样两个直角组成的角叫做平角。观察一下平角有什么特点?
师生总结:角的两条边在一条直线上,这样的角叫做平角。?
(3)再打开一个对折,4个直角又组成一个新的角,这样的角叫做周角。
师:拿两把折扇分别打开成平角和周角,让学生说一说两把折扇上分别能找到什么角,根据学生描述,教师画出平角和周角。?
(4)直角、平角和周角各是多少度?探索它们之间有什么关系??
先同桌讨论,再全班交流。最后得出:
平角的度数是180°,
周角的度数是360°。?
1个平角=2个直角?
??1个周角=2个平角或4个直角?
设计意图:
在折角操作活动中学习平角和周角,探究平角、周角与直角之间的关系,这样的教学设计,避免了空洞的说教,按照知识的生成和发展过程来学习。
2、操作和观察。
师:用一个活动角,边操作,边观察,说说各是什么角。?
(1)认识锐角和钝角。
①让学生按图示从小到大操作活动角,学生边操作边观察,回答做出的是什么角。同时画出各角。?
②让学生观察画出的角,并说一说哪个度数范围内的角叫锐角,哪个度数范围内的角叫钝角。?
锐角:小于90°
钝角
大于90°而小于180°
师生共同总结出锐角和钝角的定义。?
小于90°的角叫做锐角,大于90°而小于180°的角叫做钝角。?
(2)延伸拓展。
师:举出具体度数的角让学生判断角的种类。
78°???89°???180°??100°???101°??91°???189°????270°
设计意图:
在操作活动中认识锐角和钝角,这样在操作中沟通锐角、钝角、直角、平角和周角之间的关系。
(三)巩固新知
1、教材第44页“练一练”第1、2题。
2、教材第44页“练一练”第3题。
设计意图:
1、在钟面上画时针和分针,在画时针的过程中,体验和理解直角、锐角、钝角和平角的含义和意义。
2、在观察和理解平角意义的基础上,完成填空,进一步体验、理解和感悟平角的意义。
(四)达标反馈
1、细心认真填一填。
(1)一直角=(
)°
一平角=(
)直角
=(
)°
(2)一周角=(
)平角=(
)直角=(
)°
2、判断。
(1)平角就是一条直线。(
)
(2)大于90°的角是钝角。(
)
(3)按照角的大小排列:周角>平角>钝角>直角>锐角。
(4)6时整,时针和分针所成的角是平角。
(5)周角就是一条射线。(
)
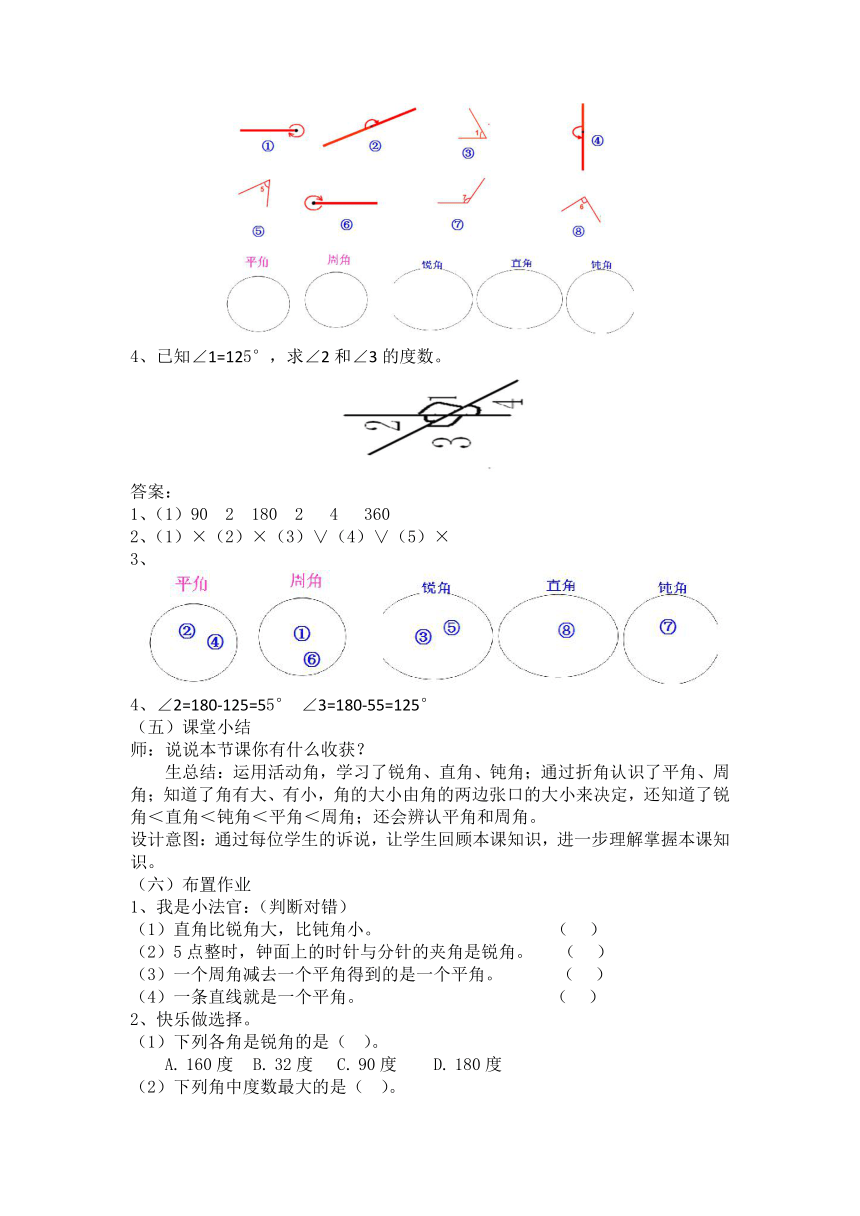
3、帮角找回家。
4、已知∠1=125°,求∠2和∠3的度数。
答案:
1、(1)90
2
180
2
4
360
2、(1)×(2)×(3)∨(4)∨(5)×
3、
4、∠2=180-125=55°
∠3=180-55=125°
(五)课堂小结
师:说说本节课你有什么收获?
生总结:运用活动角,学习了锐角、直角、钝角;通过折角认识了平角、周角;知道了角有大、有小,角的大小由角的两边张口的大小来决定,还知道了锐角<直角<钝角<平角<周角;还会辨认平角和周角。
设计意图:通过每位学生的诉说,让学生回顾本课知识,进一步理解掌握本课知识。
(六)布置作业
1、我是小法官:(判断对错)
(1)直角比锐角大,比钝角小。???????????????????
(???
)
(2)5点整时,钟面上的时针与分针的夹角是锐角。??
(???
)?
(3)一个周角减去一个平角得到的是一个平角。??
?
??(???
)?
(4)一条直线就是一个平角。?????????????????????
(???
)
2、快乐做选择。
(1)下列各角是锐角的是(????)。?
A.?160度?????B.?32度??????C.?90度???????
D.?180度?
(2)下列角中度数最大的是(????)。?
A.?平角??????B.?锐角???????C.?钝角????????D.?周角
?(3)直角的一半是(????)。?
A.?90度??????B.?30度??????C.?45度????????D.?180度?
(4)钝角比(????)小。?
A.?直角??????B.?平角???????C.?锐角?????????D.?80度角?
(5)平角的度数是(????)的2倍。?
A.?锐角??????B.?钝角???????
C.?直角?????????D.?周角?
3、把以下5种角按从小到大的顺序排列。?
直角???锐角???钝角???周角???平角
4、把角送回家。
7°、92°、179°、38°、89°、180°、
100°、57°、360°、160°、90°
5、做一个活动角,照下图的次序转动其中的一条边,依次写出得到的是什么角。
6、下面两个图中的∠1与∠2是不是相等?说明理由。
答案:
1、(1)∨(2)×(3)∨(4)×
2、(1)B
(2)D
(3)C
(4)B
(5)C
3、锐角
直角?
钝角
平角
周角???
4、
5、锐角
直角
钝角
平角
周角
6、∠1=∠2
∠1=∠2
板书设计
教学资料包
教学精彩片段
探究平角和周角教学片断
1、操作活动,探究平角。
师:(手拿旋转角,大于90°)还能继续旋转吗?师演示,当两条边在一条直线上后,问,这是一个角吗?请同桌交流讨论。
(预设)
生1:不是角。
生2:是角。
(分别让学生说说为什么)
师生共同探讨:符合一个角的条件是什么?
(预设)
生:一个顶点和从这个顶点引出的两条边。
师:观察教具图,有几个顶点?几条边呢?那么它是一个角吗?这个角有什么特点?
揭示名称:平角。(师板书平角名称及特点:两条边在一条直线上)
师:请同学们旋转出一个平角。
师:这是平角吗?(师摆出不同方向的平角)
结论:不管平角放成什么方向,只要有一个顶点,从这个顶点引出的两条射线在一条直线上,那么这个角就是平角。
师:那么怎样画出这个平角呢?指出先画顶点,再画出从顶点引出的两条边,最后标出旋转的方向。
学生按照老师的提示画出平角。
让学生比较钝角和平角,发现平角比钝角大的特点;比较平角和直角,发现它们之间的关系:1个平角=2个直角。
2、实践操作,探究周角。
师:我们继续旋转,看看还能旋转出其他的角吗?
当两条边重合后,问,这是一个角吗?(同探究平角的方法)
结论:1个周角=2个平角????
1个周角=4个直角
设计意图:平角与周角的认识是由教师演示得到的,所以这里安排了让学生旋转自己手中的活动角得到平角与周角,目的是要让学生通过自己动手旋转,从而体验平角与周角的形成过程。平角和周角的画法不是本课的难点,同时它们的画法必须规范化,所以这个环节的设计是教师先讲清楚平角的画法,再让学生画,而周角则由教师先演示,再让学生去画,这样大大提高了课堂的效率。
教学资源
角的种类
角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种。以度、分、秒为单位的角的度量制称为角度制。此外,还有密位制、弧度制等。
锐角(acute
angle):大于0°,小于90°的角叫做锐角。
直角(right
angle):等于90°的角叫做直角。
钝角(obtuse
angle):大于90°而小于180°的角叫做钝角。
平角(flat
angle):等于180°的角叫做平角。
优角(reflex
angle):大于180°小于360°叫优角。
劣角(Inferior
angle):大于0°小于180°叫做劣角,锐角、直角、钝角都是劣角。
周角(round
angle):等于360°的角叫做周角。
负角(negative
angle):按照顺时针方向旋转而成的角叫做负角。
正角(positive
angle):逆时针旋转的角为正角。
零角(zero
angle):等于0°的角。
资料链接
正角和负角
角在一些应用时,会将角的数值加上正负号,以标明是相对参考物不同方向的旋转。
在二维的笛卡尔坐标系中,角一般是以x轴的正向为基准,若往y轴的正向旋转,则其角为正角,若往y轴的负向旋转,则其角为负角。若二维的笛卡儿坐标系也是x轴朝右,y轴朝上,则逆时针的旋转对应正角,顺时针的旋转对应负角。
一般而言,?θ角和一圈减去θ所得的角是相同的。例如
?
45°和360°
?
45°(=315°)等效,但这只适用在用角表示相对位置,不是旋转概念时。旋转?
45°和旋转315°是不同的。
在三维的几何中,顺时针及逆时针没有绝对的定义,因此定义正角及负角时均需列出其参考的基准,一般会以一个通过角的顶点,和角所在平面垂直的向量为基准。
在导航时,导向是以北方为基准,正向表示顺时针,因此导向45°对应东北方。导向没有负值,西北方对应的导向为315°。
童话故事----角的来历
小圆点是天空中最快乐的成员,可是有一天,它和太阳公公玩,一不小心,“啪”地从空中摔了下来,还把太阳公公的两根胡须扯下来了。
“这可怎么办呢?”小圆点对躺在地上的两条射线说。?这时,圆规大叔来了。对小圆点说:“不要紧,我来把你和两条射线接起来,不过,连起来就不见得是一条直线了。”?
“那是怎么回事呀?”小圆点问。
“你看。”圆规大叔边说边拉起两条射线,把它们连在一起,结果呢?(看下图)?
?
小圆点惊叫了一声,“这是什么呀?怎么还有一个拐角呢?”
?圆规大叔告诉它,“这是角,尖尖的地方也就是你所在的点,叫做角的顶点,从角的顶点引出的两条射线叫做角的边。”?
小圆点很高兴自己又有了一个新名字。
平角、周角以及各种角的关系的认识
教学内容
教材第43、44页
平角、周角以及各种角的关系的认识
教学提示
教材设计了两个操作活动。活动一,折纸。由于平角、周角比较抽象,难于理解,所以教材设计了折纸活动,由学生的折纸活动和运用已有的知识,先认识平角,再认识周角,通过学生的折纸、观察、测量、交流活动,直观认识平角、周角的大小和特征。即两个直角组成一个平角,平角是180°;四个直角组成一个周角,周角是360°;然后教材设计了“议一议”的两个问题,通过学生的讨论和交流知道直角、周角和平角的关系。接着,通过在打开的圆形折扇上找角、画出角、认识平角和周角。活动二,操作和观察活动。在学生分别认识了各种角之后,通过操作活动角来认识各种角的大小关系,学生通过自己的操作,观察和交流,进一步认识锐角、钝角的量化范围体验并知道各种角的大小和它们之间的关系。
教学时,教师让学生更加直观地看到角的形成过程,体验归纳各种角的特征;充分体验数学与生活的紧密联系;同时教师要发掘学生的肢体语言的丰富内涵来帮助学生理解平角、周角以及各种角之间的关系。
教学目标
知识与能力
认识平角和周角,知道锐角、直角、钝角、平角、周角之间的大小关系。
会根据角的度数区分直角、锐角、钝角、平角和周角。
过程与方法
在动手折角、用活动角作角的过程中,认识各种角以及它们之间的关系。
2、通过学生活动,培养动手操作、合作学习与探究学习的能力,发展空间观念。
情感、态度与价值观
体验数学与日常生活的密切联系,培养探索数学奥秘的兴趣,渗透事物间是变化的、联系的思想。
重点、难点
重点
认识平角和周角,知道直角、平角、周角之间的关系。
难点
认识几种常见的角,理解它们之间的关系。
教学准备
教师准备:长方形卡纸、圆扇、量角器、活动角。
学生准备:长方形卡纸、
圆扇、量角器、活动角。
教学过程
(一)新课导入
师:角有什么特征?今天老师想考考同学们的记忆力,拿出一张白纸演示,像老师这样对折一次,再对折一次。
师:指着角问同学:“这是什么角?你是怎么知道的?”?
(预设)
生1:直角。
生2:量角器量的?。?
生3:三角板可以对比发现直角等于90度。
师:今天老师又给你们带来两位新朋友,我们继续学习角。(板书:平角、周角以及各种角的关系的认识)
师:读一读,平角、周角。你想知道什么?
生回答:“角的度数!”“边在哪边?今天我带同学们一起先走进平角、周角。”
设计意图:
从操作折角入手,在复习直角的基础上引出要学习探究的角平角、周角。
(二)探究新知
1、认识平角、周角以及它们之间的关系。
师:拿出准备好的长方形纸,和老师一起做一做。
(1)拿一张长方形纸按要求折一折,说一说折成的是什么角??
学生回答后,鼓励学生用自己的方法检验这个角是不是直角。?
生1:是直角,用三角板上的直角比的。?
生2:我用量角器测量了一下,这个角是90°。
……
(2)把刚才折成直角的纸打开一个对折,两个直角组成一个新的角(如下图)。?
师:这样两个直角组成的角叫做平角。观察一下平角有什么特点?
师生总结:角的两条边在一条直线上,这样的角叫做平角。?
(3)再打开一个对折,4个直角又组成一个新的角,这样的角叫做周角。
师:拿两把折扇分别打开成平角和周角,让学生说一说两把折扇上分别能找到什么角,根据学生描述,教师画出平角和周角。?
(4)直角、平角和周角各是多少度?探索它们之间有什么关系??
先同桌讨论,再全班交流。最后得出:
平角的度数是180°,
周角的度数是360°。?
1个平角=2个直角?
??1个周角=2个平角或4个直角?
设计意图:
在折角操作活动中学习平角和周角,探究平角、周角与直角之间的关系,这样的教学设计,避免了空洞的说教,按照知识的生成和发展过程来学习。
2、操作和观察。
师:用一个活动角,边操作,边观察,说说各是什么角。?
(1)认识锐角和钝角。
①让学生按图示从小到大操作活动角,学生边操作边观察,回答做出的是什么角。同时画出各角。?
②让学生观察画出的角,并说一说哪个度数范围内的角叫锐角,哪个度数范围内的角叫钝角。?
锐角:小于90°
钝角
大于90°而小于180°
师生共同总结出锐角和钝角的定义。?
小于90°的角叫做锐角,大于90°而小于180°的角叫做钝角。?
(2)延伸拓展。
师:举出具体度数的角让学生判断角的种类。
78°???89°???180°??100°???101°??91°???189°????270°
设计意图:
在操作活动中认识锐角和钝角,这样在操作中沟通锐角、钝角、直角、平角和周角之间的关系。
(三)巩固新知
1、教材第44页“练一练”第1、2题。
2、教材第44页“练一练”第3题。
设计意图:
1、在钟面上画时针和分针,在画时针的过程中,体验和理解直角、锐角、钝角和平角的含义和意义。
2、在观察和理解平角意义的基础上,完成填空,进一步体验、理解和感悟平角的意义。
(四)达标反馈
1、细心认真填一填。
(1)一直角=(
)°
一平角=(
)直角
=(
)°
(2)一周角=(
)平角=(
)直角=(
)°
2、判断。
(1)平角就是一条直线。(
)
(2)大于90°的角是钝角。(
)
(3)按照角的大小排列:周角>平角>钝角>直角>锐角。
(4)6时整,时针和分针所成的角是平角。
(5)周角就是一条射线。(
)
3、帮角找回家。
4、已知∠1=125°,求∠2和∠3的度数。
答案:
1、(1)90
2
180
2
4
360
2、(1)×(2)×(3)∨(4)∨(5)×
3、
4、∠2=180-125=55°
∠3=180-55=125°
(五)课堂小结
师:说说本节课你有什么收获?
生总结:运用活动角,学习了锐角、直角、钝角;通过折角认识了平角、周角;知道了角有大、有小,角的大小由角的两边张口的大小来决定,还知道了锐角<直角<钝角<平角<周角;还会辨认平角和周角。
设计意图:通过每位学生的诉说,让学生回顾本课知识,进一步理解掌握本课知识。
(六)布置作业
1、我是小法官:(判断对错)
(1)直角比锐角大,比钝角小。???????????????????
(???
)
(2)5点整时,钟面上的时针与分针的夹角是锐角。??
(???
)?
(3)一个周角减去一个平角得到的是一个平角。??
?
??(???
)?
(4)一条直线就是一个平角。?????????????????????
(???
)
2、快乐做选择。
(1)下列各角是锐角的是(????)。?
A.?160度?????B.?32度??????C.?90度???????
D.?180度?
(2)下列角中度数最大的是(????)。?
A.?平角??????B.?锐角???????C.?钝角????????D.?周角
?(3)直角的一半是(????)。?
A.?90度??????B.?30度??????C.?45度????????D.?180度?
(4)钝角比(????)小。?
A.?直角??????B.?平角???????C.?锐角?????????D.?80度角?
(5)平角的度数是(????)的2倍。?
A.?锐角??????B.?钝角???????
C.?直角?????????D.?周角?
3、把以下5种角按从小到大的顺序排列。?
直角???锐角???钝角???周角???平角
4、把角送回家。
7°、92°、179°、38°、89°、180°、
100°、57°、360°、160°、90°
5、做一个活动角,照下图的次序转动其中的一条边,依次写出得到的是什么角。
6、下面两个图中的∠1与∠2是不是相等?说明理由。
答案:
1、(1)∨(2)×(3)∨(4)×
2、(1)B
(2)D
(3)C
(4)B
(5)C
3、锐角
直角?
钝角
平角
周角???
4、
5、锐角
直角
钝角
平角
周角
6、∠1=∠2
∠1=∠2
板书设计
教学资料包
教学精彩片段
探究平角和周角教学片断
1、操作活动,探究平角。
师:(手拿旋转角,大于90°)还能继续旋转吗?师演示,当两条边在一条直线上后,问,这是一个角吗?请同桌交流讨论。
(预设)
生1:不是角。
生2:是角。
(分别让学生说说为什么)
师生共同探讨:符合一个角的条件是什么?
(预设)
生:一个顶点和从这个顶点引出的两条边。
师:观察教具图,有几个顶点?几条边呢?那么它是一个角吗?这个角有什么特点?
揭示名称:平角。(师板书平角名称及特点:两条边在一条直线上)
师:请同学们旋转出一个平角。
师:这是平角吗?(师摆出不同方向的平角)
结论:不管平角放成什么方向,只要有一个顶点,从这个顶点引出的两条射线在一条直线上,那么这个角就是平角。
师:那么怎样画出这个平角呢?指出先画顶点,再画出从顶点引出的两条边,最后标出旋转的方向。
学生按照老师的提示画出平角。
让学生比较钝角和平角,发现平角比钝角大的特点;比较平角和直角,发现它们之间的关系:1个平角=2个直角。
2、实践操作,探究周角。
师:我们继续旋转,看看还能旋转出其他的角吗?
当两条边重合后,问,这是一个角吗?(同探究平角的方法)
结论:1个周角=2个平角????
1个周角=4个直角
设计意图:平角与周角的认识是由教师演示得到的,所以这里安排了让学生旋转自己手中的活动角得到平角与周角,目的是要让学生通过自己动手旋转,从而体验平角与周角的形成过程。平角和周角的画法不是本课的难点,同时它们的画法必须规范化,所以这个环节的设计是教师先讲清楚平角的画法,再让学生画,而周角则由教师先演示,再让学生去画,这样大大提高了课堂的效率。
教学资源
角的种类
角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种。以度、分、秒为单位的角的度量制称为角度制。此外,还有密位制、弧度制等。
锐角(acute
angle):大于0°,小于90°的角叫做锐角。
直角(right
angle):等于90°的角叫做直角。
钝角(obtuse
angle):大于90°而小于180°的角叫做钝角。
平角(flat
angle):等于180°的角叫做平角。
优角(reflex
angle):大于180°小于360°叫优角。
劣角(Inferior
angle):大于0°小于180°叫做劣角,锐角、直角、钝角都是劣角。
周角(round
angle):等于360°的角叫做周角。
负角(negative
angle):按照顺时针方向旋转而成的角叫做负角。
正角(positive
angle):逆时针旋转的角为正角。
零角(zero
angle):等于0°的角。
资料链接
正角和负角
角在一些应用时,会将角的数值加上正负号,以标明是相对参考物不同方向的旋转。
在二维的笛卡尔坐标系中,角一般是以x轴的正向为基准,若往y轴的正向旋转,则其角为正角,若往y轴的负向旋转,则其角为负角。若二维的笛卡儿坐标系也是x轴朝右,y轴朝上,则逆时针的旋转对应正角,顺时针的旋转对应负角。
一般而言,?θ角和一圈减去θ所得的角是相同的。例如
?
45°和360°
?
45°(=315°)等效,但这只适用在用角表示相对位置,不是旋转概念时。旋转?
45°和旋转315°是不同的。
在三维的几何中,顺时针及逆时针没有绝对的定义,因此定义正角及负角时均需列出其参考的基准,一般会以一个通过角的顶点,和角所在平面垂直的向量为基准。
在导航时,导向是以北方为基准,正向表示顺时针,因此导向45°对应东北方。导向没有负值,西北方对应的导向为315°。
童话故事----角的来历
小圆点是天空中最快乐的成员,可是有一天,它和太阳公公玩,一不小心,“啪”地从空中摔了下来,还把太阳公公的两根胡须扯下来了。
“这可怎么办呢?”小圆点对躺在地上的两条射线说。?这时,圆规大叔来了。对小圆点说:“不要紧,我来把你和两条射线接起来,不过,连起来就不见得是一条直线了。”?
“那是怎么回事呀?”小圆点问。
“你看。”圆规大叔边说边拉起两条射线,把它们连在一起,结果呢?(看下图)?
?
小圆点惊叫了一声,“这是什么呀?怎么还有一个拐角呢?”
?圆规大叔告诉它,“这是角,尖尖的地方也就是你所在的点,叫做角的顶点,从角的顶点引出的两条射线叫做角的边。”?
小圆点很高兴自己又有了一个新名字。
