人教版九年级数学上册24.1.1 -圆-同步练习(含解析)
文档属性
| 名称 | 人教版九年级数学上册24.1.1 -圆-同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 401.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-06 00:00:00 | ||
图片预览




文档简介
24.1.1
圆
基础闯关全练
1.到圆心的距离不大于半径的点的集合是(
)
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
2.(2018北京顺义一模)如图24
-1-1-1所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2
cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是(
)
A.1
cm
B.2
c.m
C.4
cm
D.πcm
3.已知:如图24-1-1-2,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
4.(2019江苏无锡江阴月考)下列说法错误的是(
)
A.长度相等的两条弧是等弧
B.直径是圆中最长的弦
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
5.(2018山东菏泽单县期末)如图24-1-1-3,在⊙O中,弦的条数是(
)
A.2
3
4
D.以上均不正确
能力提升全练
1.有一半圆片,点E为圆心,∠AED=
52°,在平面直角坐标系中,按如图24-1-1-4所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O之间的距离最大,则n的值为(
)
A.64
B.52
C.38
D.26
2.如图24
-
1-1-5,在以原点为圆心,2为半径的⊙O上有一点C,∠COA
=45°,则C的坐标为(
)
(,)
B.(,-)
C.(-,)
D.(-,-)
3.如图24-1-1-6,在以原点为圆心的⊙O上有一点C,若点C的坐标为(2,-1),则直径AB的长是________.
4.如图24-1-1-7,正方形ABCD的边长为1,其中,的圆心依次是点A,B,C.连接GB和FD,则GB与FD的关系是________.
三年模拟全练
一、选择题
1.(2019湖南长沙天心明德中学月考,3,★☆☆)下列说法中,错误的是(
)
A.半圆是弧
B.半径相等的圆是等圆
C.过圆心的线段是直径
D.直径是弦
二、填空题
2.(2019江苏淮安期中,16,★☆☆)如图24-1-1-8,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=
40°,∠OBC=50°,则∠OAC=______________°.
五年中考全练
一、选择题
1.(2018辽宁阜新中考,6,★☆☆)如图24-1-1-9,AB是⊙O的直径,点C在圆上,∠ABC=
65°,那么∠OCA的度数是(
)
A.25°
B.35°
C.15°
D.20°
二、填空题
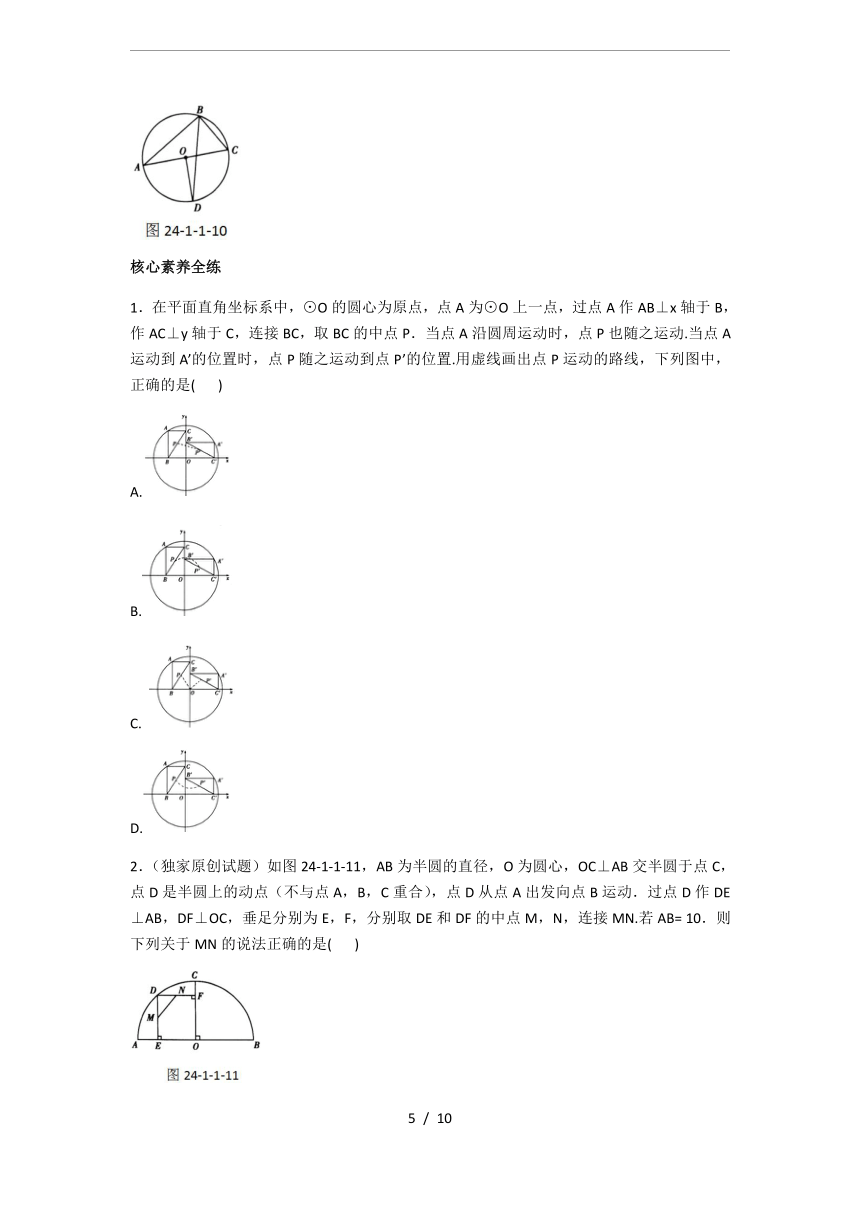
2.(2018黑龙江龙东中考,6,★☆☆)如图24-1-1-10,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=
15°,则∠ACB=________.
核心素养全练
1.在平面直角坐标系中,⊙O的圆心为原点,点A为⊙O上一点,过点A作AB⊥x轴于B,作AC⊥y轴于C,连接BC,取BC的中点P.当点A沿圆周运动时,点P也随之运动.当点A运动到A’的位置时,点P随之运动到点P’的位置.用虚线画出点P运动的路线,下列图中,正确的是(
)
A.
B.
C.
D.
2.(独家原创试题)如图24-1-1-11,AB为半圆的直径,O为圆心,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=
10.则下列关于MN的说法正确的是(
)
先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
答案
基础闯关全练
1.D
圆的内部是到圆心的距离小于半径的所有点的集合,圆是到圆心的距离等于半径的所有点的集合,故到圆心的距离不大于半径的点的集合是圆的内部和圆.故选D.
2.C
∵点A与点B的距离是2
cm,即半径是2
cm,∴圆的直径是4
cm.故选C.
3.证明如图,连接ME、MD,
∵BD、CE是△ABC的高,
∴∠BEC=
∠BDC=90?,
∵M为BC的中点,
∴ME=MD=MC=MB=BC.
∴点B、C、D、E在以点M为圆心的同一个圆上.
4.A
长度相等的弧所对圆心角的度数不一定相等,只有互相重合的弧才是等弧,故A中说法错误;选项B、C、D中说法都正确,故选A.
5.C
题图中共有4条弦,分别是弦AB、弦DB、弦CB、弦CD.故选C.
能力提升全练
1.D
如图,连接OE、OD,当点O、E、D共线时,半圆片上的点D与原点O之间的距离最大,则∠AED=
∠EAO+
∠EOA,在Rt△AOB中,因为AE=
EB,所以EA=
EO=
EB,所以∠EAO=∠EOA,所以
n°=∠AED=26°.故选D.
2.C
如图,过C作CB⊥OA于点B,
∵∠COA=45?,
∴三角形BCO为等腰直角三角形.
∵OC=2.∴OB=BC=.
又∵点C位于第二象限,
∴点C的坐标为(,),故选C.
3.答案
解析
如图,作CD⊥AB于点D,连接OC,则CD=1,OD=2.在Rt△OCD中,.∴AB=
2OC=
.
4.答案
相等且互相垂直
解析
∵BC=DC,CG=
CF,
又∠FCD=
∠GCB=90°,
∴△FCD≌△GCB,
∴GB=
FD,∠G=∠F,
∴
∠G+∠CDF=∠F+∠CDF=90°,
即GB与FD的关系是相等且互相垂直.
三年模拟全练
一、选择题
1.C
过圆心的弦为直径,所以C选项的说法错误;选项A、B、D的说法都正确,故选C.
二、填空题
2.答案
30
解析
如图,连接OC,∵OC=
OB,∠OBC=50°,∴∠OCB=∠OBC=50°,
∴∠BOC=
180?-50?×2=80?,
∴∠AOB=
40°.
∴∠AOC=80°+40°=120°,∵OC=OA,
∴∠OAC=∠OCA=
30°.
五年中考全练
一、选择题
1.A
∵OB=
OC,
∠ABC=
65°,∴∠OCB=
65°,∴∠BOC=
180°-65°×2=
50°,∵AB是⊙O的直径,OA=OC,∴∠OCA=∠OAC=∠BOC=×50°=25°,故选A.
二、填空题
2.答案
60°
解析
如图,连接DC,OB,∵∠BDO=
15°,OB=OD,∴∠OBD=∠BDO=
15°,∴∠BOD=
150°.∵OD⊥AC,∴∠DOC=
90°,∴∠BOC=150°-90°=
60°,又OB=
OC,∴△BOC是等边三角形,∴∠ACB=60°.
核心素养全练
1.B连接OP,OP’,由题意可知BC=B'C'=半径,则OP=
OP’=BC,在点A的运动过程中,OP的长不变,∴点P运动的路线是以点O为圆心,OP为半径的圆的一段弧,故选B.
2.D如图,连接OD,EF,∵AB=
10,∴OD=5.∵DE⊥AB,DF⊥OC,OC⊥AB,∴四边形DEOF是矩形,∴EF=OD=5.当点D在半圆上运动时,由圆上各点到圆心的距离都等于半径,可知OD的长不变,∵点M,N分别为DE和DF的中点,∴MN=EF=OD=2.5.
/
圆
基础闯关全练
1.到圆心的距离不大于半径的点的集合是(
)
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
2.(2018北京顺义一模)如图24
-1-1-1所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2
cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是(
)
A.1
cm
B.2
c.m
C.4
cm
D.πcm
3.已知:如图24-1-1-2,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
4.(2019江苏无锡江阴月考)下列说法错误的是(
)
A.长度相等的两条弧是等弧
B.直径是圆中最长的弦
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
5.(2018山东菏泽单县期末)如图24-1-1-3,在⊙O中,弦的条数是(
)
A.2
3
4
D.以上均不正确
能力提升全练
1.有一半圆片,点E为圆心,∠AED=
52°,在平面直角坐标系中,按如图24-1-1-4所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O之间的距离最大,则n的值为(
)
A.64
B.52
C.38
D.26
2.如图24
-
1-1-5,在以原点为圆心,2为半径的⊙O上有一点C,∠COA
=45°,则C的坐标为(
)
(,)
B.(,-)
C.(-,)
D.(-,-)
3.如图24-1-1-6,在以原点为圆心的⊙O上有一点C,若点C的坐标为(2,-1),则直径AB的长是________.
4.如图24-1-1-7,正方形ABCD的边长为1,其中,的圆心依次是点A,B,C.连接GB和FD,则GB与FD的关系是________.
三年模拟全练
一、选择题
1.(2019湖南长沙天心明德中学月考,3,★☆☆)下列说法中,错误的是(
)
A.半圆是弧
B.半径相等的圆是等圆
C.过圆心的线段是直径
D.直径是弦
二、填空题
2.(2019江苏淮安期中,16,★☆☆)如图24-1-1-8,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=
40°,∠OBC=50°,则∠OAC=______________°.
五年中考全练
一、选择题
1.(2018辽宁阜新中考,6,★☆☆)如图24-1-1-9,AB是⊙O的直径,点C在圆上,∠ABC=
65°,那么∠OCA的度数是(
)
A.25°
B.35°
C.15°
D.20°
二、填空题
2.(2018黑龙江龙东中考,6,★☆☆)如图24-1-1-10,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=
15°,则∠ACB=________.
核心素养全练
1.在平面直角坐标系中,⊙O的圆心为原点,点A为⊙O上一点,过点A作AB⊥x轴于B,作AC⊥y轴于C,连接BC,取BC的中点P.当点A沿圆周运动时,点P也随之运动.当点A运动到A’的位置时,点P随之运动到点P’的位置.用虚线画出点P运动的路线,下列图中,正确的是(
)
A.
B.
C.
D.
2.(独家原创试题)如图24-1-1-11,AB为半圆的直径,O为圆心,OC⊥AB交半圆于点C,点D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动.过点D作DE⊥AB,DF⊥OC,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若AB=
10.则下列关于MN的说法正确的是(
)
先变大后变小
B.先变小后变大
C.等于5
D.等于2.5
答案
基础闯关全练
1.D
圆的内部是到圆心的距离小于半径的所有点的集合,圆是到圆心的距离等于半径的所有点的集合,故到圆心的距离不大于半径的点的集合是圆的内部和圆.故选D.
2.C
∵点A与点B的距离是2
cm,即半径是2
cm,∴圆的直径是4
cm.故选C.
3.证明如图,连接ME、MD,
∵BD、CE是△ABC的高,
∴∠BEC=
∠BDC=90?,
∵M为BC的中点,
∴ME=MD=MC=MB=BC.
∴点B、C、D、E在以点M为圆心的同一个圆上.
4.A
长度相等的弧所对圆心角的度数不一定相等,只有互相重合的弧才是等弧,故A中说法错误;选项B、C、D中说法都正确,故选A.
5.C
题图中共有4条弦,分别是弦AB、弦DB、弦CB、弦CD.故选C.
能力提升全练
1.D
如图,连接OE、OD,当点O、E、D共线时,半圆片上的点D与原点O之间的距离最大,则∠AED=
∠EAO+
∠EOA,在Rt△AOB中,因为AE=
EB,所以EA=
EO=
EB,所以∠EAO=∠EOA,所以
n°=∠AED=26°.故选D.
2.C
如图,过C作CB⊥OA于点B,
∵∠COA=45?,
∴三角形BCO为等腰直角三角形.
∵OC=2.∴OB=BC=.
又∵点C位于第二象限,
∴点C的坐标为(,),故选C.
3.答案
解析
如图,作CD⊥AB于点D,连接OC,则CD=1,OD=2.在Rt△OCD中,.∴AB=
2OC=
.
4.答案
相等且互相垂直
解析
∵BC=DC,CG=
CF,
又∠FCD=
∠GCB=90°,
∴△FCD≌△GCB,
∴GB=
FD,∠G=∠F,
∴
∠G+∠CDF=∠F+∠CDF=90°,
即GB与FD的关系是相等且互相垂直.
三年模拟全练
一、选择题
1.C
过圆心的弦为直径,所以C选项的说法错误;选项A、B、D的说法都正确,故选C.
二、填空题
2.答案
30
解析
如图,连接OC,∵OC=
OB,∠OBC=50°,∴∠OCB=∠OBC=50°,
∴∠BOC=
180?-50?×2=80?,
∴∠AOB=
40°.
∴∠AOC=80°+40°=120°,∵OC=OA,
∴∠OAC=∠OCA=
30°.
五年中考全练
一、选择题
1.A
∵OB=
OC,
∠ABC=
65°,∴∠OCB=
65°,∴∠BOC=
180°-65°×2=
50°,∵AB是⊙O的直径,OA=OC,∴∠OCA=∠OAC=∠BOC=×50°=25°,故选A.
二、填空题
2.答案
60°
解析
如图,连接DC,OB,∵∠BDO=
15°,OB=OD,∴∠OBD=∠BDO=
15°,∴∠BOD=
150°.∵OD⊥AC,∴∠DOC=
90°,∴∠BOC=150°-90°=
60°,又OB=
OC,∴△BOC是等边三角形,∴∠ACB=60°.
核心素养全练
1.B连接OP,OP’,由题意可知BC=B'C'=半径,则OP=
OP’=BC,在点A的运动过程中,OP的长不变,∴点P运动的路线是以点O为圆心,OP为半径的圆的一段弧,故选B.
2.D如图,连接OD,EF,∵AB=
10,∴OD=5.∵DE⊥AB,DF⊥OC,OC⊥AB,∴四边形DEOF是矩形,∴EF=OD=5.当点D在半圆上运动时,由圆上各点到圆心的距离都等于半径,可知OD的长不变,∵点M,N分别为DE和DF的中点,∴MN=EF=OD=2.5.
/
同课章节目录
