济南历城四中2019-2020学年高中物理鲁科版选修3-4:4.1光的折射定律 达标作业(含解析)
文档属性
| 名称 | 济南历城四中2019-2020学年高中物理鲁科版选修3-4:4.1光的折射定律 达标作业(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 268.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-06 17:22:14 | ||
图片预览




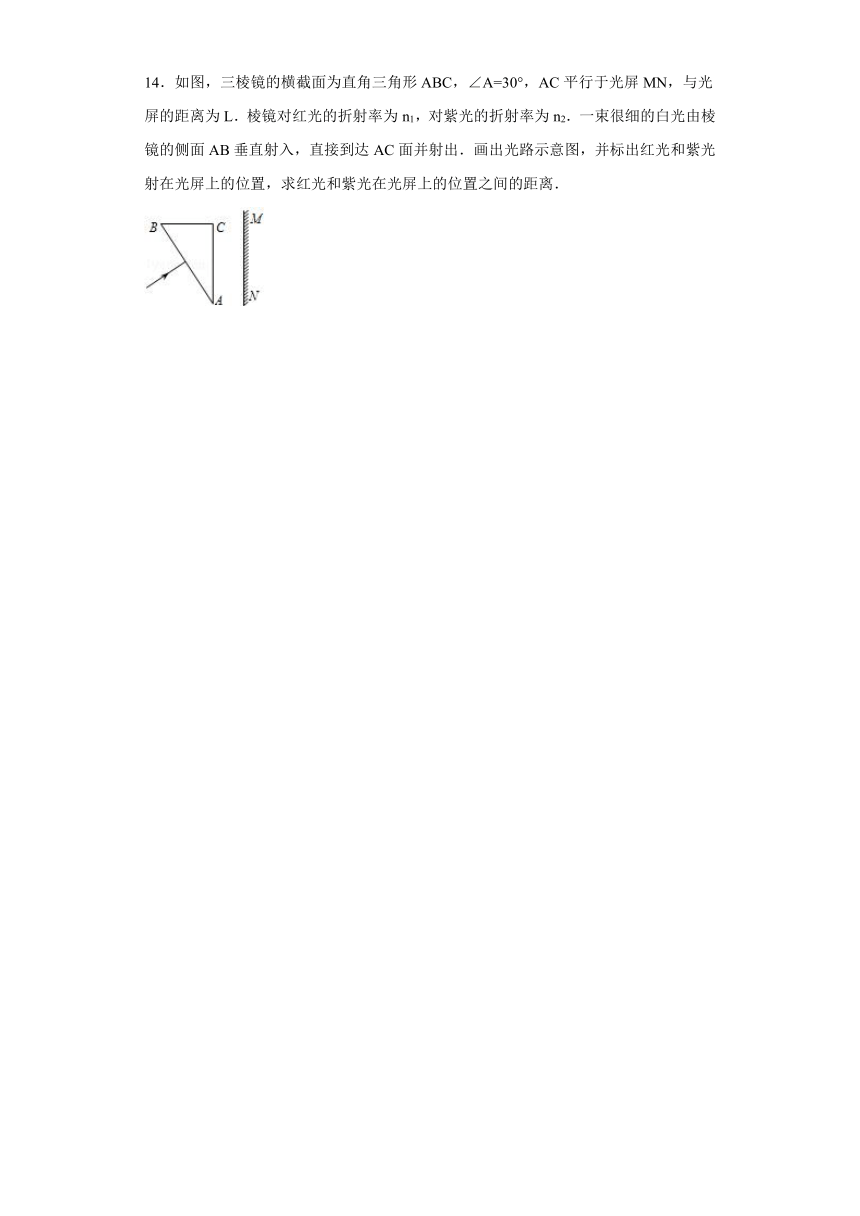
文档简介
4.1光的折射定律
1.如图所示,在空气中有一直角棱镜ABC,∠A=30°,一束单色光从AB边射入棱镜,入射角为45°,垂直于BC边射出,则该棱镜的折射率为
( )
A.
B.
C.1.5
D.
2.如图所示,等腰三角形ABC为一棱镜的横截面,顶角A为θ。一束光线从AB边入射,从AC边射出,已知入射光线与AB边的夹角和出射光线与AC边的夹角相等,入射光线与出射光线的夹角也为θ。则该棱镜的折射率为( )
A.
B.
C.
D.
3.胶囊型元件水平放置,由某透明材料制成,两端是半径为r的半球,中间是长度为4r的圆柱体,中轴线是。一激光束从左侧平行中轴线水平射入,经折射、反射再折射后又从左侧水平射出。已知出射光线与入射光线的间距为1.6r,则该元件的折射率为( )
A.
B.
C.
D.
4.如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后,变为从a、b两点射出的单色光,对于这两束单色光,下列说法错误的是(
)
A.红光在玻璃中传播速度比蓝光大
B.从a、b两点射出的单色光不平行
C.从a点射出的为红光,从b点射出的为蓝光
D.从a、b两点射出的单色光仍平行,且平行于BC
5.如图所示,一束双色光从空气射入水面,进入水中分成两束,它们与水面的夹角分别是,则两色光在水中传播速度之比为(
)
A.
B.
C.
D.
6.如图所示,P是一束含有两种单色光的光线,沿图示方向射向半圆形玻璃砖的圆心O,折射后分成a、b两束光线,则下列说法中正确的是( )
A.a光频率小于b光频率
B.在玻璃砖中传播的时间a光比b光长
C.玻璃对a光的折射率小于对b光的折射率
D.若让玻璃砖在纸面内绕O点逆时针转动180°,P光线保持不变,则a、b两束光线也保持不变
7.如图所示为一横截面为直角三角形的玻璃棱镜,其中,点在边上,、间距为,。一条光线平行于边从点射入棱镜,光线垂直边射出,已知真空中的光速为,则( )
A.玻璃对光线的折射率为
B.光线在棱镜中传播的路程为
C.光线在棱镜中传播的时间为
D.光线在棱镜中传播的时间为
8.a、b、c三条平行光线垂直于半圆柱体玻璃砖的截面直径从空气射向玻璃砖,如图所示,光线b正好过圆心O,光线a、c从光线b的两侧对称入射,从玻璃砖下表面进入空气后与光线b分别交于P、Q,则下列说法正确的是( )
A.玻璃对三种光的折射率关系为
B.玻璃对a光的折射率大于对c光的折射率
C.a光比c光穿过该半圆柱体玻璃砖所需时间长
D.a、b、c三种光穿过该半圆柱体玻璃砖所需时间b光最长
9.如图所示,两束平行的黄光射向截面ABC为正三角形的玻璃三棱镜,已知该三棱镜对该黄光的折射率为,入射光与AB界面夹角为,光经AB界面进入三棱镜后直接从BC界面射出。下列说法中正确的是( )
A.两束黄光从BC边射出后仍是平行的
B.黄光经三棱镜折射后射出方向与入射方向间的偏向角为
C.改用红光以相同的角度入射,出射光束仍然平行,但其偏向角大些
D.改用绿光以相同的角度入射,出射光束仍然平行,但其偏向角大些
E.若让入射角增大,则出射光束不平行
10.有一束单色光从介质A射入介质B,再由介质B射入介质C,如图所示。根据图中所给的情况判断,下列说法正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最大
D.光在介质C中的速度最大
11.一束光从水中射向空气,其频率将___________,波长将___________(选填“变长”或“变短”),波速将_________(选填“变大”“不变”或“变小”).
12.平行玻璃砖底面涂有反射层,一束由红光和紫光组成复合光以入射角射入玻璃砖内,其光路如图所示。则单色光a为______光;单色光______(填“a”或“b”)在玻璃中传播的时间长。
13.如图所示,ACB为半圆形玻璃砖的横截面,O为圆心,一束单色光平行于直径AB入射到圆弧上的C点,折射光线刚好可以射到B点。已知圆的半径为R,∠CBA=30°,光在真空中的传播速度为c,求:
(1)玻璃砖对该单色光的折射率;
(2)保持光的入射点位置不变,在纸面内改变入射角,使折射光线与AB的夹角为45°,则光从C点传播到AB所用的时间为多少。
14.如图,三棱镜的横截面为直角三角形ABC,∠A=30°,AC平行于光屏MN,与光屏的距离为L.棱镜对红光的折射率为n1,对紫光的折射率为n2.一束很细的白光由棱镜的侧面AB垂直射入,直接到达AC面并射出.画出光路示意图,并标出红光和紫光射在光屏上的位置,求红光和紫光在光屏上的位置之间的距离.
参考答案
1.B
【解析】
由光路图和几何知识得i′=60°,i=30°,则该棱镜的折射率为.故选B.
【点睛】解决本题的关键要灵活运用数学知识求解折射角,同时要掌握折射定律.
2.D
【解析】
根据题意画出光路图如图:
因为入射光线与AB边的夹角和出射光线与AC边的夹角相等,则
三角形为等腰三角形,DF、EF为法线,则
解得
又由几何关系得
所以
所以折射率
选项D正确,ABC错误。
故选D。
3.A
【解析】
由光路的对称性与可逆性可知,激光束在胶囊元件中的光路如下图所示。
设光线在半球处的入射角为,折射角为,则由折射定律得
由几何关系得
在三角形中,由正弦定理得
结合三角公式
联解可得
折射角
折射率
故BCD错误,A正确。
故选A。
4.B
【解析】
由n=c/v,红光的折射率较小,在玻璃中的传播速度较大,A对;折射率越大偏折程度越大,可知b点为蓝光,并且由光路图可知出射光线与入射光线平行,B错;CD对;
5.C
【解析】
设入射角为θ,根据光的折射定律可知:
所以
=
C正确,ABD错误。
故选C.
6.B
【解析】
AC.由图看出a光的偏折程度大于b光,所以根据折射定律得知:玻璃对a光的折射率大于对b光的折射率,折射率大则频率大,则a光的频率大,AC错误;
B.根据公式可知a光的折射率较大,则在玻璃砖中,a光的速度小于b光的速度,则在玻璃砖中传播的时间a光比b光长,B正确;
D.旋转前,发生折射过程是由玻璃射向空气中,而旋转180°后,发生的折射过程是由空气射向玻璃,故光线会发生变化,D错误。
故选B。
7.AC
【解析】
A.光路如下图
因为光线垂直BC边射出,有β=30°,光线在E点发生反射,有α=30°,可知r=30°,光线平行于AB边从D点射入棱镜,入射角θ=60°,由折射定律有
故A正确;
B.△ADE为等腰三角形,由几何关系有
DE=AD=L,
解得
光线在棱镜中传播的路程为
故B错误;
C
D.光线在棱镜中传播的速度
光线在棱镜中传播的时间为
故C正确,D错误。
故选AC。
8.BC
【解析】
ABD.由图可知,a光通过玻璃砖后偏折程度比c光的大,所以玻璃对a光的折射率大于对c光的折射率,即
由于玻璃对b光没有发生偏折,无法判断玻璃对b光的折射率与对a、c两光的折射率的大小。同理,也无法判断b光穿过该半圆柱体玻璃砖所需时间与另两种光的时间,故B正确,AD错误;
C.对于a、c两光,由
得
而a光传播的路程较长,所以由
可知,a光比c光穿过该半圆柱体玻璃砖所需时间长,故C正确。
故选BC。
9.ABD
【解析】
AB.如图所示,由折射率公式
n=
可得r=,由几何关系可知折射光在三棱镜内平行于底边AC,由对称性可知其在BC边射出时的出射角也为,因此光束的偏向角为,则两束光平行,故AB正确;
CD.由于同种材料对不同的色光的折射率不同,相对于黄光而言红光的折射率小,绿光的折射率较大,因此折射后绿光的偏向角大些,红光的偏向角小些,故C错误,D正确;
E.若让入射角增大,则折射角按一定的比例增大,出射光束仍然平行,故E错误。
故选ABD。
10.BC
【解析】
AB.由可知,光线由介质A进入介质B时,根据光路图可知,A的折射率大于B的折射率;光由介质B进入介质C时,根据光路图可知,B的折射率小于C的折射率,所以介质B的折射率最小;由光路的可逆性可知,光由B进入A时,如果入射角为,则折射角为;而光由B进入C时,入射角为,折射角为,由此比较可知,介质C的折射率最大;A错误,B正确;
BC.根据,得,则介质的折射率越大,光在该种介质中传播速度越小。B介质的折射率最小,则光在B介质中传播速度最大;C介质折射率最大,则光在C介质中传播速度最小,故C正确,D错误。
故选BC。
11.不变
变长
变大
【解析】
[1]由于频率取决于波源,所以一束光从水中射向空气,其频率将不变,
[2][3]光从水中射向空气波速变大,由公式可知,波长将变长。
12.紫
a
【解析】
第一空.光线进入玻璃砖时,a光的偏折程度较大,则a光的折射率较大,因此,单色光a为紫光。
第二空.设玻璃砖的厚度为d。入射角为i,折射角为r,折射率为n。则有:n=光在玻璃中的传播速度为:v=光在玻璃砖中通过的路程为:s=光在玻璃砖中的传播时间为:t=解得光在玻璃中的传播时间为:t=。采用特殊值法比较,假设a光的折射率为,b光的折射率为代入上式可得:ta:tb=:>1则ta>tb
13.(1);(2)
【解析】
(1)如图所示,根据几何关系可知,光在C点发生折射的入射角i=60°
折射角
r=30°
因此折射率
(2)如图所示,改变入射光的入射角,使折射光线CD与AB的夹角为45°,根据正弦定理有
解得
光在玻璃砖中传播的速度,则
14.红光和紫光在光屏上的位置之间的距离
【解析】
试题分析:两种色光组成的很细的光束垂直AB边射入棱镜,在AB面上不发生偏折,到达AC面上,根据几何关系求出入射角的大小,根据折射定律求出折射角,再根据几何关系求出光屏MN上两光点间的距离.
根据几何关系,光从AC面上折射时的入射角为30°,
根据折射定律有:
,
则tanr2=,tanr1=.
所以x=L(tanr2﹣tanr1)=.
点评:本题考查光的折射.关键掌握光的折射定律,以及能够灵活运用数学的几何关系.
1.如图所示,在空气中有一直角棱镜ABC,∠A=30°,一束单色光从AB边射入棱镜,入射角为45°,垂直于BC边射出,则该棱镜的折射率为
( )
A.
B.
C.1.5
D.
2.如图所示,等腰三角形ABC为一棱镜的横截面,顶角A为θ。一束光线从AB边入射,从AC边射出,已知入射光线与AB边的夹角和出射光线与AC边的夹角相等,入射光线与出射光线的夹角也为θ。则该棱镜的折射率为( )
A.
B.
C.
D.
3.胶囊型元件水平放置,由某透明材料制成,两端是半径为r的半球,中间是长度为4r的圆柱体,中轴线是。一激光束从左侧平行中轴线水平射入,经折射、反射再折射后又从左侧水平射出。已知出射光线与入射光线的间距为1.6r,则该元件的折射率为( )
A.
B.
C.
D.
4.如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后,变为从a、b两点射出的单色光,对于这两束单色光,下列说法错误的是(
)
A.红光在玻璃中传播速度比蓝光大
B.从a、b两点射出的单色光不平行
C.从a点射出的为红光,从b点射出的为蓝光
D.从a、b两点射出的单色光仍平行,且平行于BC
5.如图所示,一束双色光从空气射入水面,进入水中分成两束,它们与水面的夹角分别是,则两色光在水中传播速度之比为(
)
A.
B.
C.
D.
6.如图所示,P是一束含有两种单色光的光线,沿图示方向射向半圆形玻璃砖的圆心O,折射后分成a、b两束光线,则下列说法中正确的是( )
A.a光频率小于b光频率
B.在玻璃砖中传播的时间a光比b光长
C.玻璃对a光的折射率小于对b光的折射率
D.若让玻璃砖在纸面内绕O点逆时针转动180°,P光线保持不变,则a、b两束光线也保持不变
7.如图所示为一横截面为直角三角形的玻璃棱镜,其中,点在边上,、间距为,。一条光线平行于边从点射入棱镜,光线垂直边射出,已知真空中的光速为,则( )
A.玻璃对光线的折射率为
B.光线在棱镜中传播的路程为
C.光线在棱镜中传播的时间为
D.光线在棱镜中传播的时间为
8.a、b、c三条平行光线垂直于半圆柱体玻璃砖的截面直径从空气射向玻璃砖,如图所示,光线b正好过圆心O,光线a、c从光线b的两侧对称入射,从玻璃砖下表面进入空气后与光线b分别交于P、Q,则下列说法正确的是( )
A.玻璃对三种光的折射率关系为
B.玻璃对a光的折射率大于对c光的折射率
C.a光比c光穿过该半圆柱体玻璃砖所需时间长
D.a、b、c三种光穿过该半圆柱体玻璃砖所需时间b光最长
9.如图所示,两束平行的黄光射向截面ABC为正三角形的玻璃三棱镜,已知该三棱镜对该黄光的折射率为,入射光与AB界面夹角为,光经AB界面进入三棱镜后直接从BC界面射出。下列说法中正确的是( )
A.两束黄光从BC边射出后仍是平行的
B.黄光经三棱镜折射后射出方向与入射方向间的偏向角为
C.改用红光以相同的角度入射,出射光束仍然平行,但其偏向角大些
D.改用绿光以相同的角度入射,出射光束仍然平行,但其偏向角大些
E.若让入射角增大,则出射光束不平行
10.有一束单色光从介质A射入介质B,再由介质B射入介质C,如图所示。根据图中所给的情况判断,下列说法正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最大
D.光在介质C中的速度最大
11.一束光从水中射向空气,其频率将___________,波长将___________(选填“变长”或“变短”),波速将_________(选填“变大”“不变”或“变小”).
12.平行玻璃砖底面涂有反射层,一束由红光和紫光组成复合光以入射角射入玻璃砖内,其光路如图所示。则单色光a为______光;单色光______(填“a”或“b”)在玻璃中传播的时间长。
13.如图所示,ACB为半圆形玻璃砖的横截面,O为圆心,一束单色光平行于直径AB入射到圆弧上的C点,折射光线刚好可以射到B点。已知圆的半径为R,∠CBA=30°,光在真空中的传播速度为c,求:
(1)玻璃砖对该单色光的折射率;
(2)保持光的入射点位置不变,在纸面内改变入射角,使折射光线与AB的夹角为45°,则光从C点传播到AB所用的时间为多少。
14.如图,三棱镜的横截面为直角三角形ABC,∠A=30°,AC平行于光屏MN,与光屏的距离为L.棱镜对红光的折射率为n1,对紫光的折射率为n2.一束很细的白光由棱镜的侧面AB垂直射入,直接到达AC面并射出.画出光路示意图,并标出红光和紫光射在光屏上的位置,求红光和紫光在光屏上的位置之间的距离.
参考答案
1.B
【解析】
由光路图和几何知识得i′=60°,i=30°,则该棱镜的折射率为.故选B.
【点睛】解决本题的关键要灵活运用数学知识求解折射角,同时要掌握折射定律.
2.D
【解析】
根据题意画出光路图如图:
因为入射光线与AB边的夹角和出射光线与AC边的夹角相等,则
三角形为等腰三角形,DF、EF为法线,则
解得
又由几何关系得
所以
所以折射率
选项D正确,ABC错误。
故选D。
3.A
【解析】
由光路的对称性与可逆性可知,激光束在胶囊元件中的光路如下图所示。
设光线在半球处的入射角为,折射角为,则由折射定律得
由几何关系得
在三角形中,由正弦定理得
结合三角公式
联解可得
折射角
折射率
故BCD错误,A正确。
故选A。
4.B
【解析】
由n=c/v,红光的折射率较小,在玻璃中的传播速度较大,A对;折射率越大偏折程度越大,可知b点为蓝光,并且由光路图可知出射光线与入射光线平行,B错;CD对;
5.C
【解析】
设入射角为θ,根据光的折射定律可知:
所以
=
C正确,ABD错误。
故选C.
6.B
【解析】
AC.由图看出a光的偏折程度大于b光,所以根据折射定律得知:玻璃对a光的折射率大于对b光的折射率,折射率大则频率大,则a光的频率大,AC错误;
B.根据公式可知a光的折射率较大,则在玻璃砖中,a光的速度小于b光的速度,则在玻璃砖中传播的时间a光比b光长,B正确;
D.旋转前,发生折射过程是由玻璃射向空气中,而旋转180°后,发生的折射过程是由空气射向玻璃,故光线会发生变化,D错误。
故选B。
7.AC
【解析】
A.光路如下图
因为光线垂直BC边射出,有β=30°,光线在E点发生反射,有α=30°,可知r=30°,光线平行于AB边从D点射入棱镜,入射角θ=60°,由折射定律有
故A正确;
B.△ADE为等腰三角形,由几何关系有
DE=AD=L,
解得
光线在棱镜中传播的路程为
故B错误;
C
D.光线在棱镜中传播的速度
光线在棱镜中传播的时间为
故C正确,D错误。
故选AC。
8.BC
【解析】
ABD.由图可知,a光通过玻璃砖后偏折程度比c光的大,所以玻璃对a光的折射率大于对c光的折射率,即
由于玻璃对b光没有发生偏折,无法判断玻璃对b光的折射率与对a、c两光的折射率的大小。同理,也无法判断b光穿过该半圆柱体玻璃砖所需时间与另两种光的时间,故B正确,AD错误;
C.对于a、c两光,由
得
而a光传播的路程较长,所以由
可知,a光比c光穿过该半圆柱体玻璃砖所需时间长,故C正确。
故选BC。
9.ABD
【解析】
AB.如图所示,由折射率公式
n=
可得r=,由几何关系可知折射光在三棱镜内平行于底边AC,由对称性可知其在BC边射出时的出射角也为,因此光束的偏向角为,则两束光平行,故AB正确;
CD.由于同种材料对不同的色光的折射率不同,相对于黄光而言红光的折射率小,绿光的折射率较大,因此折射后绿光的偏向角大些,红光的偏向角小些,故C错误,D正确;
E.若让入射角增大,则折射角按一定的比例增大,出射光束仍然平行,故E错误。
故选ABD。
10.BC
【解析】
AB.由可知,光线由介质A进入介质B时,根据光路图可知,A的折射率大于B的折射率;光由介质B进入介质C时,根据光路图可知,B的折射率小于C的折射率,所以介质B的折射率最小;由光路的可逆性可知,光由B进入A时,如果入射角为,则折射角为;而光由B进入C时,入射角为,折射角为,由此比较可知,介质C的折射率最大;A错误,B正确;
BC.根据,得,则介质的折射率越大,光在该种介质中传播速度越小。B介质的折射率最小,则光在B介质中传播速度最大;C介质折射率最大,则光在C介质中传播速度最小,故C正确,D错误。
故选BC。
11.不变
变长
变大
【解析】
[1]由于频率取决于波源,所以一束光从水中射向空气,其频率将不变,
[2][3]光从水中射向空气波速变大,由公式可知,波长将变长。
12.紫
a
【解析】
第一空.光线进入玻璃砖时,a光的偏折程度较大,则a光的折射率较大,因此,单色光a为紫光。
第二空.设玻璃砖的厚度为d。入射角为i,折射角为r,折射率为n。则有:n=光在玻璃中的传播速度为:v=光在玻璃砖中通过的路程为:s=光在玻璃砖中的传播时间为:t=解得光在玻璃中的传播时间为:t=。采用特殊值法比较,假设a光的折射率为,b光的折射率为代入上式可得:ta:tb=:>1则ta>tb
13.(1);(2)
【解析】
(1)如图所示,根据几何关系可知,光在C点发生折射的入射角i=60°
折射角
r=30°
因此折射率
(2)如图所示,改变入射光的入射角,使折射光线CD与AB的夹角为45°,根据正弦定理有
解得
光在玻璃砖中传播的速度,则
14.红光和紫光在光屏上的位置之间的距离
【解析】
试题分析:两种色光组成的很细的光束垂直AB边射入棱镜,在AB面上不发生偏折,到达AC面上,根据几何关系求出入射角的大小,根据折射定律求出折射角,再根据几何关系求出光屏MN上两光点间的距离.
根据几何关系,光从AC面上折射时的入射角为30°,
根据折射定律有:
,
则tanr2=,tanr1=.
所以x=L(tanr2﹣tanr1)=.
点评:本题考查光的折射.关键掌握光的折射定律,以及能够灵活运用数学的几何关系.
同课章节目录
- 第1章 机械振动
- 导 入 从我国古代的“鱼洗”说起
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 生活中的振动
- 第2章 机械波
- 导 入 身边的波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第3章 电磁波
- 导 入 无处不在的电磁波
- 第1节 电磁波的产生
- 第2节 电磁波的发射、传播和接收
- 第3节 电磁波的应用及防护
- 专题探究 振动与波的实验与调研
- 第4章 光的折射与全反射
- 导 入 美妙的彩虹
- 第1节 光的折射定律
- 第2节 光的全反射
- 第3节 光导纤维及其应用
- 第5章 光的干涉 衍射 偏振
- 导 入 从五彩斑斓的肥皂泡说起
- 第1节 光的干涉
- 第2节 光的衍射
- 第3节 光的偏振
- 第4节 激光与全息照相
- 专题探究 光学部分的实验与调研
- 第6章 相对论与天体物理
- 导 入 从双生子佯谬谈起
- 第1节 牛顿眼中的世界
- 第2节 爱因斯坦眼中的世界
- 第3节 广义相对论初步
- 第4节 探索宇宙
