中考错题分析

(共26张PPT)
中考错题分析
数学中考中出现的错误举例：
1.计算 的结果是( )
A．—1 B．1 C．—3 D．3
1.得分率 96.2%。因不懂乘方的意义，选C的最多，占错误选项的33%。
2.得分率 85.8%。因不知基本概念，选C的最多, 占错误选项的64%。
2.使分式 有意义的x的取值范围是（ ）
A．x≠2 B. x≠-2 C．x＞-2 D．x＜2
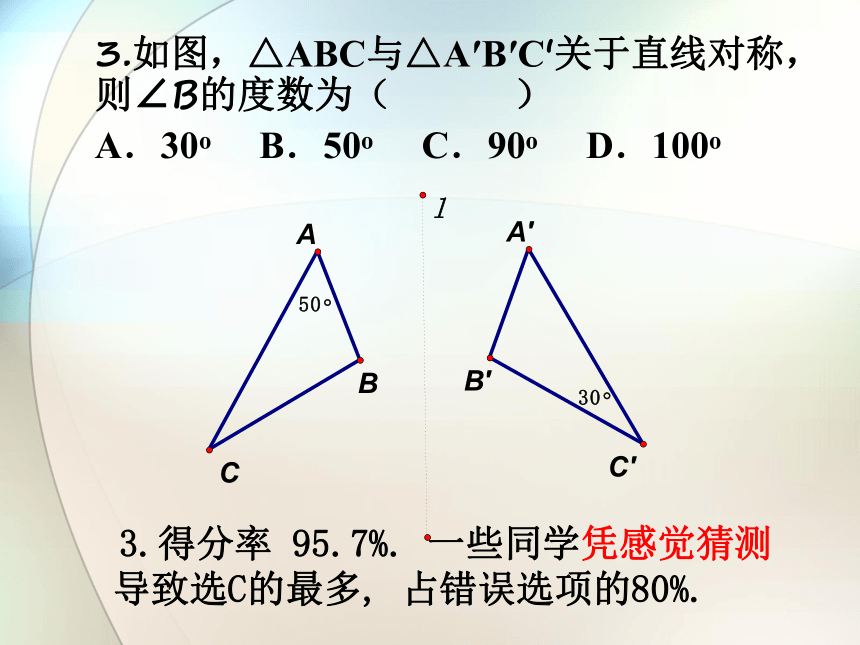
3.如图，△ABC与△A′B′C′关于直线对称，则∠B的度数为（ ）
A．30o B．50o C．90o D．100o
3.得分率 95.7%. 一些同学凭感觉猜测导致选C的最多, 占错误选项的80%.
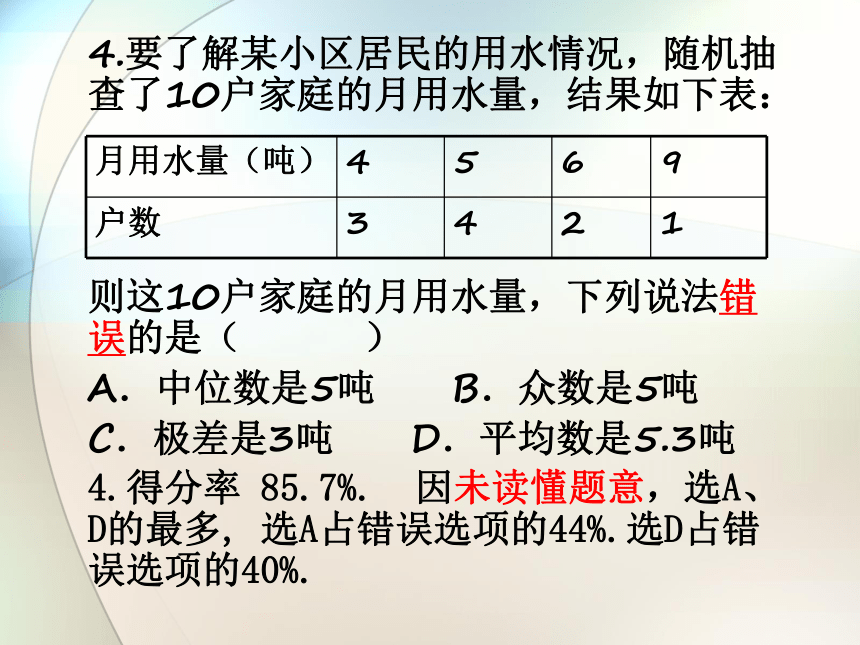
4.要了解某小区居民的用水情况，随机抽查了10户家庭的月用水量，结果如下表：
则这10户家庭的月用水量，下列说法错误的是（ ）
A．中位数是5吨 B．众数是5吨
C．极差是3吨 D．平均数是5.3吨
4.得分率 85.7%. 因未读懂题意，选A、D的最多, 选A占错误选项的44%.选D占错误选项的40%.
月用水量（吨） 4 5 6 9
户数 3 4 2 1
5．由一些大小相同的小正方体组成的几何体的俯视图如图所示，其中正方形中的数字表示在该位置上的小正方体的个数，这个几何体的左视图是（ ）
5.得分率86%. 因与主视图混淆，选B的最多, 占错误选项的78%.
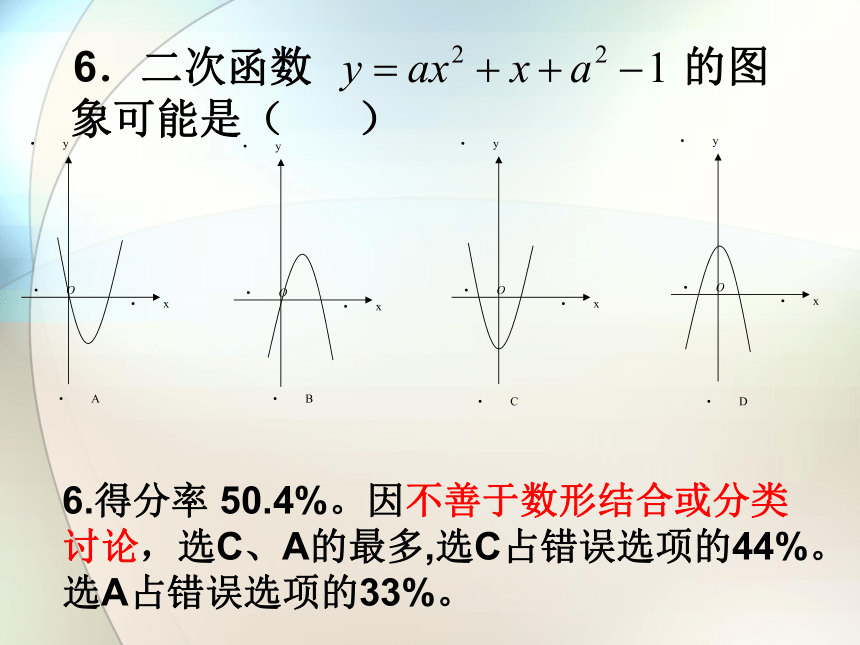
6．二次函数 的图象可能是（ ）
x
y
O
x
y
O
x
y
O
x
y
O
A
B
C
D
6.得分率 50.4%。因不善于数形结合或分类讨论，选C、A的最多,选C占错误选项的44%。选A占错误选项的33%。
7.得分率91.4%。很多同学对相反数与倒数的概念分不清，甚至一些程度很好的同学也把此题的答案写成 。
8．计算： _______.
8.得分率80%.有些是把答案的符号写错；有些是把 x的指数相乘；还出现了形如 的答案.
7． 的相反数是______________.
填空题
9．写出一个图象经过点（1，-1）的函数的表达式_____________________.
9.得分率76.3%. 因对函数图像与其解析式之间的关系不清楚。不理解 “经过点(1,-1)”。
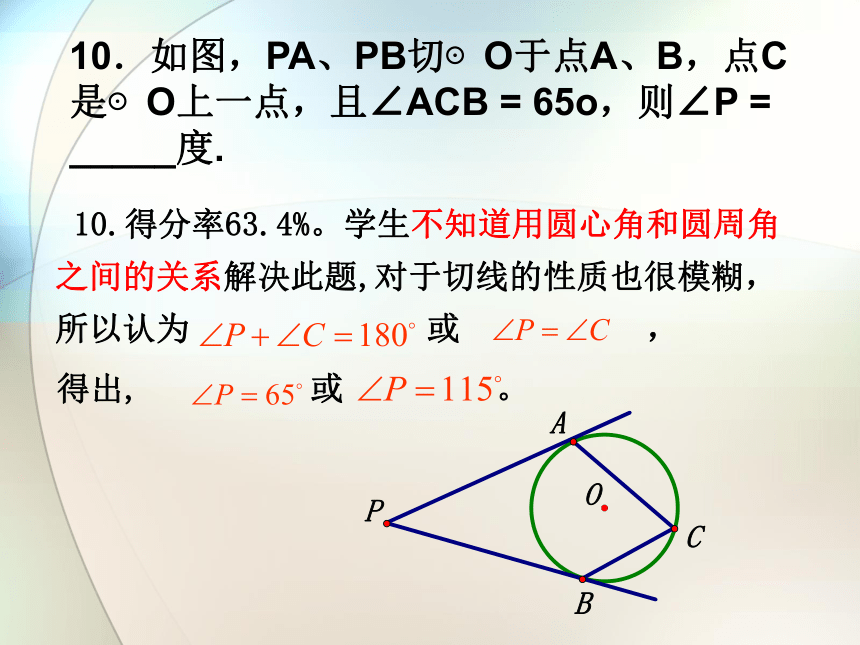
10.得分率63.4%。学生不知道用圆心角和圆周角之间的关系解决此题,对于切线的性质也很模糊，所以认为 或 ，
得出, 或 。
10．如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠ACB = 65o，则∠P = _____度.
11．如图，在直角梯形ABCD中，AB∥CD，AD⊥CD，AB = 1㎝，AD = 2㎝，CD = 4㎝，则BC = _________㎝。
11.得分率80%.不知道处理梯形问题的基本方法，不会作辅助线,还有些同学是计算错误.
12.得分率50%。出错的原因是没有写出完整答案；对于 的取值不清,未进行数形结合，忽略了0；出现了 的写法。
12．已知x为整数，且满足 ，则x = _____。
图①
图②
图③
(第13题)
……
13.将图①所示的正六边形进行进行分割得到图②，再将图②中最小的某一个正六边形按同样的方式进行分割得到图③, 再将图③中最小的某一个正六边形按同样的方式进行分割…,则第n个图形中，共有
_____个正六边形.
13.得分率48.2%。未掌握在变化之中探索规律的基本方法，有些同学是把最外边的大正六边形漏算了。
解答题
16．解方程：
16.错误分析：（1）去分母时漏乘。
（2）方法混淆
（3）去括号时漏乘
（4）移项时忘了变号
（5）忘了验根
（6）有些同学不会解分式方程.
出现错误的原因是基本知识掌握不牢固,解答格式不规范.
17．如图，点E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA的中点。 求证：△BEF≌△DGH
17.错误分析：
（1）证明过程不严谨，不写已知条件直接写出结论，或没有推理论证的过程，罗列了一大堆的已知条件后直接写出最后的结论。
(2)书写不规范比如把“≌”符号写成“ ”符号。没有将对应点的字母写在对应的位置上。
18．张彬和王华两位同学为得到一张观看足球比赛的入场券，各自设计了一种方案：
张彬：如图，设计了一个可以自由转动的转盘，随意转动转盘，当指针指向阴影区域时，张彬得到入场券；否则，王华得到入场券；
王华：将三个完全相同的小球分别标上数字1、2、3后，放入一个不透明的袋子中，从中随机取出上个小球，然后放回袋子；混合均匀后，再随机取出一个小球．若两次取出的小球上的数字之和为偶数，王华得到入场券；否则，张彬得到入场券．
请你运用所学的概率知识，
分析张彬和王华的设计方案
对双方是否公平．
18.错误分析
(1)没有用概率的知识去解决问题,比如只比较角度的大小、只分析面积大小、只用奇偶数的个数而不求概率来说明是否公平。
(2)不能准确画出表格或树状图来求概率。
(3)不仔细审题,重点放在自己去设计方案让双方公平。
19．如图，ABCD是边长为1的正方形，其中 、 、 的圆心依次是A、B、C．
（1）求点D沿三条圆弧运动到点G所经过的路线长；
（2）判断直线GB与DF的位置关系，并说明理由．
19.错误分析:
在第一问中(1)计算公式错误，弧长公式错写为“ ”“ ”“ ”。
(2)不理解“点D沿三条圆弧运动到点G所经过的路线长”的意思，认为就是三条线段的和。
(3)书写错误把 写成线段DE等。
主要原因是学生没有理解基本概念，对于一些易混的概念公式没有彻底区分开。
在第二问中(1)没有作辅助线就解答。
(2)判断直线BG和DF的位置关系错误，比如写成“BG=DF”“相交”“相切”“垂直平分”等。
(3)证明≌时方法错误,利用HL或SSA
20.错误分析
（1）不注意审题,没有按要求画图，或随手画图。
（2）做第一问求 值时不具有一般性，例如设 BC=2，BD=1，得
（3）实数的运算不彻底比如写成 等。
20．请你画出一个以BC为底边的等腰△ABC，使底
边上的高AD = BC。
（1）求tan B和sinB的值；
（2）在你所画的等腰△ABC中，假设底边BC = 5米，求腰上的高BE。
21．某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：
（1）该商场购进A、B两种商品各多少件；
（2）商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？
A B
进价（元/件） 1200 1000
售价（元/件） 1380 1200
21.错误分析:第一小题中(1)假使语言不准确例如“设A为x件,B为y件”　或“设A x件,B y件”,更有甚者“设A x,B y”。
(2)所列方程单位不统一例如等类型或在方程组中在36,6后带上单位“万”。
第二小题中(1)不能利用“使第二次经营活动获利不少于81600元”列出准确的不等式,把不少于理解成“ ”或“ ”。
(2)对打折的概念不理解,例如,设将B商品打x折,则
(3)不认真审题,把商品的总售价和总利润搞混,例如,设B种商品的售价为x元,则,其中120x 是商品的总售价。
(4)忘记答题和答中不带单位。
要总结一些习惯性的错误
1.对数的认识停留在小学阶段。
2.忽视公式成立的条件。
3.随意省略过程导致计算错误。
4.将解方程和代数式的运算混淆。
5.做题只考虑目的和个人愿望不考虑必须遵守规则。
6.懒得写必须的文字。
7.错误的迁移（如解不等式）。
8.只会机械地背诵公式中的字母而不 能用文字语言解释公式的结构特征。
9.缺乏化简意识导致的错误。
10.不做基本的检验。
11.不考虑实际问题的具体限制。
12.注意细节和结构（如：边边角）。
13. 找到一个答案后不深入思考（如：三角形的高或中垂线，弦所对的圆周角）。
14.随意增加自己想要或题目中好像有的条件。
15.仅仅凭直观就做出判断。
16.受到“假定理”的干扰。
17.画图不认真导致错误的判断。