《函数的应用》教学解读
图片预览










文档简介
(共42张PPT)
人教A版第一册第三章
《函数的应用》
教学解读
概括本章:
20个特点
21组小节
22项任务
23节课时
□
一个特点:
新增内容为主
应用单独立章
新方法新观念
体现函数价值
巩固函数概念
强调数学应用
以“方程”为核心展开,
变为以“函数”为核心展开。
两个小节:
3.1 函数与方程
3.2 函数模型及其应用
说明与建议:
1.在函数应用的教学中,教师要引导学生不断地体验函数是描述客观世界变化规律的基本数学模型,体验指数函数、对数函数等函数与现实世界的密切联系及其在刻画现实问题中的作用。
2.应注意鼓励学生运用现代教育技术学习、探索和解决问题。例如:利用计算器、计算机画出指数函数、对数函数等的图象,探索、比较它们的变化规律,研究函数的性质,求方程的近似解等。
求方程的近似解是新增加的内容,因为大量的现实问题需要求方程的近似解。
四项任务
1.函数与方程:
①结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系。
②根据具体函数的图象,能够借助计算器用二分法求相应方程的近似解,了解这种方法是求方程近似解的常用方法。
2.函数模型及其应用:
③利用计算工具,比较指数函数、对数函数以及幂函数增长差异;结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义。
④收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等)的实例,了解函数模型的广泛应用。
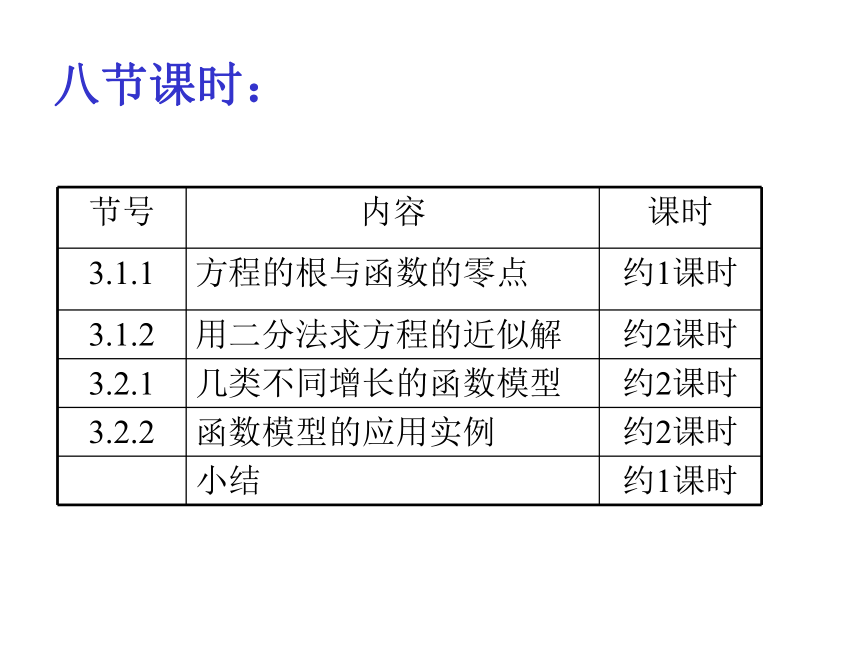
八节课时:
节号 内容 课时
3.1.1 方程的根与函数的零点 约1课时
3.1.2 用二分法求方程的近似解 约2课时
3.2.1 几类不同增长的函数模型 约2课时
3.2.2 函数模型的应用实例 约2课时
小结 约1课时
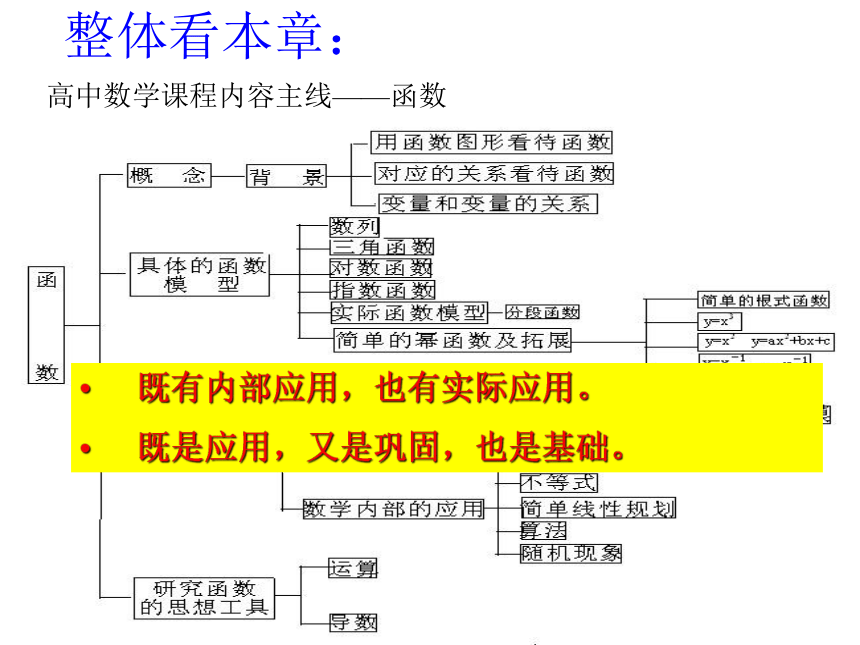
高中数学课程内容主线——函数
整体看本章:
既有内部应用,也有实际应用。
既是应用,又是巩固,也是基础。
学情分析:
初中有动手实践、自主探索与合作交流的体验
2. 初中形成的函数观
第二章形成的函数观
3. 计算机(器)普及趋势
学情分析:
4.学生基础与内部应用之间的距离
5.学生直接经验与外部应用之间的距离
6. 学生使用计算机(器)水平的不平衡
教师在教学中有着不可替代的主导作用
教学建议:
1.明确教学任务;
2.把握教学尺度;
3.凸现函数主线;
4.落实两个问题.
3.1.1方程的根与函数的零点(1课时)
基本要求:
了解函数零点的概念,了解函数零点与方程根的联系。
理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判断函数零点的个数。
具体谈教学:
3.1.1方程的根与函数的零点(1课时)
教学要点::
在思考引导下,建立函数零点概念,导出函数零点与方程根的等价关系。
在探究引导下,形成连续函数在某个区间上存在零点的判定方法。
通过动手,熟练掌握利用函数的图象和性质判断函数零点的个数的方法。
具体谈教学:
⑴
⑵
⑶
3.1.2用二分法求方程的近似解(2课时)
基本要求:
了解二分法是求方程近似解的常用方法。
能够借助信息技术工具用二分法求函数的零点或方程的近似解。
说明:
重点是通过用“二分法”求方程的近似解,使学生体会函数的零点与方程根之间的联系,初步形成用函数观点处理问题的意识。
难点是在利用“二分法”求方程的近似解的过程中,对给定精确度的近似解的计算。
具体谈教学:
教学要点:
第1课时,在思考引导下,理解二分法,认识其操作程序,并借助小结,提升二分法的价值,明确它是求方程近似解的常用方法。
第2课时,设计练习及变式,熟练掌握用二分法求函数的零点或方程的近似解的方法。
说明:
理解列表的作用;可用计算器或计算机列表;
理解解方法的两种层次要求;
掌握二分法求方程近似解的“程序”;(是一种算法)
方法类型不急于扩大,关键是掌握“二分法”。
具体谈教学:
3.1.2用二分法求方程的近似解(2课时)
教学中要注意让学生亲身体验。
在研究函数的零点与方程的根的关系、判断一个函数在某个给定区间存在零点的方法、用二分法求方程近似解的过程中渗透了函数与方程的思想;
在用二分法求函数零点的步骤、用二分法求方程近似解的过程中渗透了程序解法所蕴涵的算法思想。
具体谈教学:
3.2.1几类不同增长的函数模型(2课时)
教学要求::
理解直线上升、指数爆炸、对数增长的含义
理解指数函数、对数函数以及幂函数增长速度的差异。
能利用给定的函数模型解决实际问题;能建立确定性的函数模型解决问题;能选择适当的函数模型进行拟合实现问题解决;了解(指数函数、对数函数、幂函数、分段函数等)函数模型在社会生活中的广泛应用。
具体谈教学:
3.2.1几类不同增长的函数模型(2课时)
教学要点:
创设情景,分设四步,目的:帮助学生弄清一次函数、指数函数、对数函数以及幂函数间的增长差异,
第一步:创设一个选择投资方案的问题情景,让学生通过建模、列数表、研究函数的图象和性质,体会直线上升和指数爆炸。
第二步:创设一个选择公司奖励模型的问题情景,让学生在观察和探究的过程中,体会对数增长模型的特点。
第三步:通过三个具体函数图象、性质的探究,让学生进一步体会三种函数的增长差异,并得出一般情形:底数大于1时,指数函数的增长速度越来越快,而对数函数的增长速度越来越慢。
第四步:设置两个探究问题,让学生对幂函数和对数函数的增长差异,以及三种函数的衰减情况进行自主探究。
具体谈教学:
说明:重点是认识一、二次函数、指数函数、对数函数、幂函数模型的增长差
异,体会直线上升、指数爆炸、对数增长的差异。
难点是如何选择适当的函数模型分析和解决实际问题。
第1课时完成第一、二步;第2课时完成第三、四步。
⑴
⑵
⑶
⑷
3.2.2函数模型的应用实例(2课时)
教学要求::
初步掌握建立函数模型解决问题的基本过程和基本方法。
具体谈教学:
以函数模型的应用为主线;
针对不同的函数模型,在例题、练习、习题和复习参考题中,为学生设计了素材广泛、内容新颖的问题;(如行程问题、人口增长问题、商品定价问题、未成年人生长发育中的身高与体重问题等)
3.2.2函数模型的应用实例(2课时)
教学要点:
教学中注意贯彻:以激发学生的兴趣,开阔学生的视野,了解函数模型广泛的应用,培养学生应用意识的设计意图
说明:
通过建立函数模型以及运用模型解决问题,进一步体会函数的广泛应用及运用方法。
第1课时完成例3,例4;第2课时完成例5,例6。(各带2个练习(题))
具体谈教学:
典型案例:函数的应用举例
新教材特点:
重视应用
重视应用时学生参与
教学难度较大
目标易出偏差
对老师提出新要求
后面问题取教材: 函数应用
学生具备基础知识:
一、二次函数
幂、指、对函数
从人口统计年鉴中可查得我国从1962年至1970年人口数据资料如下表:
年份 62 63 64 65
人口(万) 67295 69172 70499 72538
66 67 68 69 70
74542 76032 78198 80700 82992
根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似的反映中国在该时间段人口数 y与年份x的函数关系?试写出这个函数模型的解析式.
教学方式变了
数学手段变了
借助Excel制作加以说明
小结(1课时)
根据学生情况;
紧扣教学目标;
再理章节结构;
突出函数主线;
熟练程序方法;
归纳提升思想;
思考:
数学课堂教学,存在着两种基本模式:
1、 演绎模式;其基本特征就是以教师为中心(即以成人社会为中心,教师作为成人社会的代表),一切从概念出发,通过定义、定理、法则、公式以及练习,强调让学生获得数学知识,形成运算技能。
2、 归纳模式;其基本特征就是以学习者为中心,一切从事实出发,即从儿童的生活经验出发,通过观察、操作、实践、思考、交流、获得结论,形成规则,强调学生对数学活动的体验,数学的再创造以及数学与生活的联系。
思考:
现代教学技术使用问题:
1. 学生会用与教师会用;
2. 展示性使用与探究性使用;
○
注意:
有限的课时(8个课时)与丰富的内容
关键:
明确教学任务,紧扣教学目标
○
计算器使用问题.
谢谢各位!
敬请指正
杭州市教育局教研室 李学军
联系电话 0571 28026021
电子信箱 lixuejun@
◇
◇
◇
◇
◇
◇
□
◇
人教A版第一册第三章
《函数的应用》
教学解读
概括本章:
20个特点
21组小节
22项任务
23节课时
□
一个特点:
新增内容为主
应用单独立章
新方法新观念
体现函数价值
巩固函数概念
强调数学应用
以“方程”为核心展开,
变为以“函数”为核心展开。
两个小节:
3.1 函数与方程
3.2 函数模型及其应用
说明与建议:
1.在函数应用的教学中,教师要引导学生不断地体验函数是描述客观世界变化规律的基本数学模型,体验指数函数、对数函数等函数与现实世界的密切联系及其在刻画现实问题中的作用。
2.应注意鼓励学生运用现代教育技术学习、探索和解决问题。例如:利用计算器、计算机画出指数函数、对数函数等的图象,探索、比较它们的变化规律,研究函数的性质,求方程的近似解等。
求方程的近似解是新增加的内容,因为大量的现实问题需要求方程的近似解。
四项任务
1.函数与方程:
①结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系。
②根据具体函数的图象,能够借助计算器用二分法求相应方程的近似解,了解这种方法是求方程近似解的常用方法。
2.函数模型及其应用:
③利用计算工具,比较指数函数、对数函数以及幂函数增长差异;结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义。
④收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数、分段函数等)的实例,了解函数模型的广泛应用。
八节课时:
节号 内容 课时
3.1.1 方程的根与函数的零点 约1课时
3.1.2 用二分法求方程的近似解 约2课时
3.2.1 几类不同增长的函数模型 约2课时
3.2.2 函数模型的应用实例 约2课时
小结 约1课时
高中数学课程内容主线——函数
整体看本章:
既有内部应用,也有实际应用。
既是应用,又是巩固,也是基础。
学情分析:
初中有动手实践、自主探索与合作交流的体验
2. 初中形成的函数观
第二章形成的函数观
3. 计算机(器)普及趋势
学情分析:
4.学生基础与内部应用之间的距离
5.学生直接经验与外部应用之间的距离
6. 学生使用计算机(器)水平的不平衡
教师在教学中有着不可替代的主导作用
教学建议:
1.明确教学任务;
2.把握教学尺度;
3.凸现函数主线;
4.落实两个问题.
3.1.1方程的根与函数的零点(1课时)
基本要求:
了解函数零点的概念,了解函数零点与方程根的联系。
理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判断函数零点的个数。
具体谈教学:
3.1.1方程的根与函数的零点(1课时)
教学要点::
在思考引导下,建立函数零点概念,导出函数零点与方程根的等价关系。
在探究引导下,形成连续函数在某个区间上存在零点的判定方法。
通过动手,熟练掌握利用函数的图象和性质判断函数零点的个数的方法。
具体谈教学:
⑴
⑵
⑶
3.1.2用二分法求方程的近似解(2课时)
基本要求:
了解二分法是求方程近似解的常用方法。
能够借助信息技术工具用二分法求函数的零点或方程的近似解。
说明:
重点是通过用“二分法”求方程的近似解,使学生体会函数的零点与方程根之间的联系,初步形成用函数观点处理问题的意识。
难点是在利用“二分法”求方程的近似解的过程中,对给定精确度的近似解的计算。
具体谈教学:
教学要点:
第1课时,在思考引导下,理解二分法,认识其操作程序,并借助小结,提升二分法的价值,明确它是求方程近似解的常用方法。
第2课时,设计练习及变式,熟练掌握用二分法求函数的零点或方程的近似解的方法。
说明:
理解列表的作用;可用计算器或计算机列表;
理解解方法的两种层次要求;
掌握二分法求方程近似解的“程序”;(是一种算法)
方法类型不急于扩大,关键是掌握“二分法”。
具体谈教学:
3.1.2用二分法求方程的近似解(2课时)
教学中要注意让学生亲身体验。
在研究函数的零点与方程的根的关系、判断一个函数在某个给定区间存在零点的方法、用二分法求方程近似解的过程中渗透了函数与方程的思想;
在用二分法求函数零点的步骤、用二分法求方程近似解的过程中渗透了程序解法所蕴涵的算法思想。
具体谈教学:
3.2.1几类不同增长的函数模型(2课时)
教学要求::
理解直线上升、指数爆炸、对数增长的含义
理解指数函数、对数函数以及幂函数增长速度的差异。
能利用给定的函数模型解决实际问题;能建立确定性的函数模型解决问题;能选择适当的函数模型进行拟合实现问题解决;了解(指数函数、对数函数、幂函数、分段函数等)函数模型在社会生活中的广泛应用。
具体谈教学:
3.2.1几类不同增长的函数模型(2课时)
教学要点:
创设情景,分设四步,目的:帮助学生弄清一次函数、指数函数、对数函数以及幂函数间的增长差异,
第一步:创设一个选择投资方案的问题情景,让学生通过建模、列数表、研究函数的图象和性质,体会直线上升和指数爆炸。
第二步:创设一个选择公司奖励模型的问题情景,让学生在观察和探究的过程中,体会对数增长模型的特点。
第三步:通过三个具体函数图象、性质的探究,让学生进一步体会三种函数的增长差异,并得出一般情形:底数大于1时,指数函数的增长速度越来越快,而对数函数的增长速度越来越慢。
第四步:设置两个探究问题,让学生对幂函数和对数函数的增长差异,以及三种函数的衰减情况进行自主探究。
具体谈教学:
说明:重点是认识一、二次函数、指数函数、对数函数、幂函数模型的增长差
异,体会直线上升、指数爆炸、对数增长的差异。
难点是如何选择适当的函数模型分析和解决实际问题。
第1课时完成第一、二步;第2课时完成第三、四步。
⑴
⑵
⑶
⑷
3.2.2函数模型的应用实例(2课时)
教学要求::
初步掌握建立函数模型解决问题的基本过程和基本方法。
具体谈教学:
以函数模型的应用为主线;
针对不同的函数模型,在例题、练习、习题和复习参考题中,为学生设计了素材广泛、内容新颖的问题;(如行程问题、人口增长问题、商品定价问题、未成年人生长发育中的身高与体重问题等)
3.2.2函数模型的应用实例(2课时)
教学要点:
教学中注意贯彻:以激发学生的兴趣,开阔学生的视野,了解函数模型广泛的应用,培养学生应用意识的设计意图
说明:
通过建立函数模型以及运用模型解决问题,进一步体会函数的广泛应用及运用方法。
第1课时完成例3,例4;第2课时完成例5,例6。(各带2个练习(题))
具体谈教学:
典型案例:函数的应用举例
新教材特点:
重视应用
重视应用时学生参与
教学难度较大
目标易出偏差
对老师提出新要求
后面问题取教材: 函数应用
学生具备基础知识:
一、二次函数
幂、指、对函数
从人口统计年鉴中可查得我国从1962年至1970年人口数据资料如下表:
年份 62 63 64 65
人口(万) 67295 69172 70499 72538
66 67 68 69 70
74542 76032 78198 80700 82992
根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似的反映中国在该时间段人口数 y与年份x的函数关系?试写出这个函数模型的解析式.
教学方式变了
数学手段变了
借助Excel制作加以说明
小结(1课时)
根据学生情况;
紧扣教学目标;
再理章节结构;
突出函数主线;
熟练程序方法;
归纳提升思想;
思考:
数学课堂教学,存在着两种基本模式:
1、 演绎模式;其基本特征就是以教师为中心(即以成人社会为中心,教师作为成人社会的代表),一切从概念出发,通过定义、定理、法则、公式以及练习,强调让学生获得数学知识,形成运算技能。
2、 归纳模式;其基本特征就是以学习者为中心,一切从事实出发,即从儿童的生活经验出发,通过观察、操作、实践、思考、交流、获得结论,形成规则,强调学生对数学活动的体验,数学的再创造以及数学与生活的联系。
思考:
现代教学技术使用问题:
1. 学生会用与教师会用;
2. 展示性使用与探究性使用;
○
注意:
有限的课时(8个课时)与丰富的内容
关键:
明确教学任务,紧扣教学目标
○
计算器使用问题.
谢谢各位!
敬请指正
杭州市教育局教研室 李学军
联系电话 0571 28026021
电子信箱 lixuejun@
◇
◇
◇
◇
◇
◇
□
◇
