人教版数学八年级下册:18.2.3 正方形的性质(19张PPT)
文档属性
| 名称 | 人教版数学八年级下册:18.2.3 正方形的性质(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 870.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-07 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
18.2.3
正方形
第一课时
人教版数学八年级下册
生活中的这些图形都给我们什么样的印象呢?
并说出它们的定义。
温故知新
18.2.3
正方形
第一课时
学习目标
1、通过观察,得出正方形的概念。知道正方形与平行四边形、矩形、菱形之间的关系。
2、类比矩形、菱形的性质,归纳出正方形的
性质,并能运用正方形的性质进行计算和证明。
(
★重点)
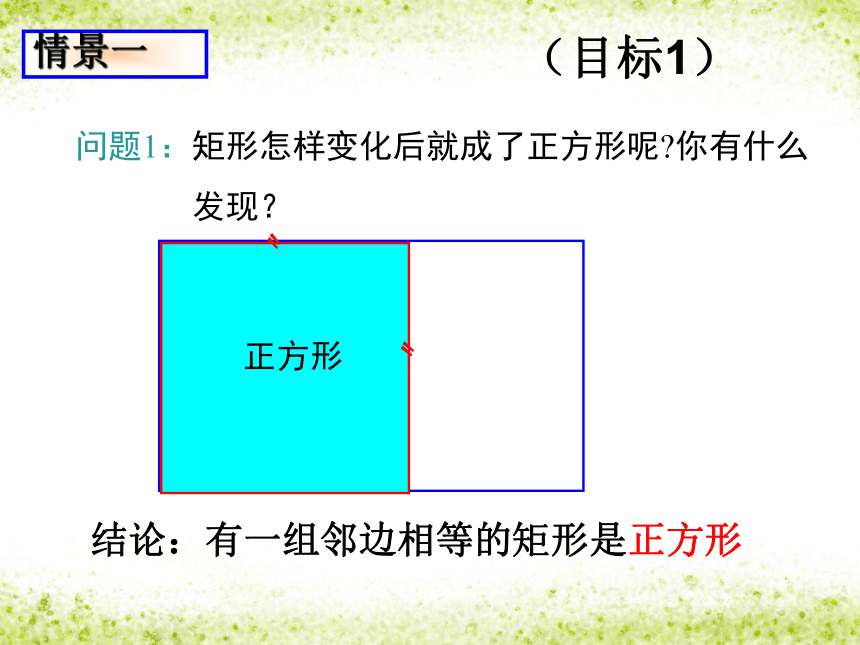
问题1:矩形怎样变化后就成了正方形呢?你有什么
发现?
情景一
(目标1)
结论:有一组邻边相等的矩形是正方形
矩
形
〃
正方形
〃
正方形
菱形
正方形
有一个角是
直角
情景二
结论:有一个角是直角的菱形是正方形
(目标1)
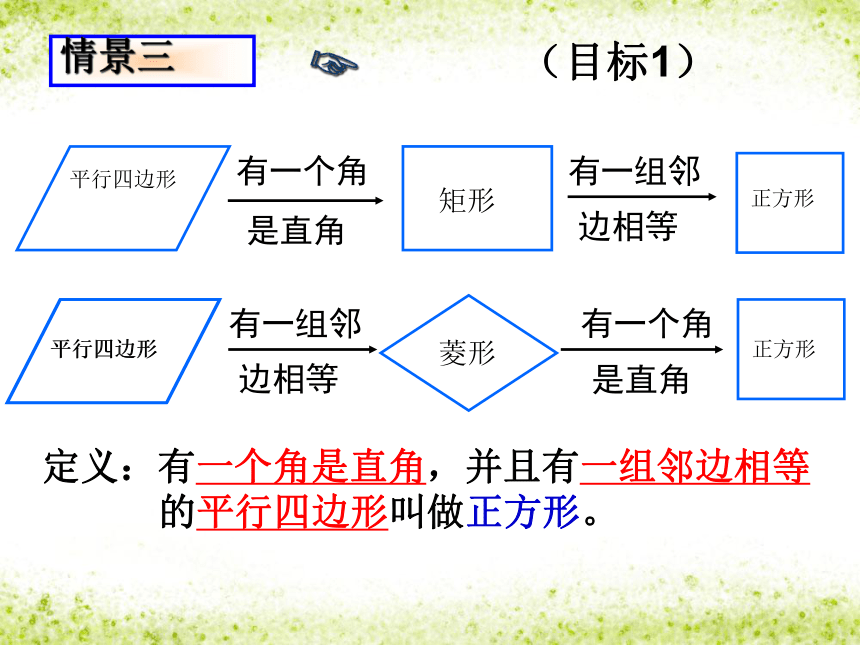
定义:有一个角是直角,并且有一组邻边相等
的平行四边形叫做正方形。
是直角
有一个角
边相等
有一组邻
是直角
有一个角
?
边相等
有一组邻
(目标1)
情景三
平行四边形
平行四边形
平行四边形
矩形
菱形
正方形
正方形
(目标1)
找关系
正方形与平行四边形,矩形,菱形之间有怎样的关系?
★
正方形是特殊的矩形
,也是特殊的菱形,
也是特殊的平行四边形
思考:
平行四边形
矩形
菱形
正
方
形
Try
your
best
判断:下列说法是否正确?为什么?
(1)
正方形一定是矩形
,正方形一定是菱形(
)
(2)
菱形一定是正方形,矩形一定是正方形
(
)
(3)
正方形、矩形、菱形都是平行四边形
(
)
(4)
四条边都相等的四边形是正方形
(
)
检测一
(达成目标1)
√
√
×
×
边
角
对
角
线
对
称
轴
矩
形
菱
形
正方形
回顾矩形和菱形的性质
,归纳出正方形的性质
对边平行
且相等
对边平行,四条边都
相等
四个角都
是直角
对角相等
邻角互补
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
2条
2条
对边平行,四条边都
相等
四个角都
是直角
对角线相等,
互相垂直平分,每条对角线平
分一组对角
4条
(目标2)
类比归纳
正方形
边
角
对角线
对称性
图形
是
图形
有
4
条对称轴
几何
文字
语言
四条边
对边
四个角
互相
每一条对角线
数学
符号
语言
∵四边形ABCD为正方形
∵四边形ABCD
为正方形
∵四边形ABCD
为正方形
A
D
B
C
A
D
B
C
A
D
B
C
都相等
平行
都是直角
平分相等且垂直
平分每一组对角
轴对称
o
合作交流
(目标2)
1
2
3
4
5
6
7
8
∴
AB∥
CD
BC
∥
AD
AB=BC=CD
=AD
∴∠A=
∠B=
∠C=
∠D=
90°
∴
AC=BD
AC⊥BD
OA=OC=OB=OD
∠1=
∠2
=
∠3
=
∠4=
∠5=
∠6
=
∠7=
∠8=
45°
1、已知正方形的一条边长为2cm,则这个正
方形的周长为
,
面积为
,
对角线长是
.
Try
your
best
检测二
(达成目标2)
8cm
2、如图,四边形ABCD为正方形,延长AB到点E,
使AE=AC,则∠BCE的度数是
.
22.5°
A
B
E
D
C
1
2
例1
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:
如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证:
△ABO、
△BCO、
△CDO、
△DAO是全等的
等腰直角三角形.
证明:∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都
是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO.
典例精析
(目标2)
例2
如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F.
试说明:AP=EF.
A
B
C
D
P
E
F
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
归纳
(达成目标2)
典例精析
已知,如图,正方形ABCD中,点E为BC上一点,AF平分∠DAE交CD于F,
求证:AE=BE+DF
拓展延伸
(达成目标2)
★从角上来谈
●从边上来谈
▲从对角线上来谈
一般
特殊
3、正方形的性质
2、几种四边形的关系
1、正方形的定义
课堂小结
有一个角是直角,并且有一组邻边相等的平行四边形叫做正方形。
必做题:
课本P59页练习题第2题,课本P62页第13题
选做题:
课本P62页习题18.2第15题
作业布置
欣赏正方形
同学们,学习之旅到此结束
同学们,学习之旅到此结束
18.2.3
正方形
第一课时
人教版数学八年级下册
生活中的这些图形都给我们什么样的印象呢?
并说出它们的定义。
温故知新
18.2.3
正方形
第一课时
学习目标
1、通过观察,得出正方形的概念。知道正方形与平行四边形、矩形、菱形之间的关系。
2、类比矩形、菱形的性质,归纳出正方形的
性质,并能运用正方形的性质进行计算和证明。
(
★重点)
问题1:矩形怎样变化后就成了正方形呢?你有什么
发现?
情景一
(目标1)
结论:有一组邻边相等的矩形是正方形
矩
形
〃
正方形
〃
正方形
菱形
正方形
有一个角是
直角
情景二
结论:有一个角是直角的菱形是正方形
(目标1)
定义:有一个角是直角,并且有一组邻边相等
的平行四边形叫做正方形。
是直角
有一个角
边相等
有一组邻
是直角
有一个角
?
边相等
有一组邻
(目标1)
情景三
平行四边形
平行四边形
平行四边形
矩形
菱形
正方形
正方形
(目标1)
找关系
正方形与平行四边形,矩形,菱形之间有怎样的关系?
★
正方形是特殊的矩形
,也是特殊的菱形,
也是特殊的平行四边形
思考:
平行四边形
矩形
菱形
正
方
形
Try
your
best
判断:下列说法是否正确?为什么?
(1)
正方形一定是矩形
,正方形一定是菱形(
)
(2)
菱形一定是正方形,矩形一定是正方形
(
)
(3)
正方形、矩形、菱形都是平行四边形
(
)
(4)
四条边都相等的四边形是正方形
(
)
检测一
(达成目标1)
√
√
×
×
边
角
对
角
线
对
称
轴
矩
形
菱
形
正方形
回顾矩形和菱形的性质
,归纳出正方形的性质
对边平行
且相等
对边平行,四条边都
相等
四个角都
是直角
对角相等
邻角互补
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
2条
2条
对边平行,四条边都
相等
四个角都
是直角
对角线相等,
互相垂直平分,每条对角线平
分一组对角
4条
(目标2)
类比归纳
正方形
边
角
对角线
对称性
图形
是
图形
有
4
条对称轴
几何
文字
语言
四条边
对边
四个角
互相
每一条对角线
数学
符号
语言
∵四边形ABCD为正方形
∵四边形ABCD
为正方形
∵四边形ABCD
为正方形
A
D
B
C
A
D
B
C
A
D
B
C
都相等
平行
都是直角
平分相等且垂直
平分每一组对角
轴对称
o
合作交流
(目标2)
1
2
3
4
5
6
7
8
∴
AB∥
CD
BC
∥
AD
AB=BC=CD
=AD
∴∠A=
∠B=
∠C=
∠D=
90°
∴
AC=BD
AC⊥BD
OA=OC=OB=OD
∠1=
∠2
=
∠3
=
∠4=
∠5=
∠6
=
∠7=
∠8=
45°
1、已知正方形的一条边长为2cm,则这个正
方形的周长为
,
面积为
,
对角线长是
.
Try
your
best
检测二
(达成目标2)
8cm
2、如图,四边形ABCD为正方形,延长AB到点E,
使AE=AC,则∠BCE的度数是
.
22.5°
A
B
E
D
C
1
2
例1
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知:
如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证:
△ABO、
△BCO、
△CDO、
△DAO是全等的
等腰直角三角形.
证明:∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都
是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO.
典例精析
(目标2)
例2
如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F.
试说明:AP=EF.
A
B
C
D
P
E
F
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
归纳
(达成目标2)
典例精析
已知,如图,正方形ABCD中,点E为BC上一点,AF平分∠DAE交CD于F,
求证:AE=BE+DF
拓展延伸
(达成目标2)
★从角上来谈
●从边上来谈
▲从对角线上来谈
一般
特殊
3、正方形的性质
2、几种四边形的关系
1、正方形的定义
课堂小结
有一个角是直角,并且有一组邻边相等的平行四边形叫做正方形。
必做题:
课本P59页练习题第2题,课本P62页第13题
选做题:
课本P62页习题18.2第15题
作业布置
欣赏正方形
同学们,学习之旅到此结束
同学们,学习之旅到此结束
